1951—2015年衢州市气象变化特征分析

2019-04-09钱子立汪颖俊程越洲陈炣欣

浙江水利科技 2019年2期

钱子立，汪颖俊，方伟，程越洲，袁斌，陈炣欣

（龙游县水利局，浙江龙游 324400）

1 问题的提出

近年来，由全球变暖引发的气候变化是目前全球关注程度最高的环境问题之一，其造成降水、气温、日照等水文要素也发生了不同程度的变化。而这些水文要素的改变势必会影响水文循环中的降水、水汽输送及蒸散发等环节，进而影响流域水资源状况[1]。国内外诸多专家学者对气候变化下水文要素的影响进行了分析与研究。郝春沣[2]等对海河流域近50 a气候要素进行趋势检验、突变点检验以及小波分析，研究探讨未来海河流域气候变化趋势。刘敏[3]等采用Mann — Kendall检验法和滑动t检验法对海河流域近50 a来水文要素的变化趋势及变异年份进行分析与讨论。李斌[4]等采用线性拟合、滑动t检验、有序聚类、Mann — Kendall法对西安市近60 a的降水量、气温等气象水文要素进行变化趋势及突变分析。章数语[5]等采用海河流域北系20个气象站1956 — 2012年降水时间序列，从趋势、周期、突变和空间差异4个方面分析该地区降水时空变化特征。董晴晴[6]等运用线性回归、Mann —Kendall检验、集中度和集中期等方法分析60 a来渭河关中地区气温和降水的变化趋势、突变特征，并探讨了变化原因。吴凯[7]等人对西辽河流域1961 — 2014年降水量年值建立由基于过程线、滑动平均、Hurst指数的初步诊断，基于相关系数、Mann — Kendall、滑动t检验、小波分析的详细诊断2部分组成的变异诊断系统。张亮亮[8]等选取1965 — 2014年辽宁省23个气象站的逐日降水量资料，利用趋势分析法、小波分析法和普通克里金空间插值法对研究去大雨与暴雨事件进行时空变化特征分析。

本文采用趋势分析、突变分析、小波分析等方法对衢州市65 a来气候趋势变化、周期变化以及突变现象进行分析，研究未来衢州市气候变化趋势，为该区域水资源规划、防洪减灾提供参考。

2 研究方法

本文选用衢州气象站气象资料，包括1951 — 2015年的日降水量，日平均气温等要素。

水文序列一般由2种或2种以上成分合成，主要分为确定性和随机性2类，确定成分具有一定的物理概念，随机成分由不规则的振荡和随机影响造成[9]。水文序列分析主要是针对确定性非周期成分中的跳跃、趋势成分以及随机性成分中的平稳独立成分的分析。

2.1 趋势分析

趋势分析是为了检验水文序列是否存在渐变的确定性规律。本文采用线性拟合法进行趋势分析，通过Spearman秩次相关检验法验证趋势的显著性。

2.2 突变分析

突变分析是为了检验水文序列是否存在跳跃的确定性规律。目前气候系统发生突变的物理机制还不甚明确，若方法使用不当，可能会得出错误结论，因此判断气候系统发生突变时，通常使用多种方法进行比较[10]。本文采用有序聚类、Lee — Heghinian检验法、Mann — Kendall检验法进行突变分析，通过对采用不同方法计算得到的结果进行对比验证。

2.2.1 有序聚类法

由有序聚类推求最可能干扰点S，其实质是求最优分割点Sn (τ)，使同类之间离差平方和最小，而类与类之间离差平方和较大。对序列xt( t =1，2，3，...，n)，设可能分割点为τ，则分割前后离差平方和为：

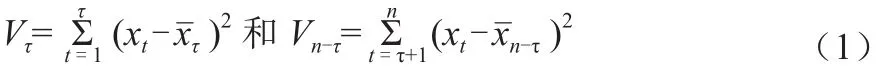
式中：

2.2.2 Lee - Heghinian检验法

Lee — Heghinian检验比较适合检验均值发生变异的情况。对序列xt( t =1，2，3，...，n)，在假定总体为正态分布和分割点τ的先验分布为均匀分布的情况下，推得可能分割点的后验条件概率密度函数为：

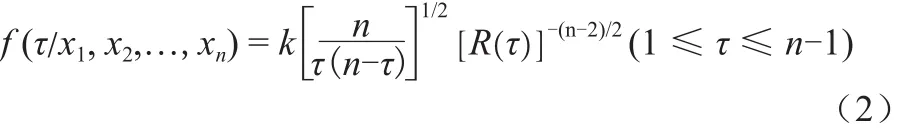
式中：k为比例常数，一般取k =1。

2.2.3 Mann - Kendall检验法

由于Mann — Kendall检验法有无需假定数据特殊分布的特点，是世界气象组织推荐处理非参数检验问题的方法，广泛适用于分析降雨、径流和蒸发等要素时间序列的变化情况[11]。

Mann — Kendall检验法能检验序列突变，定义统计变量为：

其中aij为xi＞xj(1≤j≤i )的样本累积值，定义如下：

均值E(Sk)以及方差Var(Sk)定义为：

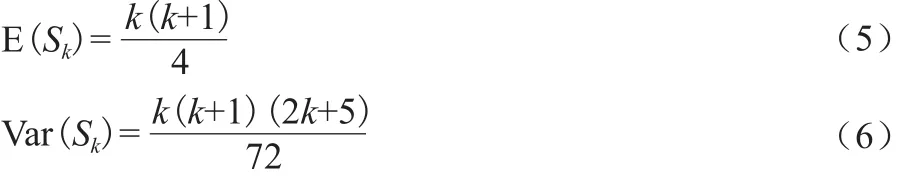
将时间序列x按降序排列，再进行计算，同时满足UBk= -UFk’且k’= n+1-k（k =1,2,... n）。通过分析统计序列UFk和UBk，不仅能分析序列x的趋势变化，还能识别突变时间，指明突变区域。若UF＞0，表示序列呈上升趋势；UF＜0则表示序列呈下降趋势；当它们超过临界直线时，表明上升或下降趋势显著。若UFk和UBk曲线出现交点，且交点位于临界直线之间，则交点所对应的时刻即为突变开始时刻。

2.3 周期分析

周期分析是为了检验水文序列是否存在周期的确定性规律。本文采用小波分析法进行分析。对于给定的小波函数ψ（t），水文时间序列f（t）的连续小波变换为∶

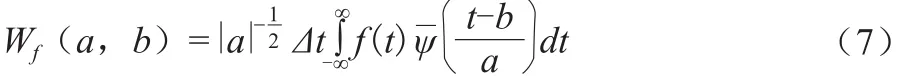
式中：a为尺度因子，反映小波的周期长度；b为时间因子，反映时间上的平移；Wf（a，b）称为小波变换系数。由于水文时间序列往往是离散的，即f（t）= f(kΔt)(k = 1，2，…，n；Δt为取样时间间隔），则f（t）的离散形式为：

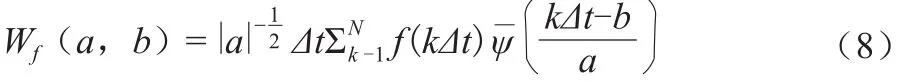
通过增加或减小伸缩尺度a来改变信号窗口大小进而得到信号的低频或高频信息，分析信号的细节，识别水文系统多时间尺度演变特征和突变特征。

3 结果分析

3.1 变化趋势分析

经分析，衢州市多年平均降雨量为1 688.1 mm，年降雨量系列极大值为1983年的2 464.5 mm，年降雨量系列极小值为1979年的1 105.7 mm，系列标准差为367.0 mm。1951 — 2015年衢州市年降雨量趋势分析见图1。图1 a为年际变化图，从图1 a中可看出衢州市65 a降水量呈增加趋势，其线性趋势方程为y = 1.172 2 x + 1 649.4，线性倾向率为1.172 2，年降雨量与时间的相关系数r为0.06。根据Spearman秩次相关检验得到，|T|＜t0.05，表明序列增加趋势不显著。

图1 b为衢州市降雨量年内变化图。从图1 b中可看出衢州市降雨量年内分布极不均匀，呈正偏态分布。10、11、12、1月的降雨百分比为1.0% ～ 5.0%，2、7、8、9月的降雨百分比为5.0% ～ 10.0%，3、4、5、6月的降雨百分比为10.0% ～ 20.0%。降雨主要集中在5月、6月，其次为4月、3月，分别占到18.2%，15.0%，12.2%，11.1%。

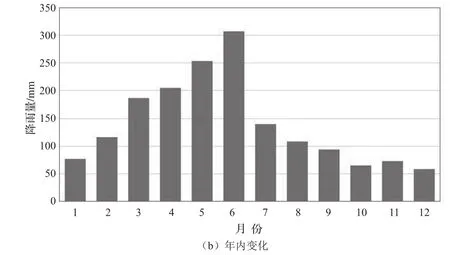
图1 1951—2015年衢州市年降雨量趋势分析图

1951 — 2015年衢州市年平均气温趋势分析见图2。经分析，衢州市多年平均气温为17.4 ℃，年气温系列极大值为1998、2007年的18.5 ℃，年气温系列极小值为1984年的16.6 ℃，系列标准差为0.4 ℃。图2 a为年际变化图，从图2 a中可以看出，衢州市65 a气温呈增加趋势，其线性趋势方程为y = 0.012 4 x +17.022，线性倾向率为0.012 4，年降雨量与时间的相关系数r为0.53。根据Spearman秩次相关检验得到，|T |≥t0.05，表明序列上升趋势显著。

图2 b为气温年内变化图。从图2 b中可看出1951 —2015年衢州市气温年内分布较均匀，呈正态分布。

图2 1951—2015年衢州市年平均气温趋势分析图

3.2 突变分析

1951 — 2015年衢州市年降雨量突变分析见图3。图3 a为衢州市年降雨序列离差平方和Sn(τ)曲线图。由图3 a可知：2013年对应的Sn(τ)为整个序列最小值，为最可能的变异点。1955年，2009年对应的Sn(τ)为局部最小值，也可能是变异点。图3 b为衢州市年降雨序列条件概率密度函数f(τ/x1,x2,...,xn)曲线图。由图3 b可知：2013年对应的f(τ/x1,x2,...,xn)为整个序列最大值，为最可能的变异点。1955年，2009年对应的f(τ/x1,x2,...,xn)为局部最大值，也可能是变异点。

图3 c为衢州市年降雨量Mann — Kendall统计量曲线。由图3 c可知：20世纪50年代末期到90年代中期，降雨量呈减少趋势；20世纪90年代到21世纪初期，降雨量呈增加趋势；21世纪初期后半段，降雨量呈减少趋势。在20世纪90年代，2条曲线有一个交点。根据 UF 和 UB 这2条曲线交点的位置，发生在 1955年左右。

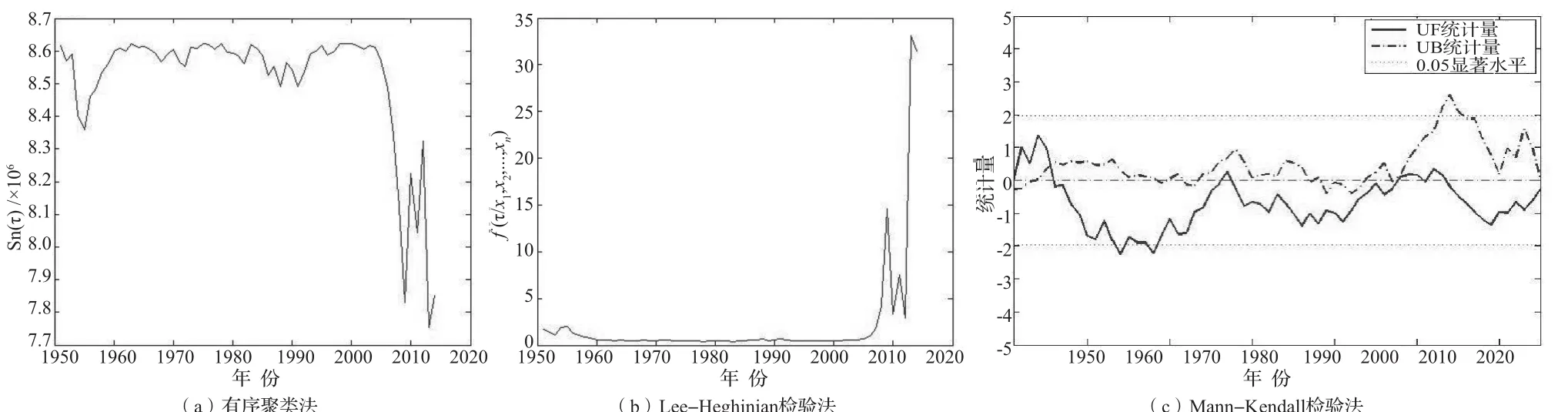
图3 1951 — 2015年衢州市年降雨量突变分析图

1951 — 2015年衢州市年平均气温突变分析见图4。图4 a为衢州市年平均气温序列离差平方和Sn(τ)曲线图。由图4 a可知：1997年对应的Sn(τ)为整个序列最小值，为最可能的变异点。1958年，2012年对应的Sn(τ)为局部最小值，也可能是变异点。图4 b为衢州市年平均气温序列条件概率密度函数f(τ/x1,x2,...,xn)曲线图。由图4 b可知：1997 年对应的R(τ)为整个序列最大值，为最可能的变异点。

图4 c为衢州市年平均气温Mann — Kendall统计量曲线图。由图4 c可知：20世纪60年代到80年代初期，气温呈现增加的趋势；20世纪80年代到90年代末期，气温呈减少趋势；20世纪90年代末期，气温呈现明显的增加趋势。特别是2003年以来，这种增加的趋势大大的超过显著性水平0.05的临界线。这些表明衢州市气温近 10 多年增加的趋势十分显著。在 20世纪90年代，2条曲线有一个交点。根据 UF 和 UB 这2条曲线交点的位置，发生在1997年左右。

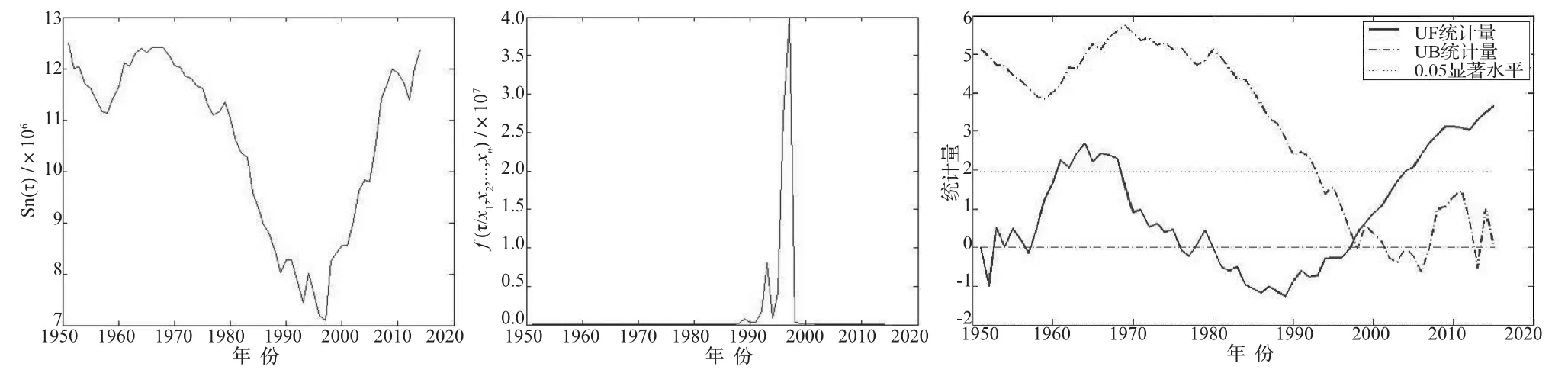
图4 1951 — 2015年衢州市年平均气温突变分析图

3.3 周期分析

根据小波分析理论，小波系数的实部表示不同特征时间尺度信号在不同时间的强弱和位相两方面的信息，而模（平方）的大小表示特征时间尺度信号的强弱。

图5为1951 — 2015年衢州市年降雨量周期分析图。由图5 a可知，65 a衢州市年降水量年际变化周期以32 ～ 34 a时间尺度信号最强，主要发生在 1951 — 1962 年、2004 —2015 年、1986 — 1991 年以及 1995 — 2003 年，振荡中心分别为 1951，2015，1989年，1998年。另外，56 ～ 57 a周期在1951 — 1958年、2005 — 2015期间信号较强。由图5 b可知，年降雨存在12，34，56 a周期，其中主周期是34 a。由图5 c可知，34 a对应的周期也比较明显，年降水量分为4个丰水期和3个枯水期，在1951 — 1955年、1968 — 1978年、1990 — 2003年以及2013年以后等4个时段为正相位，表明降水偏多，处于丰水期；在1956 — 1971年、1980 —1986年以及1997 — 2004年等4个时段为负相位，表明降水偏少，处于枯水期；其突变点分别为1955，1968，1978，1990，2003，2013年。由图5 d可知，34 a特征时间尺度小波实部过程线存在4个丰枯变化期，能发现丰水期降雨量呈上升趋势，枯水期降雨量呈平稳趋势。经相位分析，2013年以后年降雨量存在一个正相位，意味着未来5 ～ 10 a时间年降雨量将处于丰水期。建议出台应对暴雨台风应急措施，通过加强工程巡查频率、水土流失监测以及城市防洪排涝等工作排除安全隐患，提高危患意识。

图5 1951 — 2015年衢州市年降雨量周期分析图

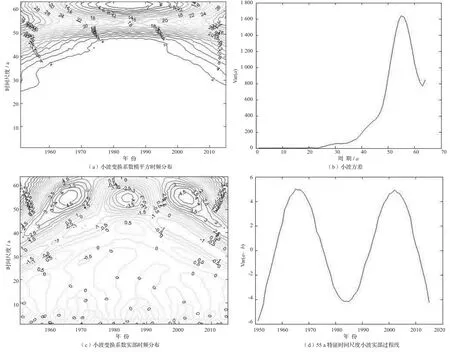
图6 1951 — 2015年衢州市年平均气温周期分析

图6为1951 — 2015年衢州市年平均气温周期分析图。由图6 a可知，65 a衢州市年平均气温年际变化周期以55 ～ 57 a时间尺度信号最强，主要发生在 1951 — 1960年、2008 — 2015 年，振荡中心分别为 1951、2015年。由图6 b可知，年平均气温存在55 a周期，其中主周期是55 a。由图6 c可知，55 a对应的周期也比较明显，年平均气温分为2个偏高期和3个偏低期，在1951 — 1955年、1975 — 1997年以及2008年之后等3个时段为负相位，表明气温偏低；在1956 — 1975年以及1997 — 2008年等2个时段为正相位，表明气温偏高；其突变点分别为1955，1975，1997，2008年。由图6 d可知，55 a特征时间尺度小波实部过程线存在3个高低变化期，能发现正相位年平均气温呈平稳趋势，负相位年平均气温呈上升趋势。经相位分析，2008年以后年平均气温存在一个负相位，意味着未来10 ～ 20 a时间年平均气温将处于偏低期。建议出台工程质量检测措施，通过加强混凝土防冻措施、绿化植物防霜冻等工作提高工程质量。