基于最优矢跨比的拱形大巷拱高设计数值模拟研究

薛 帅

（晋城煤业集团赵庄煤业 ，山西 晋城 048000）

拱形断面具有减小应力集中、提高断面利用率、减小掘进工程量等诸多优势，尤其是在复杂地质条件下应用更为广泛。但矿井在设计拱形断面时，多从满足巷道基本功能的角度出发，对巷道断面形式引起的应力分布等问题考虑较少，设计缺乏科学依据，导致巷道维护状况不佳。并且现在多数支护设计都是在巷道断面确定之后，属于滞后设计，未能充分发挥巷道断面本身的支护作用[1～2]。拱形断面巷道矢跨比为设计时最重要的因素，为矢高与跨径之比。因此，针对赵庄煤业三盘区巷道断面进行研究，分析不同矢跨比条件下，围岩应力、塑性区等分布情况，为断面设计提供理论依据。

1 工程概况

赵庄煤业三盘区有三条盘区大巷，均布置在煤层中，服务年限约10年。原始设计采用矩形断面，由于埋深超过750m，地应力作用明显，且煤质酥软、构造复杂、采动影响频繁，大巷变形严重，平均每年返修1～2次，返修方式多为挑顶、扩帮、起底之后，重新进行喷浆和锚杆索支护。随着返修次数增多，赵庄煤业认识到巷道断面设计重要性，为增强巷道围岩自身承载能力，拟将巷道断面设计成直墙拱形。

大巷顶底板岩性见表1所示。

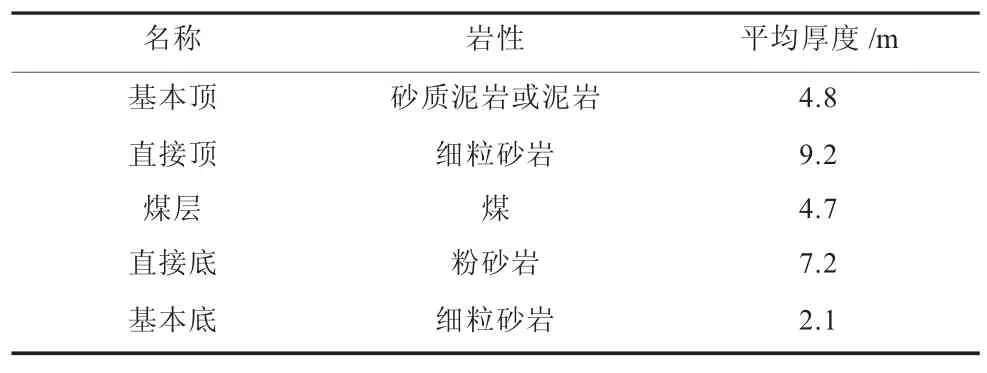
表1 顶底板岩性表

2 数值模型建立

固定直墙高度2m，跨度5.5m，根据工程实际赋予各岩层参数，分别建立巷道矢跨比为0（矩形）、0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.45、0.50时数值计算模型，部分模型如图1所示。

图1 部分不同矢跨比数值计算模型

3 运算结果及数据分析

3.1 围岩应力分布

不同矢跨比条件下，经过运算得到巷道围岩垂直应力和水平应力分布云图，部分结果见图2所示。

图2 部分不同矢跨比数值计算模型

不同矢跨比条件下，帮部不同深度围岩垂直应力分布情况见图3所示。

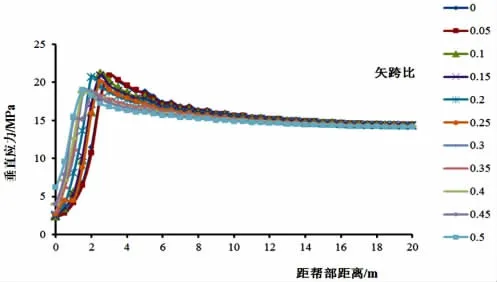
图3 不同矢跨比巷道帮部围岩垂直应力分布

由图2和图3可以看出，巷道断面由矩形变化到半圆拱形，围岩垂直应力与水平应力峰值均向巷道浅部转移。矢跨比在0～0.3之间，随矢跨比增大，垂直应力峰值注浆向巷帮浅部围岩转移，且应力集中系数有所下降，但矢跨比由0.3到0.5变化过程中，应力集中系数减小不明显。

3.2 塑性区分布

不同矢跨比条件下，经过运算得到巷道围岩塑性区分布图，部分结果见图4所示。

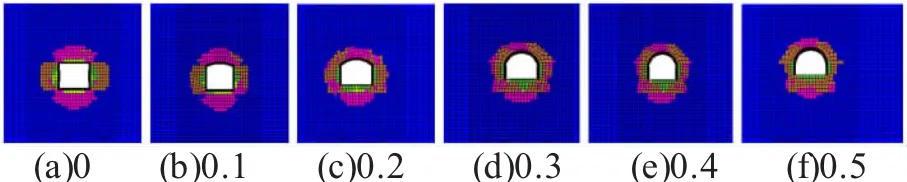
图4 部分不同矢跨比塑性区分布图

由图4可以看出，矢跨比在0～0.3之间，随矢跨比增大，巷道顶帮围岩塑性区范围有减小趋势，但矢跨比由0.3到0.5变化过程中，顶板和两帮围岩塑性区变化不大，但底板围岩塑性区范围略有增大，这主要是由于在两帮压模效应和水平应力作用下，容易引起底鼓。

3.3 顶板下沉量

不同矢跨比条件下，巷道顶板不同深处顶板下沉量如图5（a）所示，巷道顶板同一深度不同矢跨比条件下围岩下沉量对比结果量如图5（b）所示。

由图5可以看出，矢跨比在0～0.3之间，随矢跨比增大，顶板围岩位移量逐渐减小，巷道顶板下沉量主要集中在0～3m范围内；巷道顶板下沉量在矢跨比为0.3时出现拐点，变化速率逐渐降低，说明巷道矢跨比达到0.3后，再提高矢跨比，巷道顶板下沉量减小不再明显。

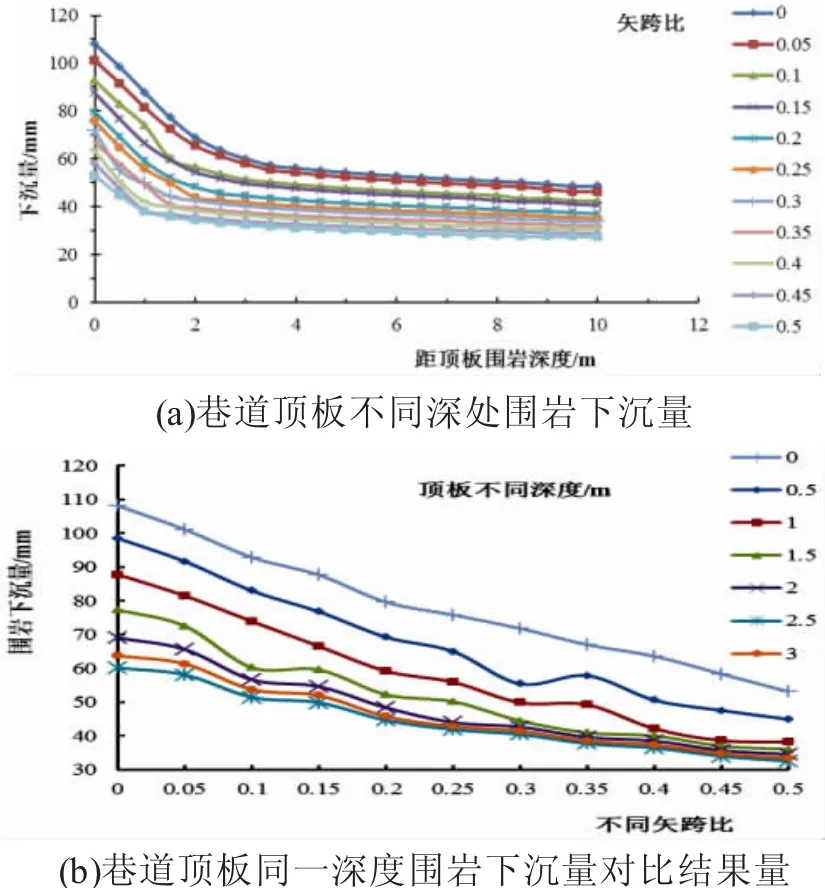
图5 顶板位移变化曲线

根据上述研究，最优矢跨比为0.3，因此初始设计拱高为1.65m。

4 结论

1）拱形断面大巷拱高设计应得到足够的重视，矢跨比为最重要设计因素；

2）建立不同矢跨比下数值计算模型，研究围岩应力分布、塑性区分布、顶板下沉量三个因素；

3）计算结果表明，矢跨比在0～0.3时，随矢跨比增大，围岩应力、塑性区和顶板下沉量减小明显，矢跨比在0.3～0.5时，随矢跨比增大，变化速率明显下降且底鼓有增大区域，因此以0.3作为最优矢跨比，初始设计拱高为1.65m。