爆破载荷下隧道围岩破坏裂隙范围研究❋

费鸿禄 苏 强 蒋安俊 洪陈超

辽宁工程技术大学爆破技术研究院(辽宁阜新，123000)

引言

钻爆法是隧道施工常用方法之一，爆破施工过程中对周围岩体的扰动和破坏过程一直是备受关注的问题。专家学者对此展开了一系列研究，冷振东等[1]通过建立一个四分区损伤范围模型对预测钻孔爆破粉碎区范围的改进模型进行了研究；胡荣等[2]采用PMMA材料制试样，通过改变裂纹与炮孔的角度对爆破载荷作用下裂纹的扩展规律进行了研究；韩森等[3]采用超声波测试和岩石压缩试验方法，从爆破前、后岩体平均波速和岩石平均抗压强度两个方面研究了白云岩岩体的爆破损伤；林英松等[4]通过分析数据建立考虑惯性矩的模型，从动力学的角度，研究了爆生气体作用下孔壁岩石的开裂机理；杨小林等[5]以断裂力学理论为支撑，通过模拟煤体爆破试验，研究了应力波和爆生气体作用下裂纹扩展长度和破碎原因。尽管专家们已经对裂隙范围有了突破性进展，但在冲击波作用后，爆生气体应该是充满粉碎区，前人们只考虑爆生气体充满炮孔，而没考虑充满粉碎区。

本文中，在考虑粉碎区范围、应力波衰减指数改变和岩石三向受力状态而不考虑初始损伤和地应力的前提下，对粉碎区、裂隙区范围进行计算。在爆生气体充满粉碎区后，通过岩石的断裂韧性来确定裂隙的二次扩展范围。采用理论推导与现场试验相对比的方法，对爆破载荷下隧道围岩的裂隙范围进行研究。对于合理确定爆破参数、分析围岩的稳定性、合理制定安全加固措施、确定隧道围岩的裂隙范围等显得尤为重要。

1 爆炸产生的荷载计算

按声学近似原理求解爆炸瞬间炸药在炮孔壁上产生的冲击波压力。若采用耦合装药[6-7]:

式中:p为冲击波压力，MPa；p0为炸药爆轰压力，MPa；ρ为岩石密度，kg/m3；ρ0为炸药密度，kg/m3；Cp为岩石纵波速度，m/s；D为炸药爆速，m/s；γ为爆轰产物的膨胀绝热指数，一般凝聚炸药取γ＝3。

若采用径向不耦合装药，不耦合系数k较小时，爆生气体的膨胀只经过p0＞pk这一种状态[8]，pk为炸药的临界压力，Pa，对于2＃岩石乳化炸药，pk为200 MPa。岩石中的透射冲击波压力为[9]

式中:k为装药径向不耦合系数，k＝rc/rb，rb、rc分别为装药半径和炮孔半径，mm；n为炸药爆炸产物膨胀炮孔壁时的压力值增大系数，一般取n＝10。

冲击波在岩体内传播的过程中逐渐衰减为应力波。岩体中任意一点的径向应力和切向应力可表示为[7]

式中:σr为径向应力，MPa；σθ为切向应力，MPa；为比例距离为计算点到炮孔中心的距离，mm；α为冲击波衰减指数时，取α＝3，为应力波衰减指数时，取α＝2－μd/(1－μd)，μd为岩石的动态泊松比；b为侧向压力系数，b＝μd/(1－μd)。有研究表明[10]，在隧道围岩爆破的加载率范围内，μd＝0.8μ，μ为岩石的静态泊松比。

2 粉碎区范围计算

冲击波作用范围内，岩体处于体积压缩状态，取其中任一单元体进行分析[11]，如图1。图1中，β为岩体两组共轭破坏面与σr的夹角。

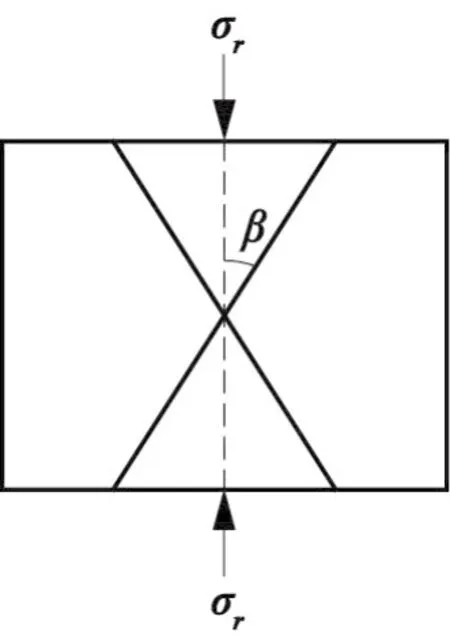
图1 单元体受力图Fig.1 Element force diagram

按摩尔-库伦破坏准则，岩体在压缩应力作用下表现为沿剪切面的剪切破坏，这与实际岩体表现出的破坏形式一致，因此，采用摩尔-库伦破坏准则判断岩体破坏与否是合适的。由一点的应力状态分析可得破坏面上的正应力和剪应力分别为

式中:σβ为破坏面上的正应力，MPa；τβ为破坏面上的剪应力，MPa。σr由式(4)确定。

摩尔-库伦岩石破坏条件为

式中:φ、c分别为岩石的内摩擦角和黏聚力系数。

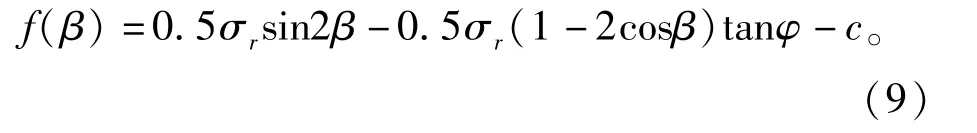
岩石发生破坏时，f(β)必然取得最大值，则有下式成立:

将式(9)代入式(10)得

将式(6)、式(7)、式(11)代入式(8)中，得压碎区内岩石的破坏条件为

粉碎区范围为

式中:R1为粉碎区范围的半径，mm。

3 裂隙区范围计算

材料的实际受力情况和性质决定了它在外载荷作用下的破坏准则[12]。由于岩石属于脆性材料，岩石的抗压强度比抗拉强度大很多。已有专家[6，13]证明在岩石爆破中，岩石处于三向应力状态，岩石受压破坏形成粉碎区，受拉破坏形成裂隙区。

如果将该问题看成平面应变问题，则可以得到

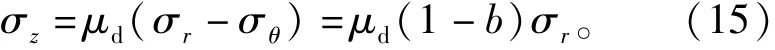
岩石中任一点的应力强度[9]为

将式(4)、式(5)、式(15)代入式(16)，可得

破坏条件为

式中:σi为裂隙区岩石任意一点的应力强度，MPa；σtd为岩石的单轴动态抗拉强度，MPa。

有关研究表明[7]，岩石的动态抗拉强度与静态抗拉强度在爆破加载应变范围内的关系为

式中:σt为岩石的静态抗拉强度，MPa。

粉碎区外就是裂隙区，由式(4)、式(14)、式(18)可计算出裂隙区的范围:

式中:B＝[(1＋b)2－2μd(1－b)2(1－μd)＋(1＋b2)]1/2；α为应力波衰减指数，α＝2－μd/(1－μd)；σL为粉碎区和裂隙区临界面上岩石的径向应力，MPa；R2为裂隙区范围的半径，mm。

4 爆生气体作用下裂隙二次扩展范围计算

爆生气体以准静态压力的形式作用于应力波形成的裂隙区，并以膨胀、挤压、气楔等综合作用使径向裂隙产生二次扩展。炸药爆轰完毕，爆生气体迅速膨胀，假定整个过程是等熵绝热的，当时，爆生气体的膨胀规律为[14-15]

式中:p1为爆生气体膨胀过程中的瞬时压力，MPa；ρx为爆生气体膨胀过程中的瞬时密度，kg/m3；A为常数。

假定爆生气体在炮孔中的膨胀规律遵循式(21)，则充满炮孔后爆生气体多的压力为

4.1 裂隙扩展的平均宽度

由一维爆生气体膨胀理论可知，爆生气体在粉碎区的压力随时间变化的关系为式中:t为时间，s；x为爆生气体沿炮孔轴向运动的距离，m；C0为爆生气体的声速，m/s。C0按式(24)确定:

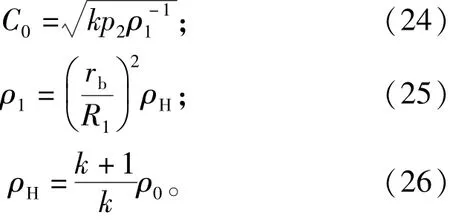
式中:ρ1为爆生气体充满粉碎区时的密度，kg/m3；ρH为爆生气体的初始密度，kg/m3。

裂隙扩展速度极限值为[14]

式中:A为常数，A＝0.27Lb，Lb为炮孔长度，m。由裂隙扩展的极限速度Vm＝0.38Cp[16]，可得裂隙扩展过程中的平均宽度为

4.2 起裂和止裂

假定爆生气体致裂时粉碎区范围不变，其膨胀压力为

式中:γ为绝热指数，γ＝1.4；a为裂隙随爆生气体压力变化的扩展长度，mm。

由断裂力学理论可知，如果岩石的断裂韧性小于裂隙尖端的应力强度因子，就会起裂，反之就会止裂。断裂力学模型如图2，裂隙尖端的强度因子可表示为[17]

图2 断裂力学模型Fig.2 Fracture mechanics model

式中:F是与裂隙区半径和裂隙长度有关的系数，取值与(R1＋a)/R1有关，随着裂隙长度的增大而增大，当(R1＋a)/R1＞1.5时，F→1.0。

裂隙尖端的应力强度因子在起裂前可表示为

式中:KIC为岩石的断裂韧性，MPa·m1/2。

采用刘军等[18]的方法对岩石的断裂韧性进行计算。

由裂隙扩展条件KI＞KIC，可得初始起裂条件为

裂隙扩展的临界驱动力为

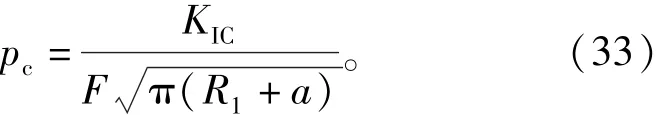
式中:pc为临界驱动力，MPa。

如果爆生气体压力与临界驱动力满足p2＞pc，裂隙就会扩展。但爆生气体压力会随着裂隙的扩展逐渐降低，当p2＜pc时，裂隙停止扩展。

4.3 裂隙二次扩展的长度计算

根据止裂条件，考虑到裂隙尖端止裂时R1＋a/R1远大于1.5，即F➝1，故裂隙停止扩展时:

式中:pm为止裂时爆生气体的压力，MPa；am为止裂时裂隙扩展的长度，mm。

同时，pm和am满足式(29):

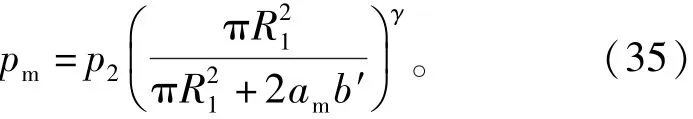
联立式(34)、式(35)，可求解不考虑爆生气体损失情况下裂隙二次扩展的最终长度。

5 工程实例及现场试验

以福建省福州市福平铁路新鼓山隧道爆破开挖为工程依托，对爆破载荷作用下隧道围岩的损伤情况进行研究。新鼓山隧道穿越福州市鼓山，进口位于福州市东山村东侧，出口位于福州市魁岐村北侧。隧道设计为单洞双线，总长8 199 m，起止里程为DK5＋095～DK13＋294。

5.1 隧道围岩物理参数

在现场选取与声波试验相同的岩样[19]，做巴西劈裂试验，如图3，测岩体的抗拉强度，试验获得的数据如表1，隧道围岩炸药和炮孔计算参数如表2。

图3 劈裂后试件Fig.3 Post split specimen

表1 劈裂抗拉试验数据Tab.1 Splitting tensile test data

对表1试验的抗拉强度取平均值，得到试件的平均抗拉强度约为10.19 MPa。

5.2 现场试验

本次现场试验过程中，上台阶爆破作用下掌子面的循环进尺为2.5 m，现场具体的炮眼布置情况如图4，炸药类型为2＃岩石乳化炸药。爆破参数如表3。现场采用楔形掏槽，单段最大药量为28.8 kg。从表3中可以看出，爆破过程中共选取8个段别的导爆管，采用毫秒导爆管延时起爆。

表2 隧道围岩炸药和炮孔计算参数Tab.2 Tunnel surrounding rock explosives and calculation parameters of blasting holes

5.3 计算结果分析

新鼓山隧道属于大断面隧道，周边眼采用不耦合装药。由于周边眼的作用是控制隧道断面规格形状，因此，理论计算时选取周边眼作为研究对象。按照现场爆破试验的参数并结合隧道围岩的实际情况，用表1、表2中的参数对爆破载荷作用下隧道围岩的裂隙范围进行计算。通过式(2)～式(14)计算，可得粉碎区的半径R1＝2.97rb＝47.52 mm；按式(15)～式(20)计算，应力波作用下岩体的裂隙范围R2＝15.14rb＝242.24 mm。哈努卡耶夫[20]的研究表明，炸药在岩石中爆炸时形成的粉碎区半径为装药半径的2～3倍，裂隙圈半径为装药半径的10～15倍，故该方法是可靠的。联立式(34)、式(35)，则不考虑爆生气体损失的情况下爆生气体对岩体二次扩展范围理论计算值为am＝856.37 mm，岩石的裂隙范围为1 098.61 mm。

图4 爆破方案炮眼布置图Fig.4 Arrangement scheme of blasting holes

表3 台阶法上台阶断面爆破参数Tab.3 Blasting parameters of the upper step section in bench method

NM-4A非金属超声检测分析仪将电信号转换为超声波信号，从发射探头传入被测围岩，将接收探头收到的声波信号转为电信号进行处理，并传输给收集系统。通过分析监测到的声波速度的变化情况，确定围岩在爆破载荷作用下的裂隙范围。由于拱顶处无法向声波孔内注水，所以只对侧周边眼的裂隙范围进行声波试验，声波孔现场布置如图5，现场测试如图6。

图5 声波孔现场布置Fig.5 The site layout of acoustic hole

图6 现场测试Fig.6 Field test

现场通过NM-4A非金属超声检测分析仪，测得在爆破载荷作用下掌子面附近岩体的损伤范围为1.2～1.4 m。通过对比可知，理论计算值比实测值小8.45%，是由于未考虑初始损伤和掘进爆破对隧道围岩造成一定程度的损伤。通过以上分析，该计算方法可以对岩石裂隙范围进行估算。

6 结论

冲击波作用下岩石的粉碎区半径为炮孔半径的2.97倍，在考虑粉碎区的情况下，计算出应力波作用下岩石的裂隙区范围为242.24 mm。

考虑粉碎区和裂隙区存在的情况下，把爆生气体充满炮孔修改为充满粉碎区，用岩石的断裂韧性来计算爆生气体对岩石裂隙造成的二次扩展范围，更具有合理性。从而求得不考虑爆生气体损失情况下，裂隙二次扩展的长度为856.37 mm。

理论得出的围岩裂隙范围比现场采用声波法所测得的围岩裂隙范围小8.45%，其原因可能与掘进爆破对隧道围岩造成一定程度初始损伤，且为群孔爆破有关，该计算方法可以对类似工况的隧道围岩裂隙范围进行估算。