基于CATIA的乘用车前驱动轴布置优化

张伟 陈忠廷 于霞 李林

（中国第一汽车股份有限公司天津技术开发分公司）

作为整车的重要关键部件，驱动轴起到连接变速箱与车轮的作用，其功能是保证等速、可靠、平稳、低噪声地将发动机的动力传递给车轮，同时满足汽车行驶过程中车轮上跳、下跳、转向等多种工况轴的伸缩与摆动的要求[1]。合理的驱动轴布置方案可以将行驶过程中产生的附加载荷、振动噪声、运动行程控制在允许的范围内，同时降低整车各工况下出现共振及干涉现象的风险[2]。文章基于某款EV 车型的前悬架运动机构，利用CATIA 软件建立模型，从总成布置角度、移动节滑移范围、空间位置校核等方面对驱动轴布置方案进行优化，旨在通过合理的驱动轴布置，使整车能够在最大程度上发挥传动效率，提高NVH 性能，为汽车传动系统提供稳定而高效的动力输出。

1 驱动轴总成结构及布置形式

图1示出驱动轴总成结构简图。

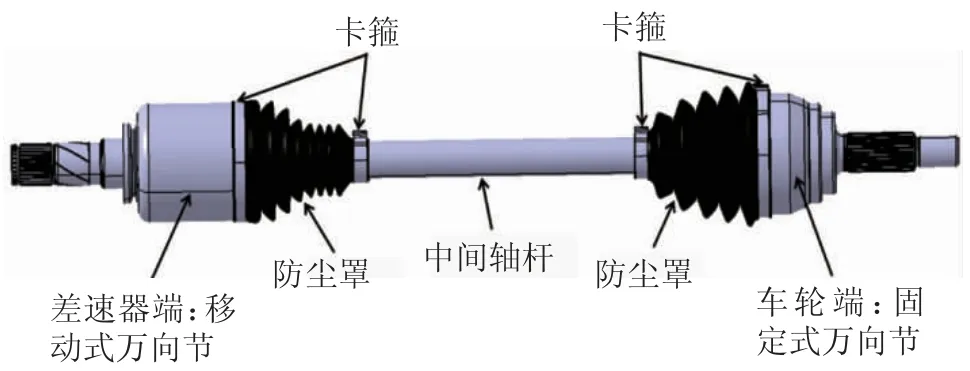
图1 驱动轴总成结构简图

驱动轴总成在整车上的布置形式需根据机舱布置、动力总成倾角、轴杆长度、直径、轴间夹角及相位、轮毂点坐标等参数进行确定。这些参数直接影响到驱动轴移动式万向节工作时的角度变化量和轴向滑移变化量。角度变化越大，万向节磨损越严重，会影响万向节的使用寿命；轴向滑移设计变化量越小，对于动力传动越理想，驱动轴的NVH 性能也好些，同时还可以减少轮胎的非正常磨损[2]。因此，要求万向节的初始角度和变化范围尽量小（设计载荷状态下，初始角度应控制在7°以下）。

驱动轴总成的布置形式主要分为两轴式和三轴式，如图2所示。两轴式布置形式结构简单、成本低，在传统经济型轿车中被广泛采用，但因装配后移动节壳体靠近差速器，所以需在差速器端口处预留足够大的布置空间，且左右轴杆长度不一致，增加了跑偏风险；三轴式布置形式需在长轴一侧移动端节柄处增加中间支撑结构，用以改善差速器端口处的布置空间，同时左右中间轴杆长度更趋于一致，提高了刚度一致性，降低了跑偏风险。

图2 驱动轴总成布置形式

文章基于某款EV 车型进行分析，考虑到电机在起步阶段输出扭矩值较大，对左右轴杆扭转刚度一致性要求较高，故采用三轴式布置形式。

2 建立DMU运动学模型

2.1 空间机构自由度计算

由于受零件结构等因素的影响，模型搭建容易出现错误，与实际运动不符，不能达到运动仿真分析的目的，所以仿真前需对模型进行详细分析，并通过系统自由度的计算，确保模型搭建的正确性。

采用机构运动学方法建立悬架系统模型，需要满足式（1）所示的系统自由度[3]。

式中：N——行驶系统运动部件数量；

fi——各运动副约束自由度数量；

FD——行驶系统驱动自由度数量。

2.2 DMU运动学模型建立

将所开发前轴系统三维模型导入CATIA 软件，构建系统零部件及运动副拓扑关系，如图3 所示，图3 中括号内数字为对应运动副约束自由度。

图3 汽车零部件及运动副拓扑关系示意图

依次搭建前轴系统DMU 模型，如图4所示。

图4 汽车前轴系统DMU 模型图

模型共包含运动部件16 个（系统自由度数为96，其中车身安装点为固定部件），运动副21 个（约束自由度数为94）。按照车型悬架及转向行程设计要求，在车轮轮胎接地点处施加轮跳驱动（驱动自由度数为1）、在转向器齿条处施加转向驱动（驱动自由度数为1），所建立DMU 模型满足式（1）。

3 DMU运动学特性仿真分析

3.1 仿真试验设计

在CATIA 中对麦弗逊前悬架仿真模型进行双轮同向跳动仿真试验。根据动力总成位置及姿态、前悬硬点参数、车轮定位参数、车轮上下跳行程、转向行程等输入条件，建立前轴系统DMU 运动学模型。

3.2 滑移摆角分析

根据建立的设计载荷状态下的DMU 运动模型，初步确定驱动轴轴杆长度。经测量，驱动轴理论内、外节心点的距离为474.4 mm。依据此轴杆长度、移动节极限滑移曲线、车轮上下跳行程及转向行程等输入条件，进行驱动轴滑移摆角分析。

经测量，驱动轴在以下9 种工况中的滑移、摆角参数，如表1 和图5所示。向内滑移为负，向外滑移为正。

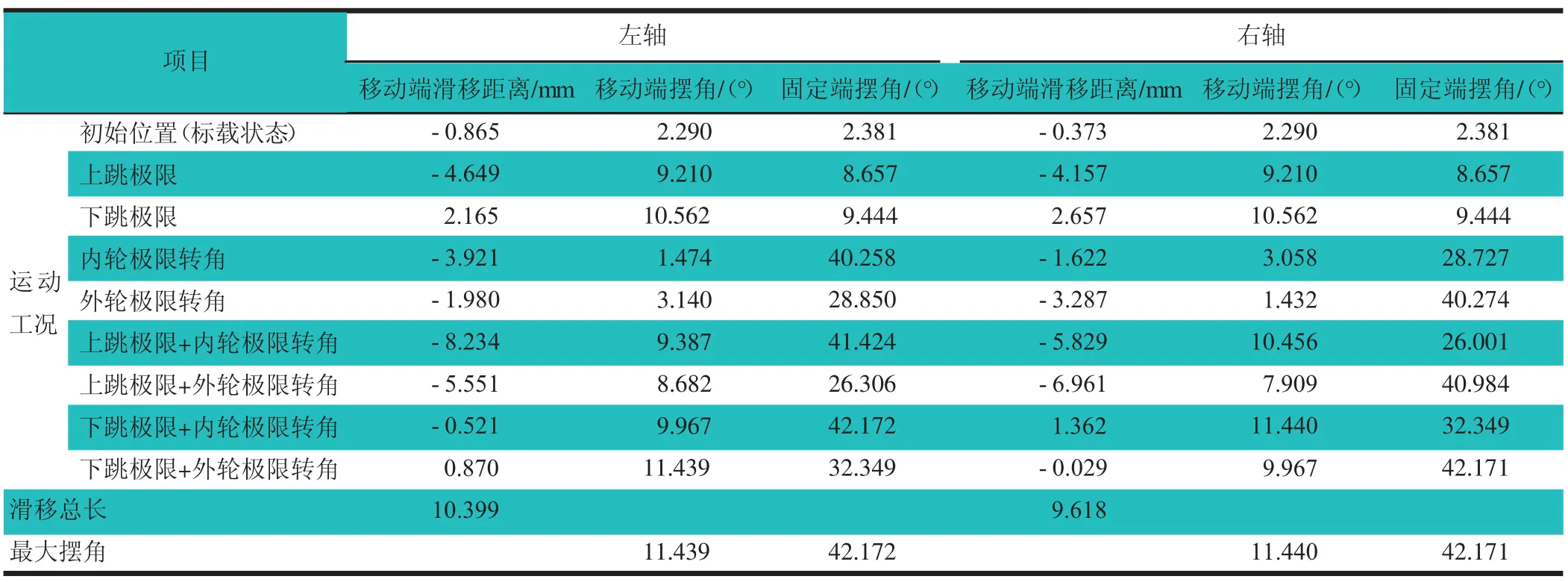
表1 驱动轴端节滑移及摆角参数（优化前）

图5 驱动轴移动节滑移摆角曲线图（优化前）

从表1 可以看出：左轴节心点向内滑移最大约为8.2 mm，向外滑移最大约为2.2 mm，移动节最大摆角为11.4°，固定节最大摆角为42.2°；右轴向内滑移最大约为7.0 mm，向外滑移最大约为2.7 mm，移动节最大摆角为11.4°，固定节最大摆角为42.2°。

从图5 可以看出，节心点的轨迹大部分分布在中心点内侧，且在“上跳极限+极限转角”工况，节心点超出“安全曲线”范围，存在“磕碰”风险。故将轴杆长度优化为473 mm后进行验证，验证结果，如表2 和图6所示。

表2 驱动轴端节滑移及摆角参数（优化后）

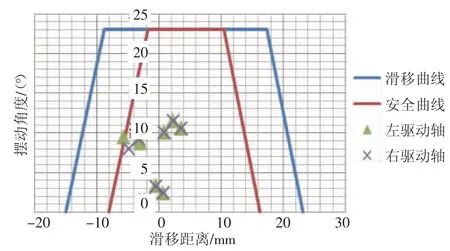
图6 驱动轴移动节滑移摆角曲线图（优化后）

从表2 可以看出，在标载整车位置，驱动轴移动节最大摆角为2.359°，固定节最大摆角为2.512°。在9 种运动工况下，左轴节心点向内滑移最大约为5.6 mm，向外滑移最大约为3.6 mm，移动节最大摆角约为11.5°，固定节最大摆角约为42.2°；右轴向内滑移最大约为4.8 mm，向外滑移最大约为3.6 mm，移动节最大摆角为11.5°，固定节最大摆角为42.2°。

万向节两端夹角相近，标载静止时不大于4°，驱动轴总成可获得较好的NVH 性能和传动效率，降低振动噪声风险。

从图6 可以看出，节心点的轨迹大部分分布在中心点两侧，且在9 种工况下，节心点未超出“安全曲线”范围，“磕碰”及“脱出”风险较小。

3.3 空间位置分析

根据建立的设计载荷状态下的DMU 运动模型，在车轮上下跳及转向过程中，动态监测驱动轴与周边部件的位置间隙。根据整车运动部件布置要求，需保证最小间隙≥10 mm。

通过CATIA 软件输出DMU 运动行程中驱动轴与各部件的间隙值，因左、右驱动轴轴杆长度一致，且左右前轴系统采用对称布置，故仅分析一侧运动间隙即可，分析结果如图7所示。下跳为负，上跳为正。

图7 驱动轴与周边部件空间位置间隙图

从图7 可以看出，在DMU 运动模型中优化后的驱动轴与周边部件的空间位置间隙均大于“允许最小间隙值”。综合滑移摆角及空间位置分析结果，此方案达到了较为理想的设计要求。

4 结论

文章基于CATIA 软件，建立前轴系统的DMU 运动学模型，并运用此模型进行驱动轴滑移摆角、空间位置分析，快速高效地进行方案优化。通过优化得出：优化后轴杆长度满足基本的运动学要求，同时降低万向结构部件与移动节内腔的干涉风险，起到了在设计初期识别并有效降低潜在风险的作用，为实车验证阶段提供了数据参考。合理的驱动轴布置，可以提高驱动轴总成的NVH 性能、传动效率，并为汽车传动系统提供稳定而高效的动力输出。在本课题中，由于不存在运动过程中驱动轴与周边部件干涉的情况，针对此方面问题的优化方案还需进一步深入探究。