无解线性方程组的一题多解方法

符和满

（肇庆学院 数学与统计学院，广东 肇庆 526061）

1 问题提出

已知数域P上的线性方程组

其中,a1,a2,a3,a4互不相等.证明该方程组无解.

此问题可见于文献[1].下面从多个角度探讨其证明过程.

2 方法探讨

2.1 运用消元法求解

消元法是求解线性方程组最常用的方法.我们可以使用消元法证明一个线性方程组无解.首先用初等变换将线性方程组化为阶梯形方程组，把最后的一些恒等式“0=0”（如果出现的话）去掉.如果剩下的方程中最后1个等式是零等于1个非零的数，则方程组无解[2]111.当然，这些初等变换过程也可以通过矩阵形式完成.即对增广矩阵作初等行变换，化成阶梯形矩阵.若阶梯形矩阵的最后1个非零行的末位元素非零，而该行的其余元素为0，则原方程组无解.

证 因为a1,a2,a3,a4互不相等，所以aj-ai≠0,其中1≤i＜j≤4.

由阶梯形矩阵的最后1行可知，出现了矛盾方程“0=1”，所以原方程组无解.

2.2 运用线性方程组有解判别定理求解

定理1[2]137线性方程组AX=b有解的充分必要条件是系数矩阵A与增广矩阵有相同的秩,其中=(Ab).

定理1提供了判别线性方程组无解的最直接方法,即一个线性方程组无解当且仅当其系数矩阵与增广矩阵不等秩.由此将问题归结为判别系数矩阵的秩与增广矩阵的秩不相等.

因为

以及a1,a2,a3,a4互不相等，所以但系数矩阵 A是个 4×3矩阵，显然秩(A)≤3，因此秩(A)≠秩根据定理1，可知该方程组无解.

2.3 转化为齐次线性方程组求解

通过引入一个“额外”变量，将非齐次线性方程组转化为齐次线性方程组.然后借助齐次线性方程组的相关结论进行证明.

定理2[3]53设A是数域P的1个n级方阵.齐次线性方程组AX=0只有零解,当且仅当系数矩阵的行列式|A|≠0.

证 假设原方程组有解，设为(c1,c2,c3)，则(c1,c2,c3,-1)就是齐次线性方程组（1）的1个非零解.

当a1,a2,a3,a4互不相等时，齐次线性方程组（1）的系数矩阵的行列式

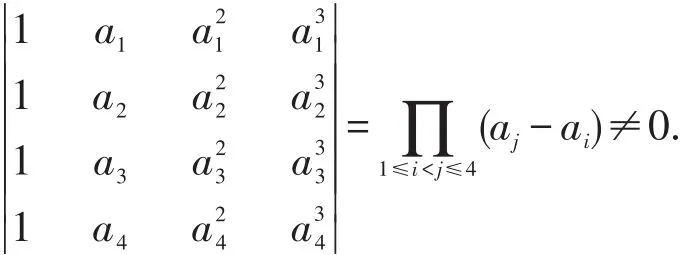
由定理2，上述的齐次线性方程组（1）只有零解,矛盾.因而原方程组无解.

2.4 转化为一元多项式求解

基于本问题中线性方程组的系数与常数项的特殊性，若将“变量”与“系数”的地位反转，则原方程组有解可视为多项式f(t)=x1+x2t+x3t2-t3有4个根a1,a2,a3,a4.为了采用多项式证明原问题，需要应用多项式理论中的1个基本结论.

定理3[2]25数域P上的n次多项式(n≥0)在数域P中的根不可能多于n个，重根按重数计算.

证 考虑数域P上关于t的一元多项式f(t)=x1+x2t+x3t2-t3.

倘若原方程组有解，则a1,a2,a3,a4是多项式f(t)的4个互异的根；但注意到多项式f(t)的次数为3，由定理3可知，3次多项式不可能有4个互异的根，所以原方程组无解.

3 问题推广

一般地，此问题还可以推广到n个变量的情形.已知数域P上的线性方程组

其中,a1,a2,…,an+1互不相等.证明该方程组无解.

同理，运用上述的各种方法进行证明，此处不再赘述.