挡风玻璃三维形貌测量系统的设计*

于 振，于万成，王桂莲

(1.天津大学 精密仪器与光电子工程学院，天津 300072；2.青岛工贸职业学校，山东 青岛 266041；3.山东省轻工工程学校，山东 青岛 266100)

0 引言

挡风玻璃是构成车身的重要附件，现在加工中常将玻璃通过真空和吹气吸附到压模表面，然后让压模下降，使其和冷却风栅贴合，冷却后得到的钢化玻璃[1]。用这样的工艺生产出来的玻璃常因为表面不平整而导致光学畸变的发生[2]。光学畸变的存在会影响司机开车时对周边事物的观察，甚至可能导致车祸等残局的发生[3]。为了减少光学畸变，需要设计一种高精度的非接触测量方法来定量的分析玻璃形面，从而指导对玻璃压膜的调整。目前国外的一些公司已经生产出可用于玻璃检测的设备，但大多价格昂贵。而国内尚未生产出有能够较好的检测玻璃光学畸变部位三维形貌的专用设备。

双目视觉被广泛应用于三维检测、机器人导航、医学成像等领域[4]。目前研究主要集中在摄像机标定[5-6]特征匹配[7-8]及精度分析[9]等方面。为了提高测量精度，很多专家学者更是将研究重点放在了特征匹配部分，提出了如快速双边滤波算法[10]、基于自适应权重的三边滤波算法[11]、迭代优化的自适应权重算法[12]以及二进制立体匹配算法BSM等方法[13]。本文立足于双目立体视觉理论，提出了一种对汽车挡风玻璃三维形貌进行测量的方法。测量中先投影黑色背景下有序排列的两列白色方块，然后用斑块提取算法提取斑块中心相面坐标，最后经过排序和匹配，求出斑块中心在相机坐标系(世界坐标系)下的三维坐标，通过坐标变换，转化为玻璃坐标系下的坐标。测量系统不移动的情况下，通过程序控制，让每次投影的白色方块都和前几次投影的在不同的位置。通过多次投影、斑块提取和匹配，逐渐实现整个视场范围内挡风玻璃表面的扫描测量。多次移动测量系统和坐标变换，可逐渐获得整个挡风玻璃表面在玻璃坐标系下的坐标。通过改变白色方块的大小和排列顺序，可以改变测量点的密集程度。实验表明该方法能够实现对挡风玻璃表面三维形貌的精确测量。

1 系统结构参数设计

通常情况下，左右摄像机对称布置，且各项参数比较接近，测量系统x和y方向上的测量误差大致相同[14]，在分析系统测量误差时可只考虑X轴方向和Z轴方向误差，系统测量误差可表示为：

(1)

由此可得，各结构参数对精度影响的分析模型如图1所示。图中α和β分别表示相机的视角和相机主光轴与Z轴间的夹角，通常情况下β>α。fl和fr分别表示左右相机的焦距(fl=fr=f)，B表示两相机间的距离，即基线长度。该双目视觉系统的可视范围如下：

(2)

图1 双目立体视觉测量系统精度分析模型

假定左右相机光轴Z轴的夹角为β，空间中的点在左右图像上的对应点x方向相面坐标分别为U1、U2。根据三角形相似，可得：

现将z对U1求偏导数然后代入U1可得：

(3)

由式(2)可知，对于一个特定的焦距和空间点，当β与x、z满足如下关系时，误差可以取得最小值：

β= 90°-arctan(z/x)

(4)

基线长度是表征视觉系统中左右相机之间相互位置关系的重要参数，它的变化不仅会引起系统结构的改变，而且会直接影响测量精度。由误差δ、市场范围w的表达式以及z与x的关系可知，z越大测量误差越大，当测量精度要求比较高时，尽可能将物体放在距离相机的距离比图中z′略大的位置上。综合考虑测量精度和市场范围两方面，最佳的测量距离为z=B/(tg(α+β)+tg(β-α))处，对应的视场范围为：w=B-2Btg(β-α)/(tg(α+β)+tg(β-α))可知，对于一个特定镜头和空间点，相机的视角α已知。z一定时，基线长度B越大，相机主光轴与Z轴间的夹角β越大，测量范围减小；B一定时，β越大，z越小，w越大，误差越小；β一定时，B越大，z越大，w越大，误差越大。

2 基于射线法的双目模型

图2所示为基于射线法的简单双目模型[15]，假定空间任意点P的世界坐标为：(Xw,Yw,Zw)，点P在两个相机的成像平面上的像点分别为P1与P2，P1和P2的像素坐标分别为：(u1,v1)和(u2,v2)，左、右相机的投影矩阵分别为：

图2 基于射线法的简单双目模型

(5)

(6)

设左相坐标系与世界坐标系重合，则此时：

(7)

(8)

由此得：

(9)

(10)

通过推导，可得矩阵形式表示如下：

Kq=l

(11)

(12)

(13)

(14)

为方便计算先求KTK,进而求得：

q=(KTK)-1KTl

(15)

上述讨论表明：只要知道两个相机的内参矩阵和两个相机间的旋转、平移矩阵，便可求出空间点的三维坐标。

3 特征点提取和匹配

本文使用的方法是通过基于边缘检测的斑点检测算法来检测投影的白色方格。本算法的主要原理是提取出图像中比周围其他像素点灰度值大的区域。本文所用的提取图像中白色方格中心点算法的具体方法如下：

首先根据一系列的由白色方格与周边区域灰度变化情况确定的连续的阈值，把输入的灰度图像转换为由多个二值图像组成的集合，阈值范围为[T1，T2]，步长为t，初始值T1取的是白色方格最外边缘最接近黑色区域部分的灰度，最终值T2取的是白色方格内部最靠近纯白色部分的灰度，则所有阈值为：T1，T1+t，T1+2t，T1+3t，……，T2。

第二步是利用灰度变换关系对每一幅二值图像中白色方格的边缘部分进行检测。只要发现某一个像素点周围以2个像素为半径的圆形区域内多个点的上下左右四个像素点之间出现明显的灰度变化，则认为此点为边界上的点。

最后就是获得灰度图像中白色方格中心的准确图像平面像素坐标信息。位置的计算方法是，对所有二值图像中检测到的白色方格边界点坐标用灰度重心法计算得到的中心坐标计算加权算数平均值，计算中用到的权值是对每个阈值下拍到的图片进行二值化处理时用到的阈值。

在第二步中，并不是所有被检测到的连通区域都可以被认为是白色方格的中心点，可以使用一些限定条件来剔除不准确的特征点。这些限定条件包括面积，形状和颜色，所需检测区域的形状又可以用方形度，或者凸度等等信息。

对于二值图像来说，需要检测的区域只可能有两种颜色——白色或黑色，本文只需要规定好需要检测区域的颜色，通过确定待检测区域的灰度值的大小就可以区分出白色方格所在区域与周边区域。

对于检测白色方格中心坐标来说，方形的连通区域是最理想的。任意形状的方形度C定义为：

C=16(S/p2)

(16)

其中，P与S分别表示该区域的周长和面积，当C为1时，代表检测到的区域的形状是一个标准的正方形，而当C的值为0时，代表该区域的形状是一个被逐渐拉长了的多边形。

另一个用来约束检测到区域的形状特征物理量是凸度。本文所使用的凸度V的定义如下式所示：

V=S/H

(17)

其中，H代表该待检区域中凸壳所占的面积。

综上所述，针对本文中设计的对投影的黑色背景下1mm×1mm的白色方格中心进行提取时，将阈值范围中起始位置设置为1，终止位置设置为150，步长设置为1，两白色方格间最小距离设置为1mm，能被检测到的白色方格最小面积设置为1mm2，最大面积设置为9mm2，能被检到的方块颜色设置为纯白色，最小凸度设置为0.9，最小惯性率的值设置为0.95。通过设计投影仪控制程序，投影白色方格，拍摄图像进行实验，实验中得到的投影的白色方格中心提取效果如图3所示，白色处表示的为提取到的白色方格。

图3 白色方格中心提取效果

进行特征点检测之后，要对检测到的特征点进行匹配。由于特征点都是间隔排列的两列白色方块的中心，所以检测到的左右相平面上的特征点都是一一对应的。利用极线约束，结合拓扑结构，先对检测到的特征点进行排序，再对特征点根据两相机间的R、T进行配对，将斑点检测算法提取到的特征点划分为多个一对一匹配对。具体方法如下：

当左相机坐标系与世界坐标系重合时，根据基于射线交汇法的双目模型，由式(9)～式(10)得：

(18)

其中，

将由Pr定义的反对称矩阵记作[Pr]×，两边同时乘以[Pr]×，由[Pr]×Pr=0得：

(19)

由于左右像机型号参数一致，标定好双目扫描测量系统后，先将提取到的左、右相机像平面特征点像素坐标按v坐标从小到大的顺序排列，由式(19)即可计算出理想情况下左相机像平面检测到的特征点对应的右相机像平面特征点的像素坐标。所有左相机像平面提取到的特征点的对应点计算完后，将对应点与检测到的右相机像平面特征点进行比对，将与计算得到的点相面距离最小的点作为拟匹配点。所有左相机像平面特征点的拟匹配点选取完毕后，如有选择同一点的，将两个相面距离作比较，较小的作为最终匹配点对。如未找到相应的点，说明未能准确提取到对应的特征点。由于之前已经按像素大小对特征点进行了排序，只需根据其他特征点的大小，按照拓扑结构，计算各相邻特征点之间的像素差，即可补全未提取到的右相机相面特征点坐标。同理，当检测到的右相机相面特征点数多于检测到的左相机像面特征点数时，也可补全未提取到的左相机像面特征点坐标。

4 玻璃坐标系的建立和坐标变换

4.1 标记点检测与匹配

实际获得的图像在形成、传输、接收和处理的过程中，不可避免地存在着外部干扰和内部干扰，因此，首先要对图像进行高斯滤波。所谓高斯滤波，实际上就是对整幅图像中各像素点的值进行加权平均的过程。这个过程中，每一个像素点的值，都由其本身和邻域内的其他像素点的值进行加权平均运算后得到。

滤波后用背景减除法对图像进行处理。具体做法是把喷涂显像剂后贴满标记点的玻璃图像减去喷涂显像剂而未贴标记点的玻璃图像。减去背景后要图像进行二值化。设定一个全局的阈值T，将大于T的像素群的设定为白色，小于T的像素群的设定为黑色。然后使用Open CV中的cv Find Contours函数对图像进行轮廓检测。图像经轮廓检测过后，标记点黑圈内外边界上的点都会被提取到。这种函数提取到的边界点精度只有像素级，为了提高边界提取的精度，还需要根据提取到的结果，对图像应用Zernike矩阵进行亚像素级别的边缘点坐标提取。所谓Zernike矩阵是指基于Zernike多项式的正交化矩阵。其所利用的正交多项式集是一种在单位圆内的完备正交集。经过以上一系列变换，最终提取到的边界点数据以链表的形式储存，可以将其转换成数组，然后利用最小二乘法拟合椭圆，其具体方法如下：

对给定的一组数据点(xi,yi) (i=1，2…，n)(至少有三个不相同的点)设与该组数据点的距离的平方和为最小的圆的方程为：

(x-xo)2+(y-yo)2=R2

(20)

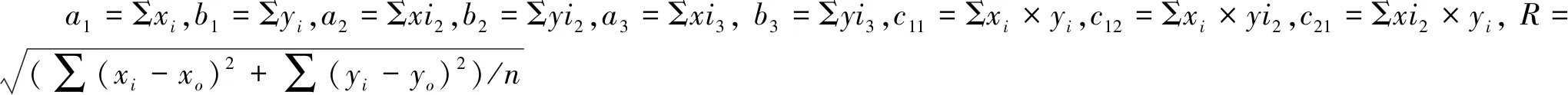
解得圆心为：

Xo= (2a1b1/n-2c11)(b3+c21-b1(a2+b2)/n-

(2b12/n-2b2)(a3+c12-a1(a2+b2)/n)/

((2a12/n-2a2) (2b12/n-2b2)-(2a1b1/n-2c11)2)

(21)

Yo= (2a1b1/n- 2c11)(a3+c21-a1(a2+b2)/n-

(2a12/n- 2a2)(b3+c21-b1(a2+b2)/n)/

((2a12/n- 2a2) (2b12/n- 2b2) - (2a1b1/n- 2c11)2)

(22)

利用最小二乘法时，参加拟合的数据的个数越多，拟合的误差就越小，拟合出来的椭圆就越接近真实的图像形状。经过最小二乘拟合后，标记点的黑圈内外边界上的点可以拟合出两个圆心，再对两个圆心进行加权平均得到最终的标记点的中心。不同边界上的点对应的权的大小即为其边界所在圆直径的大小。标记点检测效果如图4所示。

(a) 原始图像 (b) 边缘提取结果图 图4 标记点检测效果图

进行标记点检测之后，要进行标记点匹配。首先将左右相平面检测到的中心坐标按公式(20)进行匹配。这个方法可以把标记点的搜索范围从整张图像缩小到一条极线上,减小了搜索空间,但在该极线上存在多个标记点时,就需要增加其他的约束，这里引入图像绝对距离比约束。在针孔模型下，相机成像是一个线性变换，若将同名点连线，不同图像上对应线段的比值相等。在图5 中，三个同名点在两幅不同图像上，假定在左边图像上的像点命名为p1，p2，p3，在右边图像上的像点命名为q1，q2，q3；若互为同名点，则其图像绝对距离之比相等： |p1p2|/|p1p3|=|q1q2|/|q1q3|，考虑到相机畸变的影响，|p1p2|/|p1p3|≈|q1q2|/|q1q3|。

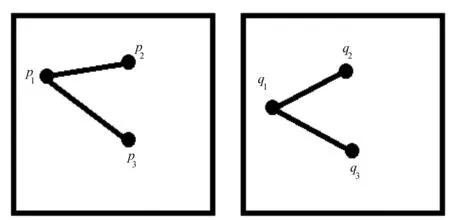
图5 图像绝对距离比约束示意图

在移动测量系统的过程中也需要进行标记点的匹配。这里的匹配是确定新测量的传感器坐标系中的标记点有哪些是上次测量时已经转换到工件坐标系中的点，哪些是新出现的点。由于单个标记点没有特征，但是每个标记点间的距离是确定的，计算每个标记点和其周围标记点之间的距离，只要移动前后某两个标记点与周围各点间的距离有一半以上是匹配的，则可以认为两个点是同一个点。

4.2 玻璃坐标系的建立和变换矩阵的求解

在初始位置测得标记点在相机坐标系下的坐标后，任取三点建立玻璃坐标系。如图6所示，设所取三点分别为A(x1,y1,z1)，B(x2,y2,z2)，C(x3,y3,z3)，A点为坐标系原点O，向量AB为X轴C在oxy平面内，则ox=(l1,l2,l3)=(x2-x1,y2-y1,z2-z1)，AC= (x3-x1,y3-y1,z3-z1)，解得：

oz=(r1,r2,r3)=ox×AC

(23)

oy=(m1,m2,m3)=ox×oz

(24)

图6 在初始位置建立的特定玻璃坐标系

设相机坐标系与玻璃坐标系之间的变换关系为：

(25)

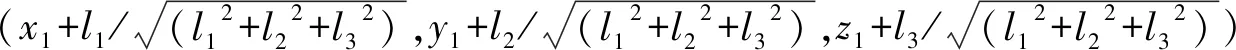
(26)

记为：

(27)

解得：

(28)

之后向玻璃上投影白色方块，将测得的方块中心点在相机坐标系下的坐标代入式(28)便可求得其在工件坐标系下的坐标。完成在初始位置对玻璃的测量后，移动测量系统继续对玻璃其他部位进行测量。如图7所示，获得三个公共点在相机坐标系下的坐标为：D(x4,y4,z4)，E(x5,y5,z5)，F(x6,y6,z6)；相应的在建好的玻璃坐标系下的坐标为：G(x7,y7,z7)，H(x8,y8,z8)，I(x9,y9,z9)。按前述方法建立坐标原点在D(G)点的新玻璃坐标系，设求得的基于相机坐标系下坐标建立的坐标系X轴的方向向量为(l4,l5,l6)，Y轴的方向向量为(m4,m5,m6)，Z轴的方向向量为(r4,r5,r6)，基于原玻璃坐标系下坐标建立的新玻璃坐标系X轴的方向向量为(l7,l8,l9)，Y轴的方向向量为(m7,m8,m9)，Z轴的方向向量为(r7,r8,r9)。按前述的方法解得相机坐标系与新建玻璃坐标系之间的变换关系为：

(29)

图7 移动本文设计的测量系统后坐标变换

原玻璃坐标系与新建玻璃坐标系之间的变换关系为：

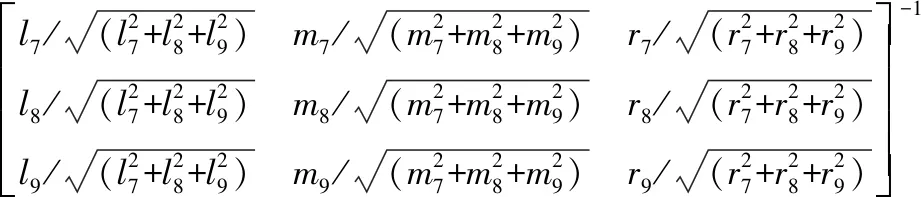
(30)

解得原玻璃坐标系与相机坐标系之间的变换关系为：

(31)

由此便可算出移动测量系统后测得白色方块中心在初始位置时建立的玻璃坐标系下的坐标。通过多次移动测量系统，最终可以实现整块玻璃的测量。

5 实验结果

实验中首先对双目测量系统进行了标定，用投影仪向标定板投射白光，通过改变标定板摆放位置然后分别用左右相机同时对标定板进行拍摄得到一组图像。获得了12组图像来进行标定，标定得到重投影误差为1.36μm，双目系统标定所得内外参如下：

左、右像机内参为：

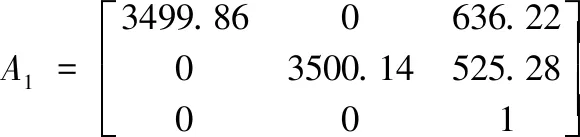
左右像机畸变为：

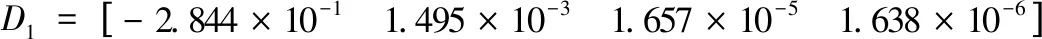
两像机间的外参为：

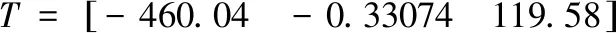
标定得到双目扫描测量系统内外参数后，在不移动系统的情况下，对挡风玻璃表面三维形貌进行测量。如图8所示，均匀喷涂薄薄的一层显像剂后，向挡风玻璃表面投影黑色背景下的大小为1mm×1mm的两列间隔排列的白色方格图像。按照前文介绍的方法，对左右像机拍摄的图像进行特征提取和匹配。将得到的挡风玻璃上的上的多组匹配点对代入前文介绍的基于射线法的双目模型中，从而得到这些点的三维坐标，建立玻璃坐标系，将测得的相机坐标系下的坐标转化为玻璃坐标系下的坐标。多次投影后逐渐让棋盘格图像布满整个视场范围内的全部玻璃平面，实现对视场内玻璃表面的测量。移动测量系统通过投影和坐标系变化，获得移动系统过后视场内玻璃表面在之前建好的玻璃坐标系下的坐标。多次移动测量系统，实现对挡风玻璃的精确测量。分别对测得的高精度平面点三维坐标和挡风玻璃表面点三维坐标用尽量高阶次的方程进行平面和曲面拟合，并分别计算出平面度误差和曲面拟合的RMS误差。最终将获得的三维坐标平面拟合效果如图9所示。挡风玻璃测量实验中的特征点提取和匹配效果如图10所示，最终得到的视场内玻璃上所有特征点曲面拟合效果如图11所示，测得的标记点在玻璃坐标系下的坐标曲面拟合效果如图12所示，最终测得的整块玻璃的曲面拟合效果如图13所示。

图8 测量挡风玻璃实验图

图9 高精度平面投影测量实验中测得点平面拟合效果

图10 特征点提取和匹配效果

图11 视场内测得点曲面拟合效果图

图12 标记点曲面拟合效果图

图13 整个挡风玻璃测得点曲面拟合效果图

6 结论

(1)视场内测得点曲面拟合效果图可知，在摄像机标定、特征提取和匹配后，根据基于射线法的双目模型算法，对挡风玻璃上相邻两块投影斑块间的距离进行测量，双目标定重投影误差为1.36μm，挡风玻璃整体测量RMS误差小于±1mm，能满足挡风玻璃测量RMS误差不超过±2mm的国家标准，可见该测量系统基本能满足挡风玻璃测量的要求。

(2)通过对比单视场内高精度平面扫描测量误差和整个挡风玻璃测量误差可知，多次投影扫描的数据融合和拼接本身引入了测量误差，误差小于0.5mm，可以通过扩大单次投影测量范围，减少测量次数以减少误差。

(3)通过建立玻璃坐标系较好的实现了视场范围有限的情况下对大尺寸挡风玻璃表面的测量，建立的变换模型本身没有误差，只要标记点提取精度足够高，就可以得到足够好的坐标变换精度。