偏心轴磨削迭代学习模糊自适应PID控制技术研究*
2019-04-08裴召俭韩秋实彭宝营李启光
裴召俭,韩秋实,彭宝营,李启光
(北京信息科技大学 机电工程学院,北京 100192)
0 引言
偏心轴是工业机器人RV减速器、空调压缩机等设备的核心零件,要求有较高的轮廓加工精度,目前加工高精度偏心轴的磨床主要是日美等发达国家生产,因此研究提高偏心轴加工精度的技术与设备具有十分重要的意义。
目前对偏心轴轮廓磨削加工技术的研究主要有偏心轴加工数学模型的研究,偏心轴加工控制方法的研究等。如范晋伟等[1]学者提出了偏心轴随动磨削数学模型,利用切点跟踪的方法推出了偏心轴的运动轨迹方程。李启光等[2]提出了基于平面刚体运动的偏心轴磨削X-C联动关系模型。在加工过程控制方面,PID控制本身具有较好的鲁棒性,但是在实际生产加工过程中对于一些复杂的工作情况,如提高非圆轮廓精度,普通的PID是无法解决的,彭宝营等提出了X-C直驱平台非线性耦合控制方法[3]。非常规PID控制应用于偏心轴磨床还需进一步研究。本文通过研究偏心轴在偏心轴数控磨床X-C轴联动加工控制下,采用迭代学习模糊自适应PID控制器,PID参数可以实时调整,该系统具有良好的自适应能力和鲁棒性,能够快速有效收敛继而减小偏心轴廓形误差[4]。最后利用MATLAB仿真软件,对偏心轴高速磨削进行仿真,为偏心轴加工精度的提高提供理论依据。
1 偏心轴轮廓加工数学模型
偏心轴在加工过程中是由X轴往复运动,C轴绕偏心轴主轴颈O1进行工件旋转,P点为偏心轴磨削点,在磨削过程中为了保证偏心轴的轮廓成形,偏心轴要始终与砂轮始终相切,本文采用恒磨除率加工方式进行加工,图1为偏心轴随动磨削示意图。

图1 偏心轴数控磨削数学模型
由几何关系可知偏心轴磨削点轨迹方程为:

(1)

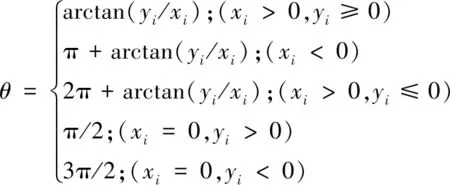
(2)
(3)
砂轮中心的运动方程为:
(4)
本文讨论的偏心轴偏心距e=3.926mm,偏心轴摆轴颈半径r=20.64mm砂轮半径R1=250mm。根据以上公式可以得到偏心轴磨削点的移动轨迹如图2和砂轮位移曲线如图3所示。

图2 偏心轴磨削点位置轨迹图

图3 砂轮位移与偏心轴主轴颈转角的关系
由以上可知偏心轴磨削为非圆类轮廓磨削,从图3可以看出砂轮架的位移是时刻都在变化的,因此偏心轴在加工过程中会产生磨削力的变化,从而导致工件加工质量的降低,会产生廓形误差及表面粗糙度,波纹等。
2 偏心轴廓形误差分析
2.1 偏心轴X-C联动加工原理
偏心轴加工过程中由偏心轴磨床X轴带动砂轮往复运动和C轴带动工件旋转组成形成X-C联动完成偏心轴加工,图4为偏心轴磨削X-C轴联动加工原理图。其中式(5)为偏心轴X-C联动加工公式[6]:
(5)

图4 偏心轴磨削X-C轴联动加工原理
2.2 偏心轴X-C轴跟踪廓形误差
偏心轴磨削过程中的X-C轴跟踪误差主要是偏心轴磨床系统的伺服误差,就是在同一时刻X-C轴同时发出加工位置指令与实际加工位置之间的误差[7],控制偏心轴的跟踪误差是有效减小偏心轴的廓形误差的主要方式。
X轴跟踪误差如图5所示,εx为偏心轴在X方向的跟踪误差造成的廓形误差根据几何关系即可求得:
(6)
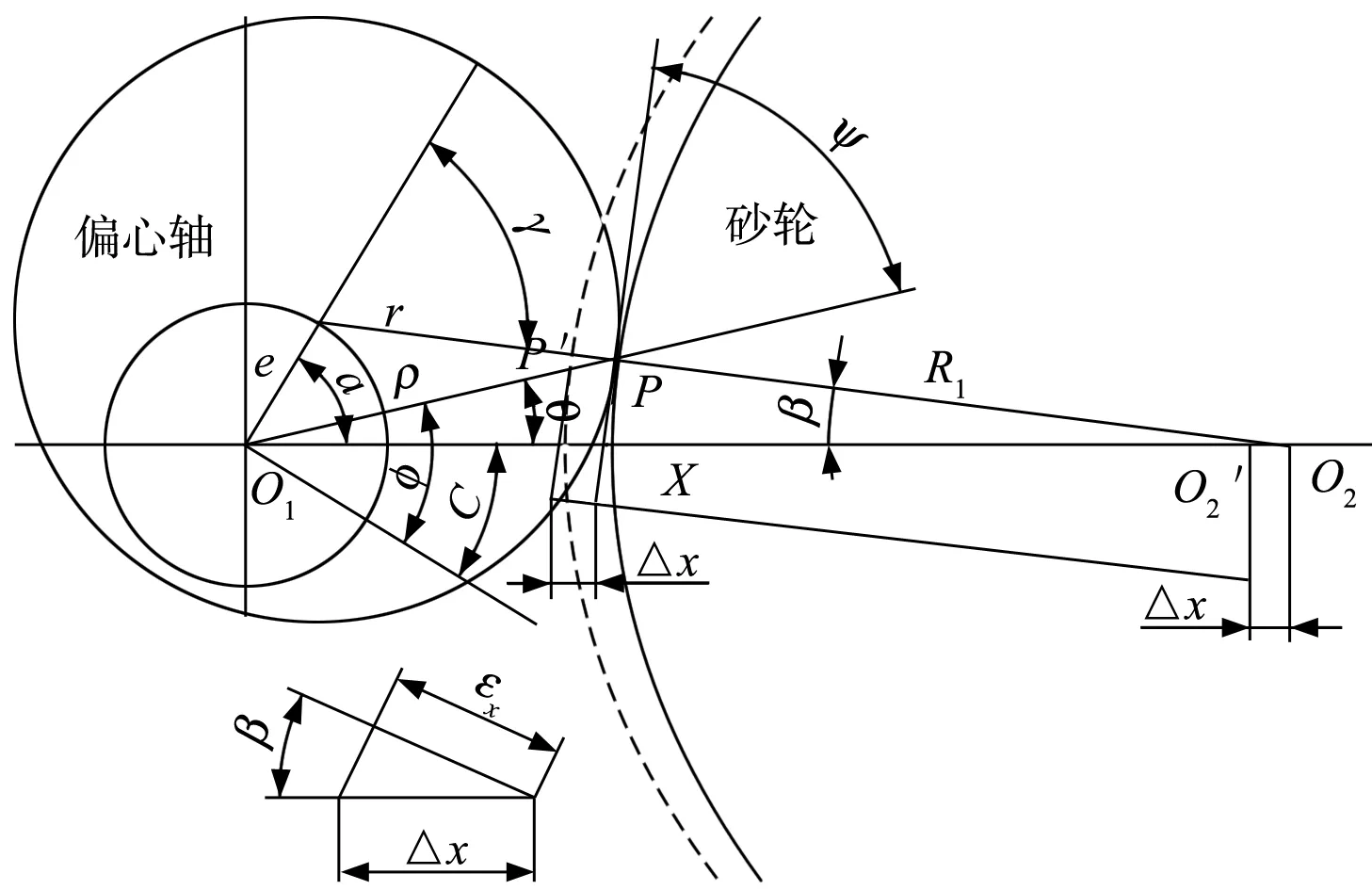
图5 偏心轴X轴跟踪误差
由于偏心轴磨削为非圆磨削,所以偏心轴在磨削时由于X-C在联动时必须保持同步,因此C轴的滞后或者超前都会引起廓形误差[8],如图6为偏心轴C轴跟踪误差图。

(7)
通过式(6)和式(7)计算,就可得到偏心轴廓形误差计算公式:
(8)
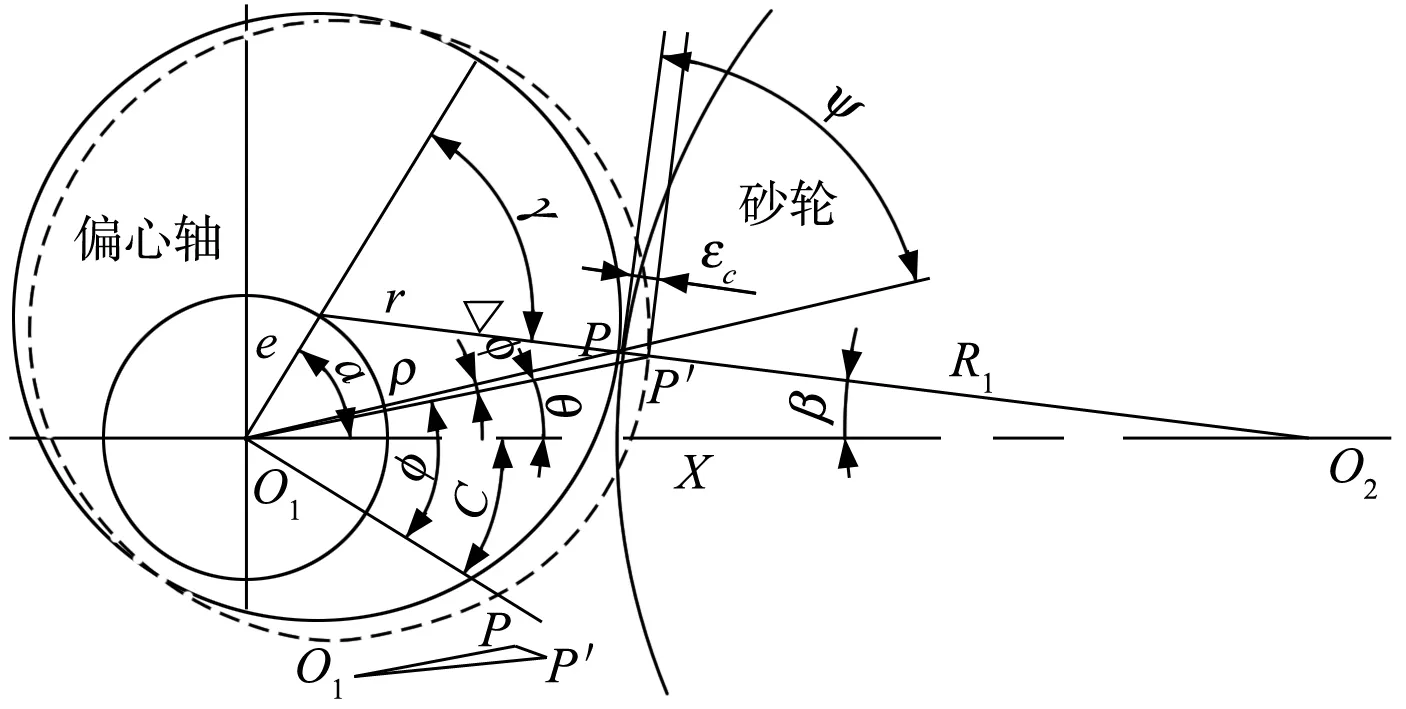
图6 偏心轴C轴跟踪误差
3 偏心轴磨削模糊自适应PID迭代学习控制器设计
3.1 偏心轴磨削模糊自适应PID迭代学习控制系统基本结构
模糊自适应PID迭代学习控制算法是基于普通PID的基础上,通过模糊规则对PID三个参数进行实时调整,提高偏心轴廓形误差的收敛速度及减小偏心轴的廓形误差,最终实现对偏心轴加工的期望值的完全跟踪,图7为偏心轴模糊自适应PID迭代学习控制器结构图。

图7 偏心轴模糊自适应PID迭代学习控制器结构图
3.2 建立PID模糊控制器模型
偏心轴模糊自适应迭代学习控制器输入的是系统输出的X-C轴的跟踪误差和误差变化率,而模糊控制器的输出是PID的变化量,PID的变化量再与普通PID相加实现PID的整定,在PID参数中Kp为偏差的比例系数、Ki为积分系数、Kd为微分系数。现定义偏心轴加工误差E,误差变化率Ec和Kp、Ki、Kd的模糊集为{负大,负中,负小,零,正小,正中,正大}即{NB,NM,NS,ZO,PS,PM,PB},创建模糊规则表如表1所示,利用MATLAB中的Fuzzy工具箱建立变量隶属度函数[10]如图8所示。

表1 Kp、Ki、Kd模糊推理规则表

图8 变量隶属度函数
表1中的E、EC、Kp、Ki、Kd遵循的模糊规则是“IFEis…andECis…then PID is…”,其中第一条规则如下:
IFEis NB andECisNBthenKpisPB;
IFEisNBandECisNBthenKiisNB;
IFEisNBandECisNBthenKdisPS。
3.3 X-C轴模糊PID控制器设计
如图9所示,模糊自适应PID迭代学习控制器是基于普通PID的基础上设计的,它是根据偏心轴在加工过程中的误差和误差的变化率作为输入信号,通过模糊自适应控制器,分别求出PID三个参数的补偿量,再与经验PID的参数Kp0、Ki0、Kd0相加,求出最佳的PID参数,从而提高偏心轴的加工精度,其中偏心轴磨床X-C轴经验PID的参数如表2所示。而迭代学习控制器是将模糊自适应PID控制器进行迭代,再选出最好的模糊自适应参数从而达到模糊自适应最好的控制效果,通过模糊自适应迭代学习控制器分别对偏心轴磨床X-C轴进行控制从而减小偏心轴廓形误差,提高偏心轴的加工精度。

表2 偏心轴磨床X-C轴经验PID参数

图9 模糊自适应PID迭代学习控制器仿真程序图
4 仿真实验及验证
4.1 偏心轴磨削廓形误差控制仿真模型
为了对偏心轴X-C联动磨削廓形误差进行仿真,首先通过偏心轴数学模型得出偏心轴X-C轴的理论期望值,由式(3)可以求得出偏心轴的理论极径夹角以及极径值,由式(4)可以得出X轴砂轮的运动中心轨迹。应用PMAC Servo Analyzer软件求得偏心轴磨床的X-C轴的传递函数[11],建立偏心轴X-C轴联动模糊自适应PID迭代学习仿真程序模型如图10所示,通过若干次的迭代学习得出理想的廓形误差。
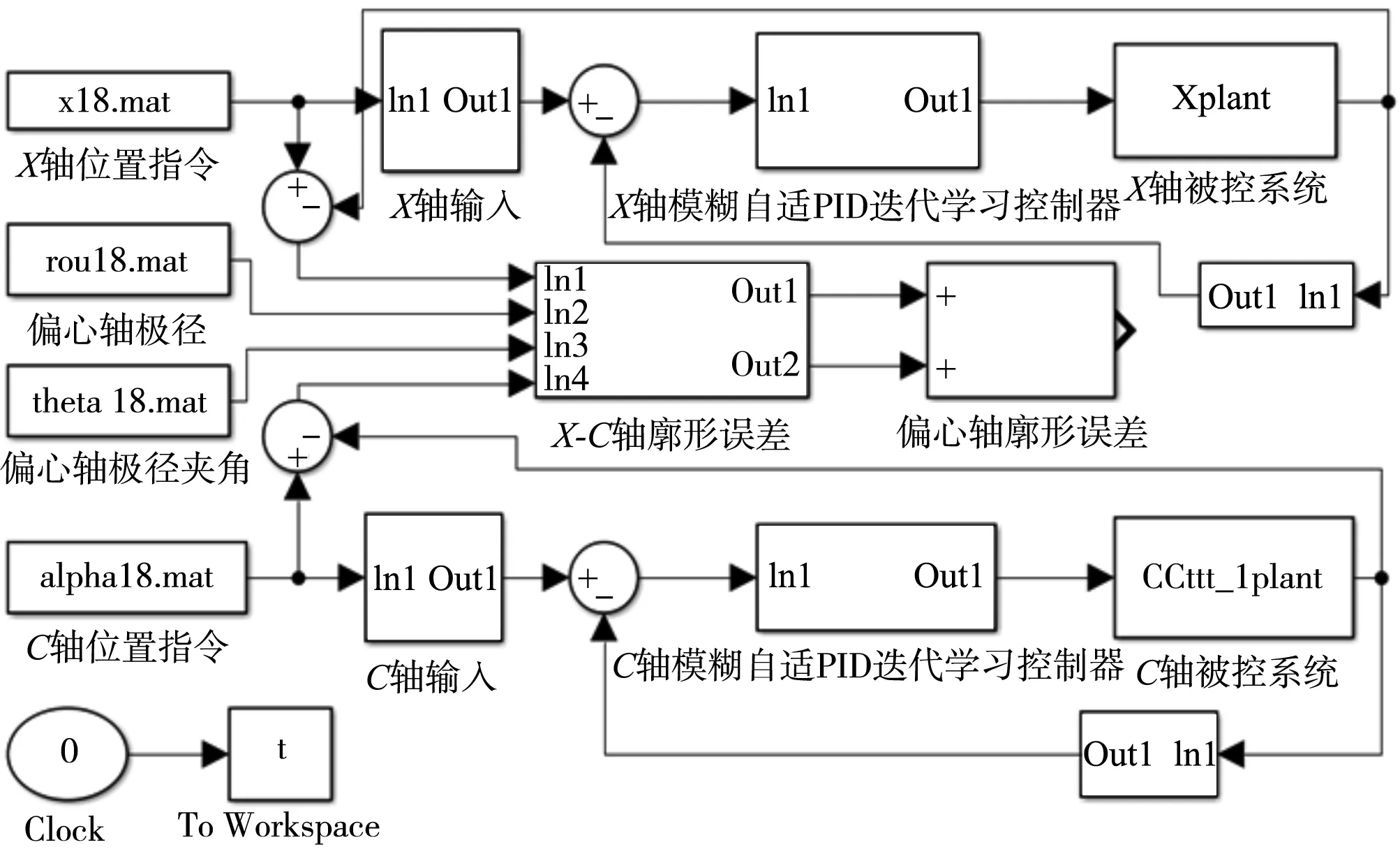
图10 偏心轴廓形误差模型simulink仿真程序图
4.2 偏心轴磨削X轴跟踪误差
首先对偏心轴磨削对X轴单独进行模糊自适应PID迭代学习控制,选择偏心轴工件在高速旋转的条件下进行仿真,高转速为34r/min,旋转一周的时间为1.8s,工件旋转一周时PID参数的变化曲线如图11所示,X轴跟踪误差如图12所示。

图11 34 r/min时X轴PID参数变化
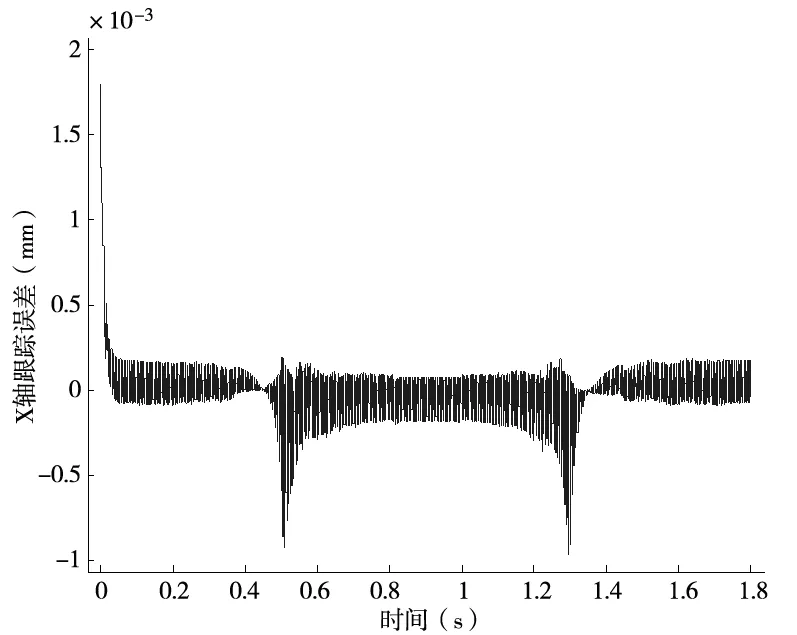
图12 34 r/min时X轴跟踪误差
通过分析图11可知X轴在加工过程中PID参数表在时刻变化,说明模糊自适应迭代学习控制器能够实时调整PID参数,通过图12可以看出X轴的最大跟踪误差1.5μm因此说明了模糊自适应迭代学习控制器能够有效减小X轴的跟踪误差。
4.3 偏心轴磨削C轴磨削跟踪误差
偏心轴磨削对C轴进行模糊自适应PID迭代学习控制,选择工件转速为34r/min旋转一周的时间为1.8s,工件旋转一周PID变化曲线如图13所示,C轴跟踪误差如图14所示。

图13 34 r/min 时C轴PID参数变化
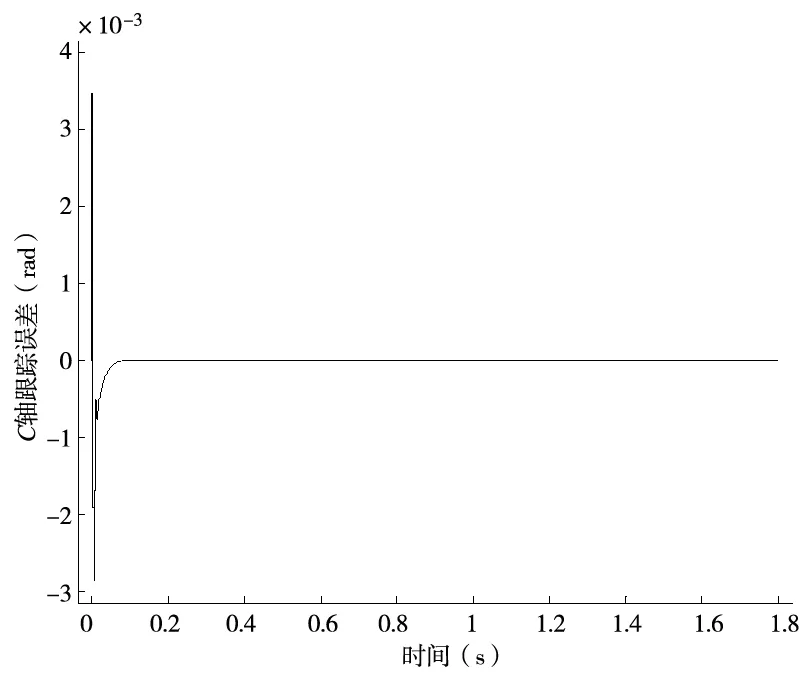
图14 34r/min时 C轴跟踪误差
通过分析图13和图14可以看出C轴在模糊自适应迭代学习控制下跟踪误差在开始时比较大,同时PID参数也在调整,等误差稳定以后PID参数趋于稳定,C轴跟踪误差最大值为3.5μm,说明模糊自适应迭代学习控制器有效的控制了C轴的跟踪误差。
4.4 偏心轴廓形误差
当偏心轴转速在34r/min时,分别利用模糊自适应迭代学习控制器和普通PID控制器进行仿真,图15为模糊自适应迭代学习控制得到的偏心轴廓形误差,比较两种控制器得到的廓形误差如图16所示。

图15 模糊自适应PID迭代控制偏心轴廓形误差

图16 普通PID与模糊自适应PID廓形误差比较
为了防止仿真结果的偶然性,同理可以得出当偏心轴C轴转速为17r/min时的仿真实验结果,通过分析模拟仿真结果可以看出差模糊自适应PID迭代学习控制器和普通PID控制器下的偏心轴廓形误差性能如表3所示。

表3 偏心轴廓形误差比较
4.5 仿真结果分析
从偏心轴廓形跟踪仿真结果来看,偏心轴模糊自适应PID迭代学习仿真过程中X、C轴的PID三个参数是在变化的,这就说明了该控制器实现了变参数在线补偿的功能,采用模糊PID控制器,PID参数可以实时变化,系统具有良好的自适应能力和鲁棒性。通过此次仿真验证了模糊自适应PID迭代学习控制器能够实时调整PID参数,有效快速收敛,减小偏心轴在高速状态的廓形误差。
5 结论
本文将模糊自适应PID迭代学习控制引入偏心轴X-C联动磨削加工中,在偏心轴加工数学模型的基础上进行X-C轴偏心轴高速磨削控制,经过仿真实验证明模糊自适应PID迭代学习控制能够快速收敛跟踪,与普通PID相比得到的偏心轴廓形误差明显减小,较明显的提高了偏心轴磨削的加工精度,表明了迭代学习模糊自适应PID控制方法更适合偏心轴磨削,能有效提高偏心轴的加工精度,为以后开发偏心轴磨床提供了更好的控制方法和理论基础。
