基于四元数互补滤波的小型四旋翼姿态解算*

李二闯，张建杰，袁 亮，吴金强

(新疆大学 机械工程学院，乌鲁木齐 830000)

0 引言

由于小型、低成本的无人机特别适合各种应用，在研究的过程中，无人机的姿态解算又是研究无人机的一个关键性的问题[1]。在小型四旋翼无人机的飞行控制研究过程中，姿态解算的精度和速度又是姿态解算的主要核心研究内容之一，姿态解算的精度和速度是评估小型四旋翼无人机飞行控制算法的关键性指标。过去由于传感器体积和精度的限制，不适合使用到小型四旋翼无人机的姿态解算上，但是随着科技的发展，特别是微电子方面的发展，促进了小型四旋翼无人机在姿态解算方面的一次进步，使得小型四旋翼无人机姿态解算的硬件的要求上有了很大的选择性，常采用捷联惯性测量单元(INERTIAL MEASUREMENT UNIT,IMU)。在一定程度上极大地促进了小型四旋翼无人机在姿态解算的发展。小型四旋翼无人机的姿态角可以使用微机械陀螺仪进行测量，通过姿态角测量实现对无人机姿态的控制。单独使用微机械陀螺仪进行小型四旋翼的姿态的解算又存在较大的误差，所以解决小型四旋翼无人机的姿态解算的有效途径是利用微机械陀螺仪和其他的传感器组件进行结合使用，利用多传感器的组合实现小型四旋翼无人机姿态解算中多姿态数据的融合得出准确有效的姿态角[2]。

在姿态解算中，卡尔曼滤波器的使用最为广泛，利用动力学系统和信号噪声的提前了解的这些特性，但是其复杂的逆矩阵计算在小型四旋翼无人机的控制系统中使用非常困难的[3]。应用非常广泛的扩展卡尔曼滤波器算法(EKF)是一种高精度姿态解算算法，然而 EKF 存在一些缺陷，计算量比较大、在线性化假设不成立的情况下滤波器是不稳定的[4]。利用粒子滤波能够解决扩展卡尔曼滤波所带来的缺陷，但是利用粒子滤波算法的计算量太大[5-6]。

本文设计的互补滤波器是基于四元数的形式的。在惯性测量仪器的精度较低的情况下，使用互补滤波算法可以有效地改善测量仪器精度差的状况。四元数的使用可以有效的降低计算的复杂度和难度并减少计算量，同时其旋转特性可以解决小型四旋翼无人机姿态解算中存在的奇异性问题。在小型四旋翼无人机运动加速度时，引入计算加速度计信任度的方法。最后给出具体实现步骤并在自主搭建的实验平台上进行了实验的验证和误差的分析。实验结果表明该互补滤波方法能够准确快速的解算出无人机的姿态。

1 姿态解算的原理

载体坐标系相对地理坐标系的姿态矩阵的求解从而求解姿态角度，这是四旋翼无人机姿态解算的方法途径。

1.1 定义坐标系

1.1.1 参考坐标系

OXiYiZi是参考坐标系是运动载体在地球表面进行惯性导航解算所使用的坐标系。XjYj是在同一个环境下的同一个水平面内，两者分别指向的方向是指北和指西，Zi是垂直于无人机指向天。并且这个坐标系中的三轴满足右手定则。

1.1.2 载体坐标系

载体坐标系OXjYjZj是测量传感器所在的位置的坐标系。载体坐标系中绕Zj轴转动的角度被称作航向角用符号ψ表示，绕Xj和Yj轴旋转形成的角度分别称作横滚角、俯仰角。他们的字母表示分别是θ和β角。

1.2 四元数姿态表示方法

四元数姿态表达式原理来自两个坐标系之间的坐标的转换是具有4个参数的姿态表达式。四元数用符号h表示，它的4个参数都是矢量[2]。

(1)

式中，Rx、Ry、Rz代表在参考坐标系中的矢量分量的位置表示，θ是矢量在动坐标系上的转动的角度值。

由动坐标到参考坐标的姿态矩阵表达式：

(2)

使用四元数来表达欧拉角：

(3)

θ=-arcsin(2(h1h3-h0h2))

(4)

(5)

四元数与欧拉角之间的表达式：

(6)

(7)

(8)

(9)

(10)

实验中所使用到的四元数都是经过处理的四元数，即都是规范化处理的四元数，并且在每次滤波结束后都重复这样的操作。

1.3 姿态导出

1.3.1 三轴陀螺仪导出姿态：

由文献[7]可知，先定义四元数的运动学微分方程为：

(11)

Ωg=Ω+b+η

(12)

1.3.2 加速度信任的计算

引入加速度计信任度的计算主要是防止无人机在飞行的过程中受到外部加速度的干扰，从而来提高加速度的精度，计算如下：

(13)

式中，a为加速度的实际测量值，u是根据手册查找的加速度计分辨率。

(14)

(15)

上边公式中的参数都是根据真实的实验得出的结果值，a为加速度的实际测量值，F表示加速度信任度，可以看出其中b值越小，则加速度计信任度越高。

1.3.3 由三轴加速度计/三轴磁力计导出姿态

加速度计的输出模型为[8]：

(16)

式中，V·、gn、μ分别为载体运动速度，在重力场下的导航坐标的轴分量和加速度计的实际的一些白噪声和测量噪声。

磁力计的输出模型可表示为：

(17)

式中，mn和mb分别为在导航坐标系下和机体坐标系的地磁场的三轴分量，η为磁力计的量测噪声。

载体的姿态矩阵求解使用的是FAQ[9]法。但是，三轴加速度计和三轴磁力计解算出的姿态对振动等噪声的敏感较强并且动态响应较差。所以，为了高质量的姿态信息，需要融合陀螺仪信息来提高姿态输出信息的准确性。

1.4 四元数互补滤波器

1.4.1 四元数互补滤波器

由于加速度计低频特性比较好，因为加速度的角度可以直接算出来，没有累积误差，所以长时间后也比较准。而陀螺仪长时间后由于积分误差的累加，会造成输出误差比较大，甚至无法使用。所以用互补滤波法根据他们的特性取长补短进行姿态解算，每过一段时间就让加速度计去校准一下陀螺仪。互补滤波就是在短时间内采用陀螺仪得到的角度作为最优值，定时对加速度采样来的加速度值进行取平均值来校正陀螺仪的得到的角度。短时间内用陀螺仪比较准确，以它为主；长时间用加速度计比较准确，这时候加大它的比重，互补滤波——加速度计滤掉高频信号，陀螺仪滤掉低频信号，互补滤波器就是根据传感器特性不同，通过不同的滤波器，然后再相加得到整个频带的信号。互补滤波器可以有效融合三轴加速度计、三轴磁力计信息和三轴陀螺仪信息，可以看作是一个一阶微分系统。结合三轴加速度计、见图1。三轴磁力计并且使用FAQ算法可以解算出一组可以参考的四元数。

图1 四元数互补滤波

设四元数误差量:

(18)

H是四元数规范化处理后的值。

四元数下的互补滤波算法式如下：

(19)

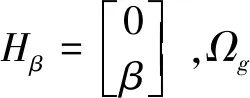
2 实验和结果

2.1 系统组成

主要使用三轴加速度计、三轴陀螺仪和三轴磁强计组成了本文的无人机姿态解算控制系统。主控芯片主要进行数据的融合和接收遥控器发射的控制信号进行运算并输出PWM信号。系统组成如图2所示。

图2 无人机系统结构图

2.2 算法流程实验验证

根据互补滤波的算法原理，算法执行流程如下：

(1)设置误差四元数的初值和陀螺仪漂移估计初值

(2)依赖于三轴加速度计和三轴磁力计并且结合使用FAQ算法可以解算出一组可以参考的四元数。

为了验证本文的算法，采用主芯片是STM32F103ZET6的STM32开发板进行试验测试，本实验开发板集成了MPU6050、磁强计HMC5883的姿态测量系统。除此之外，本实验利用开发板的串口把采集到的数据上传至上位机进行数据的分析。

本实验采用模拟的无人机实验平台，这一平台可以模拟出多种情况的运动效果。本次的实验采用的是30Hz的采集频率，并且采集次数大于600次，实验对比见图3。

图3 实验对比(*标注的为加入本文算法的显示)

使用本文算法和没有使用本文算法的对比图可以看出，使用本文算法以后的运动情况比这之前有着明显的改善，在无人机的姿态解算方面精度的提高是效果显著的。静止、匀速、加速状态下本文所设计的基于四元数的互补滤波器都能很好地跟踪测量姿态，并有效地降低姿态测量的误差，使姿态测量误差保持在±0.1°。(特别说明，本实验以俯仰状态即Y轴作为测量值。另加速度为X轴加速度值。图像为放大100后的结果。)

3 结论

本文研究的是在本文所设计的基于四元数互补滤波的基础上，根据多传感器进行数据融合，在不同状况下采取数值并且引入加速度计信任度，实现了无人机姿态解算上的测量误差有效降低。根据以上的实验数据和分析可以得出，基于四元数的互补滤波算法能够比很好的解算出小型四旋翼无人机的姿态。和传统的姿态解算算法相比，本文中所设计的方法仅需少量的计算就可以完成一个周期的解算，有效的降低了无人机在姿态解算中的计算量，并且在无人机姿态解算的准确度上得到了有效的提升，并有效地降低姿态测量的误差，使姿态测量误差保持在±0.1°，比较适合小型的低成本的四旋翼无人机的姿态解算使用。