高精度随动数控凸轮轴磨床模态分析*

张 氢，陈文韬，陈 淼，王玉琢，郑大腾

(1.同济大学 机械与能源工程学院，上海 201804；2.江西杰克机床有限公司，江西 吉安 343008；3. 井冈山大学机电工程学院，江西 吉安 343009)

0 引言

高效高精度磨削是最终获得高精密零件的非常重要的技术手段，也是先进制造技术的重要组成部分。产品不断向高速、精密发展为零件的现代机械高精度加工提出了新的挑战[1]。国内很多学者都对各种类型机床的动态特性进行了研究。马跃等[2]通过模态试验获得机床的动态性能，并以此为依据提出改进建议；李伟等[3]通过对五轴联动精密微铣削机床进行模态试验找到结构的薄弱环节，并找出了应规避的主轴转速。李康举等[4]利用有限元和模态试验相结合研究了加工中心的不稳定模态。目前多大数研究是以车床和加工中心为主，对于磨床的模态试验分析方面的研究较少。特别是对于具有不同砂轮、更多自由度的高速随动磨床，其本身结构大、运行速度高、连接复杂，本文将对新型JKMG8330G高精度随动数控凸轮轴磨床进行模态试验，探究该磨床的动态特性和结构的薄弱点。

1 模态试验理论

实验模态分析可分为传统实验模态分析和环境激励实验模态分析两种。传统的实验模态分析利用频响函数FRF或者脉冲响应函数 IRF 进行估计，它必须通过激振器或力锤施加激励，并同时测量系统响应，计算传递函数矩阵，从而得到模态参数。但此次测试的磨床体积庞大，质量达到20t，且布局比较密集，难以利用激振器产生的脉冲冲击或者正弦波激励激发磨床的模态。经过反复试验，确定本次测试主要利用环境激励法。直接采用环境激励的方式，在激励未知的情况下利用结构的响应点输出的自功率谱以及与参考点输出之间的互功率谱幅值、相位、相干函数、传递率等来识别系统的模态参数[5]。环境激励的模态分析原理如下：

将磨床视为一个多自由度的线性定常系统，则其运动微分方程可表示为：

(1)

式中，[M]、[C]、[K]分别称为质量矩阵、阻尼矩阵和刚度矩阵，均为实对称矩阵。{x}是各测点的响应，可以是位移、速度或加速度。{f(t)}是作用在各测点上的激励力。

对式(1)进行傅里叶变换可得：

(-ω2[M]+jω[C]+[K]){X(ω)}={F(ω)}

或

{X(ω) }=[H(ω)]{F(ω) }

(2)

其中，[H(ω) ]=(-ω2[M]+jω[C]+[K])-1为传递函数矩阵。

对磨床的k点施加激励并在a点测量响应就可得到传递函数矩阵中第a行k列的元素：

(3)

式中，fk为点k处的激励，xa为点a处的稳态响应，n为识别模态的总阶数，{φ}ar为第r阶模态的振型在a点处的振型向量，{φ}kr为第r阶模态的振型在点k处的振型向量，Mr、Cr、Kr分别为第r阶模态质量、模态阻尼和模态刚度。

1.1 自互功率谱理论

如果环境激励情况下的输入信号为白噪声，是平稳随机过程，那么其功率谱密度函数在所有的频率内是近似均匀分布的，则：

fk(ω)=f(ω)=C1

(4)

(5)

式中，C1为常数，hi(ω)为集总频响函数。

定义参考点p与其他参考点之间的响应比为传递率αa(ω)，则：

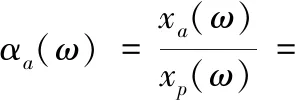
(6)

该式是在假定结构的各阶模态完全正交，忽略其他阶模态在某阶振动的贡献的基础上推导的[6]。当p为参考点时，那么会有一个确定的振型矢量{φ}pr与固有频率ωr对应，即分母是不变的，第r阶的振型可以由每个点的传递率αa(ω)得到：

αa(ω)=C2{φ}ar

(7)

式中，C2为常数。

根据经典的功率谱估计方法——周期图法的计算公式可得a点处的自功率谱Pa(ω)和p与a两点响应的互功率谱Pap(ω)分别为：

(8)

(9)

由上式可知,自功率谱Pa(ω)与传递函数的模|hi(ω)|存在平方关系，且自功率谱Pa(ω)和互功率谱Pap(ω)有相同的形式，因此三者具有相同的极点，可以利用自功率谱和互功率谱代替传递函数的幅值图进行固有频率的识别。

1.2 半功率带宽法

系统的阻尼比可以采用半功率带宽法进一步求得[7]：

(10)

2 随动磨床的模态试验

2.1 试验条件

本次试验模拟实际加工过程，实验所需的仪器见表1。用力锤在砂轮架上某一固定点以相同的力连续敲击，用PCB三向压电加速度传感器测量各测点在3个坐标轴方向上的加速度，并将信号传输到DH5902数据采集分析系统，最后用PC端的DHDAS测试系统软件对数据进行分析处理。

表1 实验主要仪器

2.2 试验建模和测点布置

JKMG8330G高精度随动数控凸轮轴磨床如图1所示，主要由砂轮架、头架、尾架、静压导轨、床身和主轴组成。根据磨床整机的结构外形建立线框图，并依据有限元划分网格的基本原理，在线框图上均匀布置62个测点，测点布置如图2所示。

图1 随动凸轮轴磨床整机

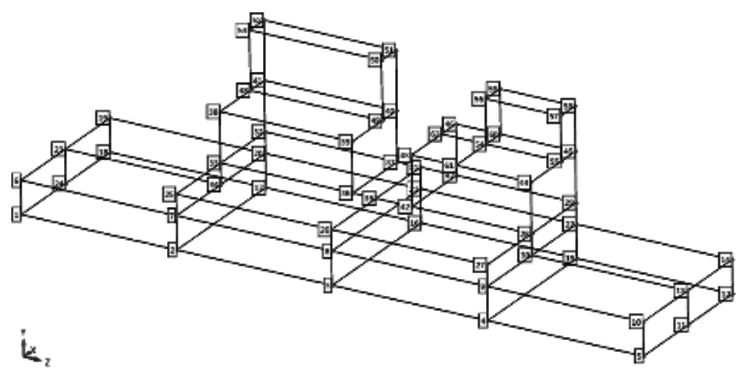
图2 随动凸轮轴磨床整机测点布置

由于整机尺寸较大，测点分布间距较大，对每个子部件往往只能由几个测点的数据来表征其振动特征，因此整机的模态测试主要是为了得到整机的整体振动模态和各部件的振动情况。在整机的模态试验之后，还需对整机试验中振动较大的部件进行局部的模态试验，下面仅以砂轮架局部模态测试为例进行说明。图3为该磨床的砂轮架，图4为根据砂轮架的外形布置的55个测点位置。

图3 随动凸轮轴磨床砂轮架

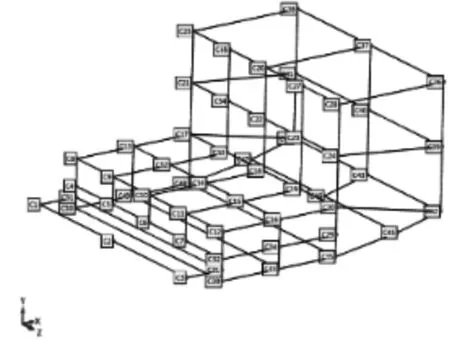
图4 砂轮架测点编布置

3 模态试验结果

在DHDAS测试系统软件中建立磨床整机和砂轮架的线框图，并导入各个测点的响应数据。首先采用海宁窗对时域曲线进行滤波，然后利用自互功率谱法对测试数据进行参数识别得到磨床的模态参数。最后利用MAC评价试验振型的正交性，对试验测试结果的可靠性进行验证。

由整机的测试数据可得到整机的前5阶模态参数，结果如表2所示。前5阶振型图见图5。

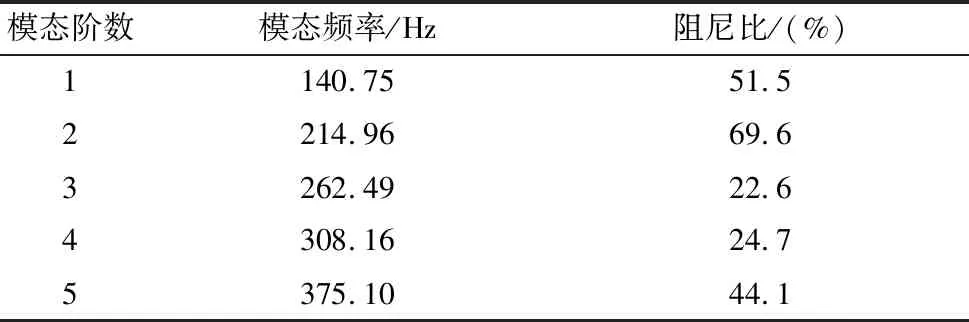
表2 磨床整机的模态参数

图5 磨床整机前5阶振型

可以发现当砂轮架上受到激励时，整机的响应基本集中在砂轮架附近，而其他部分的响应非常小。这是因为整机的刚度很大而施加的激励太小，只能在砂轮架附近出现局部响应，因此砂轮架刚度是整机构造的关键点，对磨床进行优化改进时可进一步对此进行加强。而且由于随动磨床的连接部件较多、同时连接方式也比较复杂，导致相应模态频率对应的阻尼较大，给识别带来较大困难。

对于砂轮架的测试数据，为了分别研究砂轮架在3个坐标轴方向上的振动情况，将3个坐标轴方向的数据分开处理，分别求得其前5阶的模态参数，结果如表3～表5所示。3个方向上的振动情况见图6～图8。

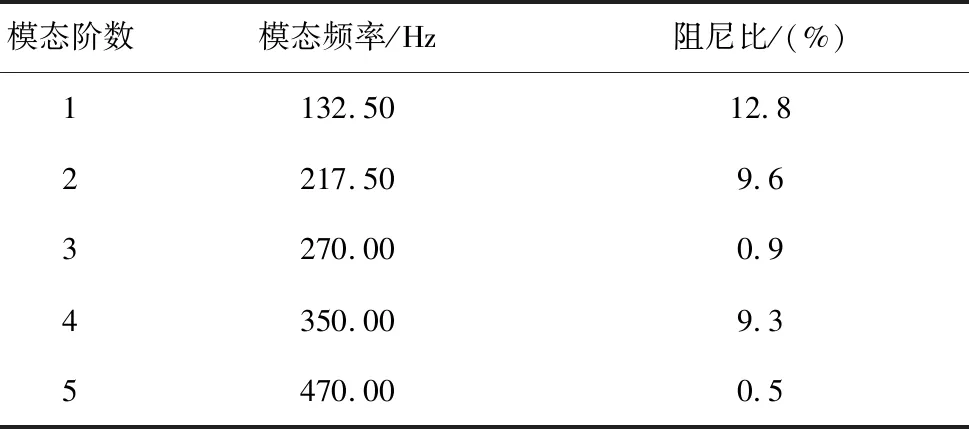
表3 大砂轮架的模态参数-X方向

图6砂轮架X方向的前5阶振型和X方向振型的振型相关矩阵

图6中标注了排除部分异常测点之后，前5阶振型中出现较大变形的测点，图7、图8中的标注相同。分析这些测点可知，在各阶振型中，砂轮架的上部出现沿着X方向的剪切振动，在Y方向的不同高度上出现反相振动。相对于砂轮架上部，下底板振动不大，仅发生了很小的翘曲变形。

表4 大砂轮架的模态参数-Y方向

图7 砂轮架Y方向的前5阶振型和Y方向振型的振型相关矩阵

在第1阶振型中，砂轮架的上部和下底板都发生了沿Y方向的弹性振动。各阶振型在Z方向的不同高度上出现反相振动但仍以同相振动为主，且相对于砂轮架上部，下底板振动不大。

表5 大砂轮架的模态参数-Z方向

图8 砂轮架Z方向的前5阶振型和Z方向振型的振型相关矩阵

在第1阶振型中，砂轮架的下底板出现沿着Z方向的反相振动。在后4阶振型中砂轮架上部出现了翘曲变形，且相对于砂轮架上部，下底板变形较小。

综合3个方向的振型可以发现X、Y方向的模态频率非常接近，Z方向上的模态频率除了第一阶以外均明显大于X、Y方向的模态频率。在3个方向中，X方向的振动相对于Y、Z方向更为剧烈，出现了反相振动，因此X方向是砂轮架的薄弱方向，在后续改进中需要对X方向进行加强。综合3个方向的振型，相对于下底板，砂轮架上部振动更为剧烈，这是砂轮架的结构薄弱点。

在X、Y方向的振型相关矩阵中，除主对角元素之外，其他元素的值都很小，在Z方向的振型相关矩阵中，除个别非主对角元素稍大外，其他非主对角元素的值都很小，说明试验的模态结果是可靠有效的。

4 结论

本文采用环境激励的模态分析方法对高精度随动数控凸轮轴磨床整机和砂轮架进行模态试验，研究其动态特性，研究工作包括：

(1)通过模态试验，得到磨床整机的固有频率、阻尼比和模态振型；

(2)由整机的模态试验结果的分析得出了砂轮架是整机结构的薄弱点，在加工过程中振动较为剧烈，如果需要进一步提高磨床的加工精度应对砂轮架进行设计改进；

(3)对磨床的砂轮架进行了模态试验，进一步研究其动态特性，由试验结果分析得到砂轮架的上部振动较大，且在3个方向中X方向即砂轮与工件接触方向上的振动最为剧烈，应在后续机型改进中予以加强。