桉树人工林抚育间伐调控技术研究
2019-04-08许晓东刘丽婷邓海燕莫晓勇
许晓东,刘丽婷,邓海燕,江 瑶,莫晓勇
(1.华南农业大学 林学与风景园林学院,广东 广州 510642;2.江西省林业科学院,江西 南昌 330013)
现代森林经营最有效的工作指南是量化描述林分结构[1]。林分结构分空间结构和非空间结构。相比起林分非空间结构,林分空间结构依赖于每株树木的大小及空间位置[2],量化林分结构特征[3],能更准确反映经营措施对林分结构的影响[4]。单木的空间指标强调的是单木与其相邻木分布格局、相对大小等的关系。而基于相邻木关系的方法可以量化林木的微环境,优于点格局的方法[5]。经研究表明参照树与其4株最近相邻木组成的5株树结构体[6],描述林分空间结构效果最佳。
近年来关于林分结构的研究多集中在对林分空间的分析与优化。贺姗姗[7]运用Ripley’s K(d)函数和大小比数、角尺度等分析人工林的林分空间格局,研发出适用于我国的林分模拟原型系统。张建华[8]以京津冀地区分布的4种华北落叶松典型林分类型为研究对象,从树种组成、直径结构、角尺度、大小比数、混交度等方面分析,构建出最优林分类型,提出了华北落叶松典型林分的近自然经营技术。吕忠爽[9]等以大小比、角尺度等8个林分空间结构指标构建综合采伐指数,通过对比各林分不同采伐强度的模拟采伐,筛选出各样地最适宜的采伐强度。G Gao等[10]以角尺度、大小比数和混交度等指标分析经营措施对油松人工林空间结构的影响,经过间伐和补植等改造措施后发现开敞度和混交度的变化最大。曹小玉等[11]综合开敞度、大小比数、交角竞争指数等6个子目标提出评价指数,并以评价指数值将杉木人工林划分为5个评价等级。可见林分空间结构参数可以精确描述天然林和人工林的林分空间结构特征,对分析、研究和调控林分结构具有重要作用。
近年来桉树人工林集约经营强度日益加大,大面积桉树纯林引起的地力下降及其他诸多生态问题更为明显[12]。对桉树人工林的空间结构进行分析,提出改造措施以优化林分结构,是解决桉树人工林地力衰退等诸多生态问题的技术措施之一。对桉树人工林林分结构的研究多为直径[13-14],树高分布[15]等非空间结构的研究。对桉树人工林林分空间结构的研究鲜有报道[16]。因此,本研究以国营雷州林业局纪家林场1~5年生的桉树人工林为研究对象,分析其空间结构特征,并提出间伐优化模型,为桉树人工林内部结构调控,提高森林质量提供技术依据。
1 材料与方法
1.1 试验地概况
纪家林场(109°42′~ 110°23′E,20°26′~21°11′N)位于广东省雷州半岛,属南亚热带湿润性季风气候,土壤为浅海沉积物砖红壤;年平均气温22 ℃,最高和最低气温分别为38.5 ℃和1.1 ℃;年降水量1 711.6 mm,相对湿度84%。
调查时间2017年6月,选取1~5年生尾巨桉无性系DH32-29纯林,每个林龄抽取6块样地,共设置了30块调查样地,进行外业调查。
1.2 样地设置
用典型取样法设置样地,每个调查样地大小为20 m×20 m,以样地的西南角作为坐标原点,测量该单元内每株树木的X、Y坐标及其树高、胸径。数据分析时统一换算样地相对坐标,缓冲区为3 m。具体样地概况见表1。
1.3 研究方法
1.3.1 林分结构研究
以 Normal、Weibull、Gamma、对数正态、Logistic等经验分布函数分别拟合林分直径分布。并对拟合后的理论株数与实际株数作x2检验和kolmogorov-smirnov检验。分析不同林龄的桉树人工林的大小比数、角尺度、开敞度、竞争指数等林分空间结构特征。
1.3.2 建立林分间伐模型
林内所有单木的大小比数、角尺度、开敞度、竞争指数和材积的算术平均值即为林分相应指标值。模型的建立采用乘除法[17]对各个空间结构参数进行多目标规划。如:x是决策向量,当在m个目标f(x1)…f(xm)中,有k个f(x1)…f(xk)要求实现最大,其余f(xk+1)…f(xm)要求实现最小,同时所有目标f(x1)…f(xm)>0,采用作为目标函数,结合了5个方面的目标函数值更能全面科学地定量描述林分结构与质量[18]。
在计算目标函数时,将角尺度Wi∈(0,1]范围的所有数据同时减去0.5,并取绝对值,角尺度的所有数据取值范围变为Wi∈(0,0.5],最优值就是接近0的最小值。综合5个子目标,确定目标函数Q(g)的计算公式如下:
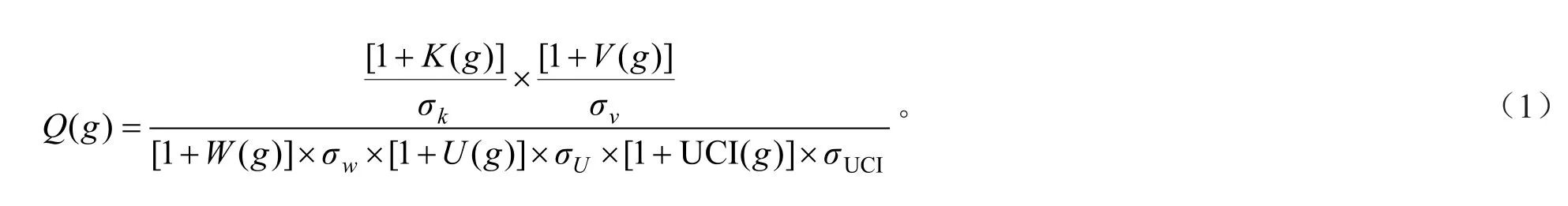
式(1)中:g为间伐后的保留木。W(g)、U(g)、UCI(g)、K(g)和V(g)分别为间伐后的林分角尺度、大小比数、竞争指数、开敞度和平均材积。σw、σU、σUCI、σK和σV分别表示林分角尺度、大小比数、竞争指数、开敞度和材积的标准差。

表1 样地概况Table1 General situation of the plots
采用Monte Carlo法解目标函数,限定采伐量(采伐木数量不超过采伐量)和运行次数(每次运行随机选取采伐木,即采伐方案),每次运行后计算采伐后的目标函数值。比较所有采伐方案的目标函数值,取目标函数值最大的采伐方案作为最优解的一个近似解。把目标函数Q(g)的值作为评价指数Q,Monte Carlo法求解算法步骤如下(如图1):
1)输入运行次数n,采伐量k;
2)计算林分各参数值:W,U,UCI,K,V;评价指数Q;
3)检查运行次数是否达到n次,是转第8步骤,否则转第4步骤;
4)随机选取采伐木,得到保留木向量,采伐量不超过k;
5)计算间伐后的参数值:W*,U*,UCI*,K*,V*;评价指数Q*
6)比较评价指数Q*>Q?,是转第7步骤,否则转第3步骤;
7)W=W*,U=U*,UCI=UCI*,K=K*,V=V*、Q=Q*;转第3步骤;
8)输出林分各参数值:W,U,UCI,K,V;评价指数Q。
2 结果与分析
2.1 直径结构

图1 林分间伐模型流程Fig.1 Program flow of forest stand thinning model
由5种经验分布函数分别拟合1~5年生的桉树人工林株数—直径分布,见表2。经卡方检验,1、2、3和5 a的桉树人工林的株数—直径分布呈正态分布(P>0.05,可靠性95%);kolmogorovsmirnov检验则显示2、3和5 a的桉树人工林的株数-直径分布呈正态分布(可靠性95%)。综合两种检验方法, 1年生林分用Logistic分布拟合效果最佳,2、3和5年生林分用Normal分布拟合效果最佳。4年生桉树人工林受到台风破坏严重,对各分布函数的拟合效果均不佳。从两种检验方法的P值看, Weibull和Logistic直径分布拟合效果优于Gamma和对数正态拟合分布。总体上看,Normal分布更适合桉树人工林直径分布拟合,Weibull和Logistic分布次之。
1年生林分峭度>0;2、3、4和5年生林分峭度<0;1和2年生时林分偏度<0,3和5年生时林分偏度>0,表明1和2年生时林分大部分林木胸径<平均值,而3和5年生时林分大部分林木胸径>平均值。
2.2 林分空间结构
对各林龄的桉树人工林空间结构参数进行统计,如表3所示,1~5年生的桉树人工林的林分大小比数均接近0.5。各个林龄的林分中,5年生的林分单木大小比数值为1的比例最少,为0.153 1;5年生林分的大小比数最大。

表2 直径分布拟合函数相关参数值Table2 Related parameters about fitting functions of diameter distribution
竞争指数方面,各林龄的林分竞争指数均小于0.2,且各林龄超过一半的单木林木竞争指数值0.2。1年生的林分竞争指数最小,2~5年生的林分竞争指数相差不超过8.51%。
从开敞度看,1年生林分的开敞度最大,2年生林分次之。3、4年生林分的林分开敞度均小于0.3,林木生长空间表现为不足,3年生林分开敞度小于0.2,林木空间表现为严重不足。
关于角尺度,1~5年生桉树人工林的林分角尺度分别为0.243 9、0.250 0、0.218 6、0.300 0、0.251 6,均<0.475,都表现为均匀分布。各个林龄中绝大部分单木角尺度取值0,0.25和0.5;较少单木角尺度为0.75,1~4年生的桉树无角尺度为1的单木;5年生的桉树中,只有0.98%的单木角尺度为1。

表3 各林龄空间结构参数值Table3 Spatial structural parameter values of stands with different ages
2.3 林分空间结构优化
1年生和2年生林分桉树人工林林木竞争压力相对较小,4年生林分受台风影响较为严重,影响直径分布拟合效果。故选取3年生和5年生的桉树人工林为例,以Monte Carlo法解目标函数间伐模型对林分空间结构进行优化和结构调整。控制间伐量小于等于总株数25%,强度中等[19]。
随机选取数量小于等于总株数25%的采伐木进行模拟采伐,对比每次采伐方案的目标函数值Q,并保留Q值最大的采伐方案。当运行次数n大于5 000次时,3年生林分Q值基本稳定,且Q取得最大值。当运行次数n大于5 112次时,5年生林分Q值基本稳定,且取得最大值。以此时的Q值作为接近最优解的次优解。
3年生林分中最优采伐方案需采伐104株林木(可通过X,Y坐标精确定位),仅占总株数的19.81%。5年生林分最优采伐方案需采伐85株林木,占总株数的20.58%。3和5年生林分采伐前后林分结构方面的变化见表4、图2。经卡方检验,伐后3、5年生的林分直径分布均用Normal分布拟合效果更好。综合2种检验方法,伐后3、5年生的林分直径均呈正态分布。3年生林分伐后大小比数和竞争指数分别下降了2.22%和6.40%;角尺度和开敞度分别增加了21.08%和10.27%;其中角尺的变化幅度最大,增加了21.08%;其他方面,平均材积略有上升;总体目标函数值比伐前增加39.92%。伐后5年生林分大小比数、竞争指数和角尺度分别下降了1.90%、7.21%和0.42%;开敞度和平均单株材积增加了10.36%和0.59%;其中开敞度的变化幅度最大,总体目标函数值比伐前增加41.24%。
3 结论与讨论
本研究从大小比数、角尺度、开敞度、竞争指数等空间结构参数分析1~5年生桉树人工林的林分空间结构,以各经验分布函数拟合林分非空间结构-直径分布。根据林分各结构参数,对林分结构进行优化和结构调整,建立了林分间伐最优模型,最大限度改善林分结构。由于4年生桉树人工林受到台风破坏较严重,对各分布函数的拟合效果不佳。综合χ2检验和kolmogorov-smirnov两种检验方法,其他各林龄中,Normal分布拟合直径分布的效果最佳,Weibull和Logistic分布次之;直径结构呈Normal分布的理论株数对森林经营有一定指导意义[16]。从拟合的峭度和偏度看,1年生林分直径分布比较集中,2、3和5年生林分直径分布比较分散;1和2年生时林分大部分林木胸径<平均值,而3和5年生时林分大部分林木胸径>平均值。

表4 采伐前后林分结构变化Table4 Stand structure changes before and after harvesting

图2 间伐前后林分直径分布Fig.2 Diameter distribution of stands between before and after thinning
各林龄林分空间结构方面,1~5年生的桉树人工林林木大小差异不明显,其中5年生林分的林木大小差异相对最明显;各林龄桉树人工林都是同一无性系造林,林木间的差异较小。通过林分角尺度值表明,1~5年生桉树人工林林木呈均匀分布,各个林龄中绝大部分单木位置呈均匀或随机分布;人工林的造林方式决定了角尺度的初始值,林木呈均匀分布,这是区别于天然林的一个基本特征,随着林分枯损或抚育间伐等经营措施,角尺度会产生一定变化。林木生存竞争压力方面,1~5林龄的林木总体承受的竞争压力均较小,其中1年生的林分竞争压力最小;1年生林分还未郁闭,林木生长较少受到邻木树冠的上方遮盖和侧翼挤压。2~5年生林分逐渐郁闭,林木生长受到邻木影响,林木竞争压力增加。林分开敞度情况与林分竞争压力类似,1年生林分树木生长空间很充足,随着林木生长林分开敞度逐渐减小。林分郁闭度在3年生时达到最大值,而林分开敞度在3年生时达到最小值。说明此时林木的生长空间最不足。
关于林分空间结构的优化,首先结合大小比数、角尺度、开敞度等5个参数建立目标函数。并用林分间伐模型求解。本研究以3和5年生的桉树人工林为样本对象,通过林分间伐模型输出最优间伐方案,采伐木数量各占总株数的19.81%和20.58%。通过该模型输出的方案间伐,增加了林木生长空间,降低了林分竞争水平,使得林木的分布更为均匀,林分空间结构的稳定性得到明显改善。伐后的3、5年生林分直径分布均呈Normal分布,且经卡方检验,伐后3、5年生的林分直径分布用Normal分布拟合效果更佳。
综合各个空间指标参数建立目标函数,可通过评价指数定量描述林分的空间结构稳定性。通过Monte Carlo法,建立林分间伐模型,通过模型计算出的最大目标函数值的间伐方案,为优化人工林空间结构提供了新方法。间伐后空间结构更优的3和5年生林分直径分布更接近Normal分布。林分结构稳定性与林分直径分布的关系有待进一步研究。本次研究的林分间伐模型同样适合具有生态意义的商品兼用林,通过中等或小强度间伐优化林分空间结构,提高林分结构稳定性。若培育的最终目标是桉树异龄混交林,可以结合择伐和补植耐阴树种,来增大林分混交度和林分物种多样性[20]。林分间伐模型具有灵活性,可控制采伐量,增添或减少空间结构指标重新定义目标函数。使用林分间伐模型运行所需数据较为繁杂,可以考虑结合无人机拍摄图,航拍图片数字化处理获取基础数据,再进行林分空间结构分析,从而减低成本,提高效率。
