窄线宽半导体激光器的热设计及优化
2019-04-08刘思喆全伟翟跃阳
刘思喆, 全伟,2,*, 翟跃阳
(1. 新型惯性仪表与导航系统技术国防重点学科实验室, 北京 100083;2. 北京航空航天大学 大数据精准医疗高精尖中心, 北京 100083)
半导体激光器作为原子陀螺仪中的激光泵浦光源,其热特性对仪器整体具有较大影响。伴随着半导体激光器其相关集成芯片的广泛研究与应用,其热问题一直是人们关注的焦点之一。虽然半导体激光管具有较高的光电转换效率,但工作时仍然有相当部分的电能转换为了热能,尤其是近年来,半导体可调谐激光器的设计与封装朝尺寸轻薄短小的方向发展,使得激光管发热密度上升[1],随之会出现波长红移[2]、阈值电流增加[3]、模式不稳定、光电转换效率降低[4]等问题,此外温度上升还会产生热应力,导致材料形变,影响半导体激光器的精度与使用寿命。因此研究半导体激光器的热特性,解决激光器的散热问题,提升器件的使用寿命具有极其重要的现实意义。
目前常见的半导体激光器特性热分析主要集中在激光器芯片的热效应,文献[5]对808 nm半导体激光器温度特性进行了分析,得到不同功率输出下的热阻,并分析其温度随时间的变化。文献[6-7]使用有限元分析的方法对半导体激光器进行温度特性分析的研究,能够完整了解完整装配体在整个工作时间内的温度分布云图,以及各节点温度随时间变化的曲线。在激光器热设计方面,主要针对激光器热沉进行结构设计与优化。文献[8-10]对激光器热沉结构进行了温度场分析以及结构的优化,优化后的结构能够一定程度上减小激光管内部温度的持续累积。但已有文献少有涉及到半导体激光器整体结构的热设计,而在实际使用中激光器自身热量的散失与外界环境的影响往往不能够直接作用在激光器芯片上,而是通过整体结构不断传递的结果,因此关于半导体激光器整机的热设计及其优化是很有必要的。
本文选用795 nm分布式布拉格反射激光管,首先建立了激光器整体结构的实体模型;然后结合有限元理论对热分析法进行拓展,得到理论条件下结构温度场分布,并对仿真结果进行分析,对超出预计温度的组件进行再次热设计,通过结构尺寸优化与结构形式优化2种优化方式对半导体激光器分别进行稳态和瞬态的热分析模拟实验,结合分析数据对激光器内部各组件之间的联系进行总结,并依据分析结果提出经过优化的半导体激光器散热结构。
1 模型建立
1.1 几何模型
激光器整体结构包括激光管、机械安装模块、激光准直模块、准直透镜、底座、外壳、带DB9的背板与保护电路,工装方式包括螺栓紧固等多种方式。本文选用795 nm分布式布拉格反射激光管(PH795DBR),尺寸为8.5 mm×5.8 mm×5.2 mm的长方体结构,激光管底部集成半导体致冷器(Thermo-Electric Cooler,TEC)用于激光管内部散热,同时作为激光管向外辐射的热源,功率为0.3 W。激光管与机械安装模块、机械安装模块与底座之间主要通过热传导的方式进行散热,整体结构与内部空气之间主要通过热辐射与自然对流进行散热。因此,本文在考虑机械性能的基础上,尽可能增大激光管热辐射面与机械安装模块的接触面积,同时选择散热系数较大的材料增大结构与激光器内部空气间的热辐射。在Solidworks中对激光器整体结构进行实体建模,如图1所示。为保证计算精度和提高计算速度,需要对模型进行简化处理。本文对倒角、倒圆、凸台、垫片和电路模块等对热分析影响可忽略不计的几何特征及零部件进行了合并与简化处理,如图2所示。
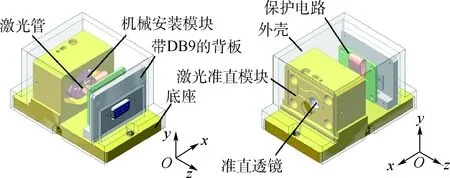
图1 实际建立的半导体激光器装配模型Fig.1 Assembly model of semiconductor laser for actual use
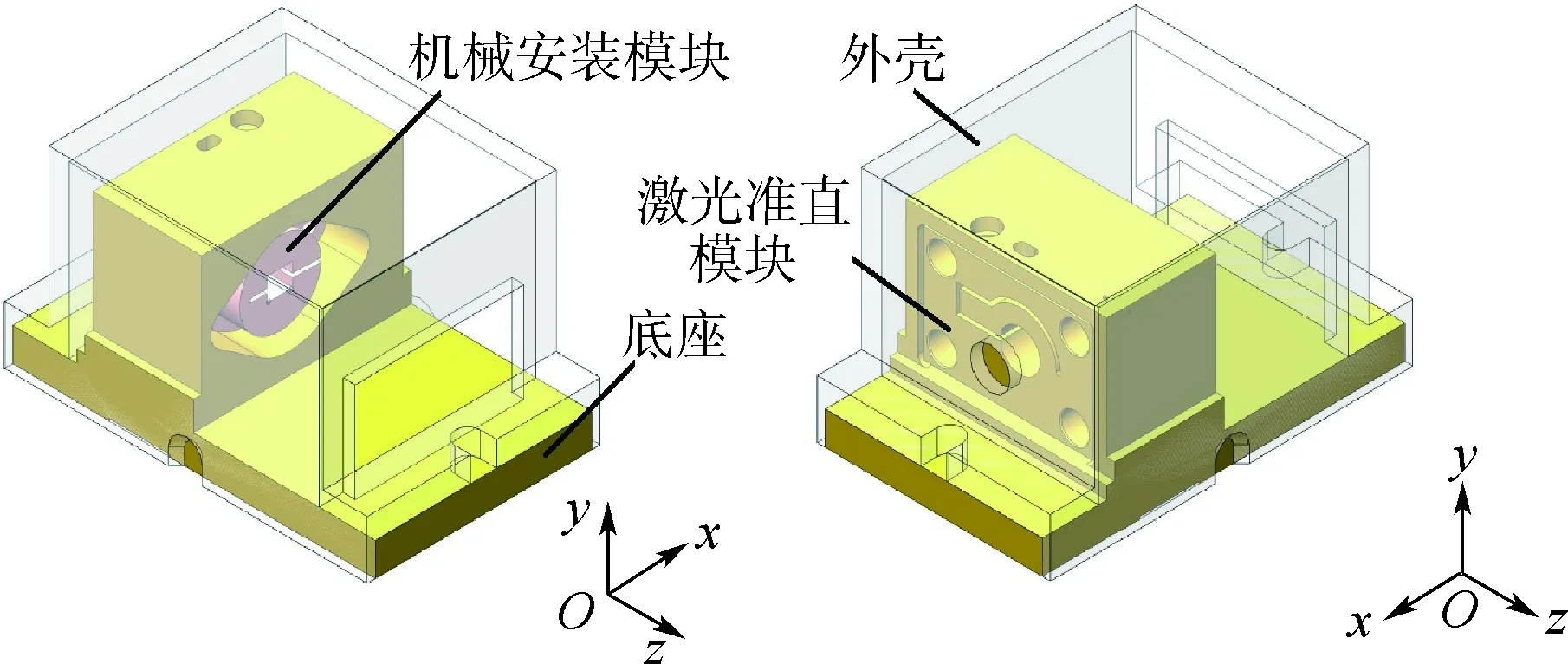
图2 用于有限元分析的半导体激光器简化模型Fig.2 Simplified model of semiconductor laser for finite element analysis
1.2 有限元热分析法
根据热力学第一定律,对于一个封闭系统,有[11]
Q-W=ΔU+ΔKE+ΔPE
(1)
式中:Q为热量;W为做功;ΔU为系统内能;ΔKE为系统动能;ΔPE为系统势能。在大多数工程传热问题中,认为ΔKE=ΔPE=0,通常也不考虑做功,即W=0,Q=ΔU。因此,可以将热分析分为稳态热分析和瞬态热分析,稳态热分析时,Q=ΔU,即流入系统的热量等于流出系统的热量,主要为获取整体结构的温度场分布;瞬态热分析时,q=dU/dt,即流入或流出的热传递速率q等于系统内能的变化。将其运用到微元体上,得到热传导的控制微分方程为[12]
(2)
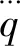
将控制微分方程转化为等效的积分形式,可得
(3)
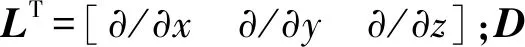
在有限元区域分解划分时,通常使用四边形和/或三角形单元处理二维模型,使用四面体、金字塔型或六面体单元处理三维模型。为保证温度在单元内部和单元边界上是连续的,选择采用多项式假设,即根据单元类型的不同,应包含不同的一次项、平方和混合的立方项,则以单元节点温度为未知数的多项式可以写为[13]
T={N}T·{Te}
(4)
式中:{N}T为单元形函数的行向量;{Te}为单元节点温度矢量。
由单元节点温度可以得出每个单元的温度梯度和热流,分别如式(5)和式(6)所示:
{a}=LT=B{Te}={L}TN{Te}
(5)
{q0}=DLT=D(B){Te}=D{a}
(6)
式中:矩阵B是通过对形函数求微分得到的,即B={L}TN。
将假设的温度变化代入积分方程,可得
{Qf}+{Qd}+{Qc}
(7)
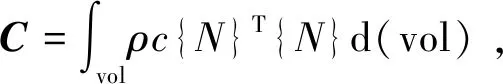
本文主要考虑稳定的热载荷对器件以及系统内部的影响,因此首先进行稳态热分析,通过有限元计算确定稳定的热载荷引起的温度、热梯度、热流率、热流密度等参数,以及确定初始的温度分布。
对于稳态热传递,热平衡的微分方程可以表示为
(8)
对应的有限元平衡方程为
K{T}={Q}
(9)
2 热分析与热设计
为保证模型的完整性,利用ANSYS与Solidworks之间的模型转换接口,将Solidworks模型导入ANSYS中进行下一步分析材料设计,材料性能如表1所示[14]。

表1 材料性能参数[14]Table 1 Performance parameter of material[14]
2.1 有限元网格划分
有限元的基本思想是把复杂的形体拆分为若干个形状简单的单元,利用单元节点变量对单元内部变量进行插值来实现对总体结构的分析,离散而成的有限元集合将代替原来的弹性连续体,根据能量守恒原理求解一定边界条件和初始条件下每一节点处的热平衡方程计算出各个节点的温度及其他相关量。因此,网格划分将关系到有限元分析的规模、速度和精度。
在建立激光器整体结构的仿真模型时,网格并不是越多越好,反之,一些零件的网格如果划分的过于细致,会导致热分析效率大大降低。因此,在保证热传递路径不受影响的情况下,应忽略一些不关注热分布的部分,采用设置热耦合的方式进行网格的合理简化[15]。
本文在处理薄板部分时使用板壳单元,将较厚的部分作为体单元处理,零件-零件的装配使用RBE2线刚性单元模拟。使用标准默认模式进行网格划分后,模型中共包含节点18 775个,单元10 692个,其中实体单元9 608个,接触单元1 084个,单元性质集3个。然而,在查看网格划分质量系数时发现,标准模式下平均网格质量系数仅为0.588 54,不满足后续计算要求(一般情况下平均网格质量系数至少为0.7),因此下一步需检查出网格质量较差的部位进行更加精细的手动网格划分,经过分析Mesh Metric提供的数据可以得到不同网格质量在整体结构中对应的位置,其中网格质量为0.5在整体结构中对应的位置如图3所示。利用同样的方法可以得到网格质量低于网格质量为0.7对应的所有位置,如图4所示。
通过网格质量系数可以看出质量较差部位集中在外壳外包络面、透镜安装模块与机械安装模块前端部分,因此,手动设置以上3部分的网格划分尺寸,分别为3、1.5、1 mm。优化后的有限元节点个数为136 361个,单元个数为90 557个,其中,体单元84 883个,接触单元5 674个,单元性质集3个,网格质量0.805 98,半导体激光器用于热分析的有限元结构模型如图5所示,各部分网格划分情况如表2所示。
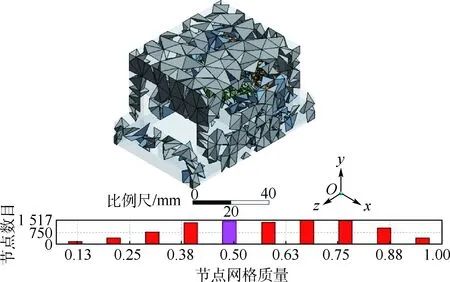
图3 网格质量为0.5在整体结构中对应的位置Fig.3 Position in overall structure with mesh metric of 0.5
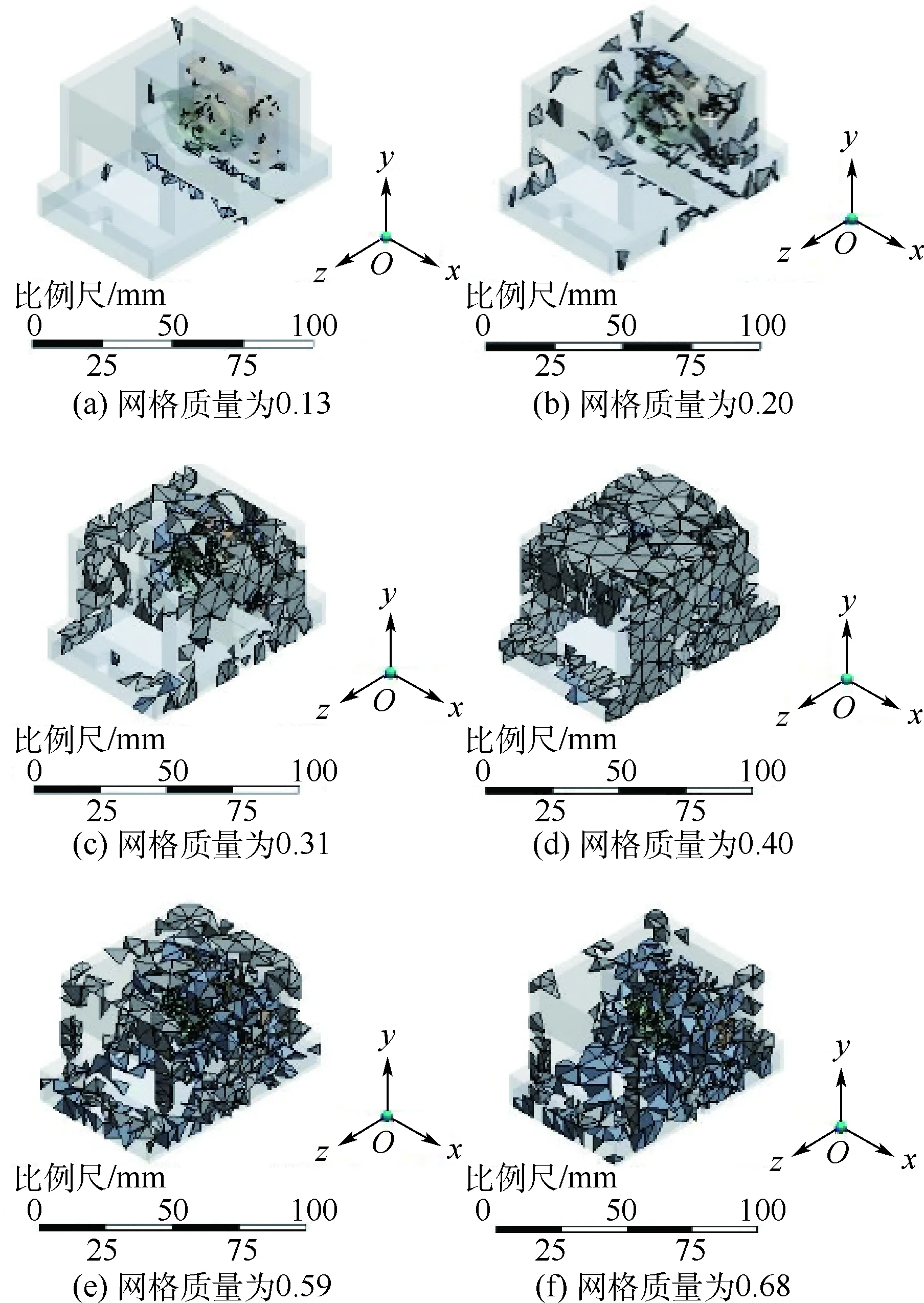
图4 网格质量低于0.7在整体结构中对应的所有位置Fig.4 All positions in overall structure with mesh metric under 0.7

图5 半导体激光器的有限元模型Fig.5 Finite element model of semiconductor laser

名称节点单元整体结构13636190557底座2005913188激光准直模块3948925104机械安装模块4927732078外壳2753614513
2.2 假设与解析条件
为简化计算,本文在对激光器整体结构内部温度场分析时,给出如下的假设与解析条件:
1) 激光管在整个计算过程中保持平稳运行,内部集成的TEC正常工作,产生的热通量在计算过程中保持恒定不变。
2) 空气与外壳接触面上的传热为标准对流换热,各壁面的边界条件只考虑热通量和温度2种边界条件,忽略各壁面上的辐射传热。
3) 外壳内部的空气密度保持恒定,不因温度变化而改变。
4) 激光管底部与机械安装模块之间涂抹导热硅脂,认为TEC底面产生的热全部传递到与其直接接触的机械安装模块内部底面上,经过实验测定TEC产热功率为0.35 W。
5) 外壳与空气对流换热系数设置为系统默认的Stagnant Air-Simplified Case,环境温度设置为22℃。
6) 以实际使用时的工况作为参考,设置激光器底座与实验平台接触面的边界条件为固定支撑。
2.3 热分析结果
图6为半导体激光器整体结构的稳态温度场梯度云图(为了更好地展示结果,隐藏外壳部分)。图7截取了前100 s整个装配体瞬态温度随时间变化的曲线。
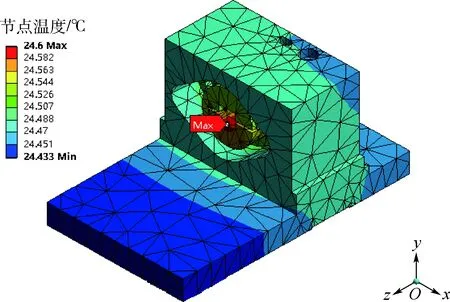
图6 半导体激光器结构温度场分布云图Fig.6 Contour of temperature field distribution of semiconductor laser structure
从图6的仿真结果中可以看出,基于2.2节假设与解析提出的条件,整体结构最高温度主要集中在机械安装模块与底座部分,达到24.6℃;整体最低温度位于底座底面,为24.433℃,相比于环境温度有2.4℃以上的温升(环境温度假设为22℃)。如图7所示,曲线呈现温度上升趋势的范围很小,即在接通电源的很短时间内温度升到最大值,这也从侧面反映分析整体温度场分布并进行散热结构优化的必要性,有可能在接通电源的瞬间激光管就会由于散热不利而被烧坏。
机械安装模块与外壳之间存在一定的空隙,增加了一部分的空气对流用于散热,也在一定程度上隔绝了电路模块元器件发热对整体结构温度场的影响。为简化分析,上述分析中忽略电路板散热,实际温度应比上述仿真分析温度更高,温升会导致一定的热膨胀,从而产生较大的热变形,热变形不仅对激光管施加不均匀挤压导致激光管寿命缩短,也会影响热流密度在结构上的分布,导致散热变差。图8给出了主要散热结构机械安装模块和底座的温度随时间变化的曲线,黑色曲线为未产生频移的光谱机械安装模块的瞬态温度变 化,红色曲线为底座瞬态温度变化。从图中不难看出,机械安装模块的整体性能明显优于底座,单独的底座并不能实现温度控制的目的。因此后续设计有必要针对底座进行结构优化和装配方面进行优化设计。
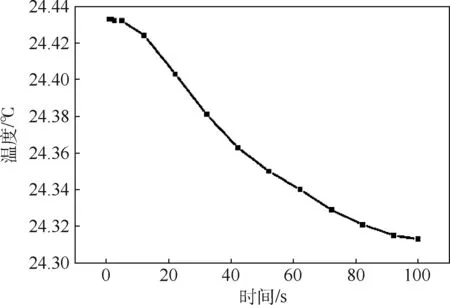
图7 瞬态温度随时间的变化Fig.7 Change of transient temperature with time
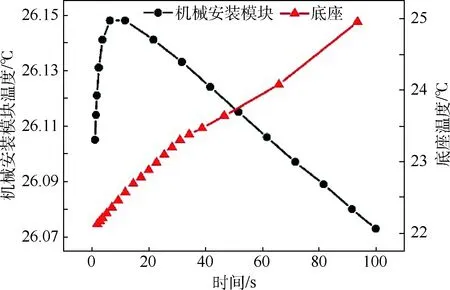
图8 机械安装模块与底座瞬态温度变化Fig.8 Transient temperature change of mechanical installation module and base
3 优化方案与分析
3.1 优化方案
机械安装模块热设计的目的主要是增大激光管的散热,尽可能削弱由于热膨胀导致的热变形。本文提出2种优化思路:①基于现有结构,改变机械安装模块的尺寸、材料等参数;②重新进行机械安装模块结构的设计。分别对上述方案进行温度场仿真,并对优化结果进行分析。
依据文献[16-17]提出的数学模型,为了能够使散热片在有限空间中的散热性能达到最好,应确使散热片中温度最高的节点温度尽量最小,构建几何平均温度为目标函数的散热结构拓扑优化模型:
(10)
式中:X为设计向量;下标G表示几何平均温度;Ω为散热结构所占的区域;T(x)为设计域中节点x的温度;|Ω|表示整体结构的体积;n为凝聚因子,其取值越大,表示几何平均温度越接近于最高温度,针对本文的窄线宽半导体激光器算例,n的均值取20。当采用有限元的方法进行求解时,几何平均温度fG(X)可表示为节点温度的形式:
(11)
式中:Ni、Ti和Ωi分别代表第i个单元的形状函数矩阵、节点温度阵列和区域。
为到达散热器散热效果的最大化,采用的优化参数选择方法为节点温度最小化方法,可用式(12)描述:
(12)
式中:TMP(X)为优化的目标函数,即散热片中温度的最高节点温度值;m,a,b均为常量;在本案例中,x1为底座的厚度;x2为底座底板的长度;x3为底座上用于安装激光管部分的槽体宽度。通过仿真的方法,发现改变底座高度的方法更简便有效。
3.1.1 结构尺寸优化方案
2.1节中提到,仿真时忽略了电路板的散热对整体热场的影响。为了进一步降低电路板元器件散热的影响,选择采用电路板外置的方式,这样可以减小底座底板的长度,但随之而来会减小底板的散热面积,因此考虑增加整个底座的高度,避免散热效果受到巨大影响。结构尺寸优化方案设计如图9所示。用于有限元分析的简化模型在相同解析条件下的稳态温度场分布如图10所示。
图9 结构尺寸优化后的半导体激光器装配模型Fig.9 Assembly model of semiconductor laser after structural size optimization

图10 结构尺寸优化后的稳态温度分布云图Fig.10 Contour of steady-state temperature distribution after structural size optimization
3.1.2 结构形式优化方案
根据文献[18-19],由于PH795DBR激光管有源层的长方形结构特性导致直接输出光束形成与其他激光极为不同的远场特性,即其输出激光具有高发散特性,且垂直于结平面的发散速度快,发散角较大,平行于结平面的发散速度慢,发散角较小,二者差异约为12°~60°。因此在半导体激光器的实际应用中,对其光束的准直和整形以提高其光束质量是一件非常重要的事情。通过对比常见激光整形方案,本文选择处理光束圆形度能力较强的变形棱镜对进行激光整形,保证输出光束的M2参数和波前误差更具有优势。在这种准直模式下,采用激光管竖直安装的方式如图11所示(外壳未展示),此结构更加小型化,各部件之间也更加紧凑。仿真分析时对结构中的倒角、倒圆、凸台等进行了简化,棱镜台仅提供棱镜对的支撑与固定功能,拟采用导热系数很小的超稳材料,因此在稳态温度场分析时也忽略不计。简化模型在相同解析条件下的稳态温度场分布如图12所示。
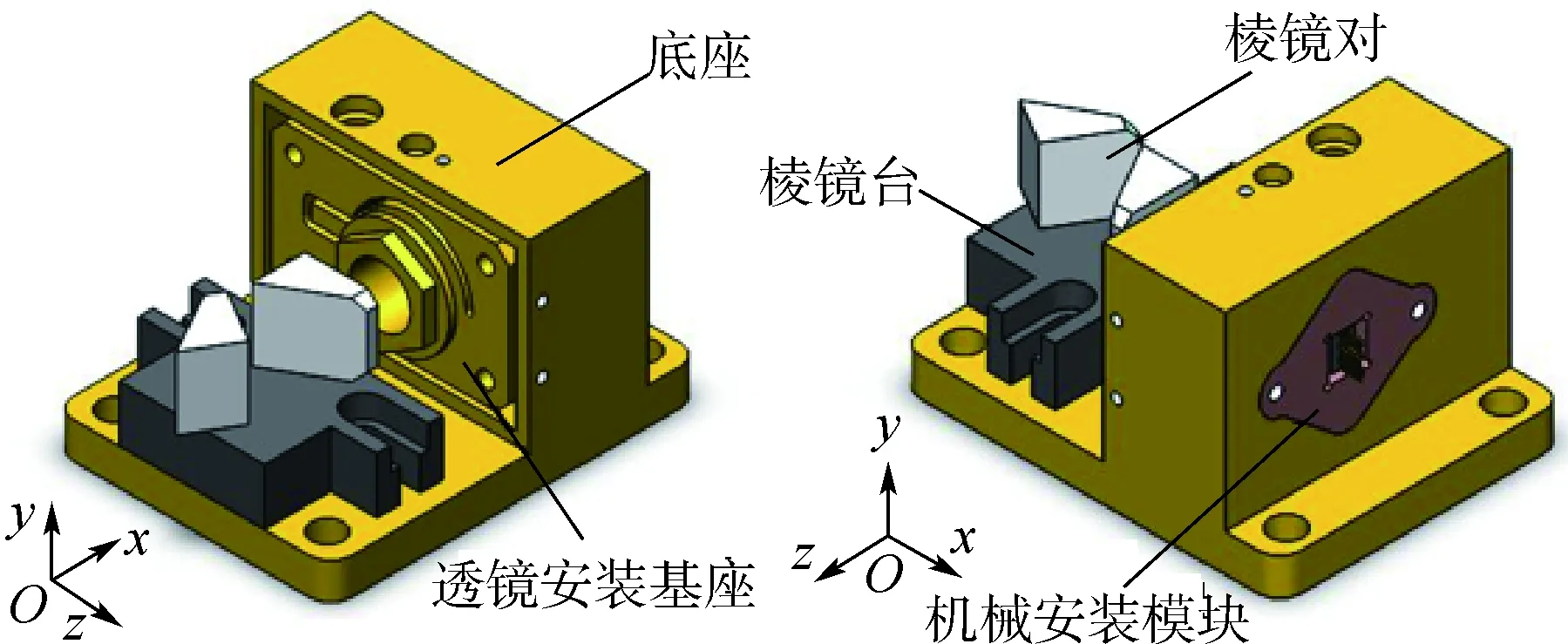
图11 结构形式优化后的半导体激光器装配模型Fig.11 Assembly model of semiconductor laser after structural form optimization
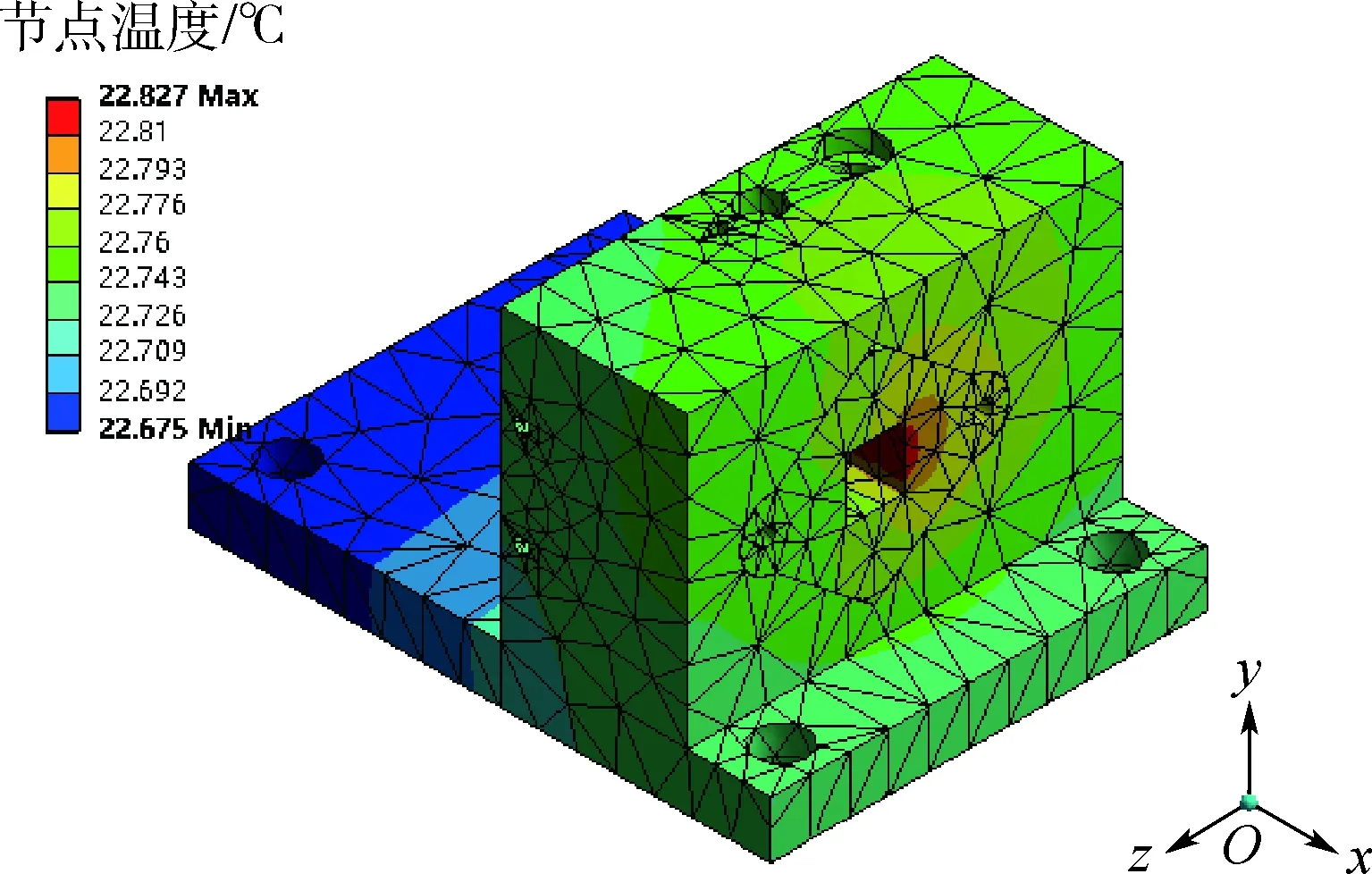
图12 结构形式优化后的稳态温度分布云图Fig.12 Contour of steady-state temperature distribution after structural form optimization
3.2 结果分析
由图10可以直观地看到,结构尺寸优化模型底座的温度分布更加均匀且温度梯度更大,但是仿真结果显示模型稳态的最低温度为24.931℃,与室温相差为2.9℃,最高温度为25.093℃,这一结果比没有优化之前的温差更大,显然,想要通过减小底座地板长度,增大整体高度的方案不可行。分析其中的原因,底板距离热源更远,在同样条件下能够承担更多的散热功能。
由图12能够看出,结构形式优化后的整体温度梯度变化相较前两者稍有不足,但整个装配体的最高温度只有22.827℃,与室温相差仅为0.827℃,明显优于初始方案与尺寸优化方案。为了更直观地对结构参数优化方案与结构形式优化方案进行比较,对2个方案分别进行了瞬态温度场分析,检测了整个装配体前100 s内瞬态温度随时间变化的规律,并绘制曲线如图13所示。
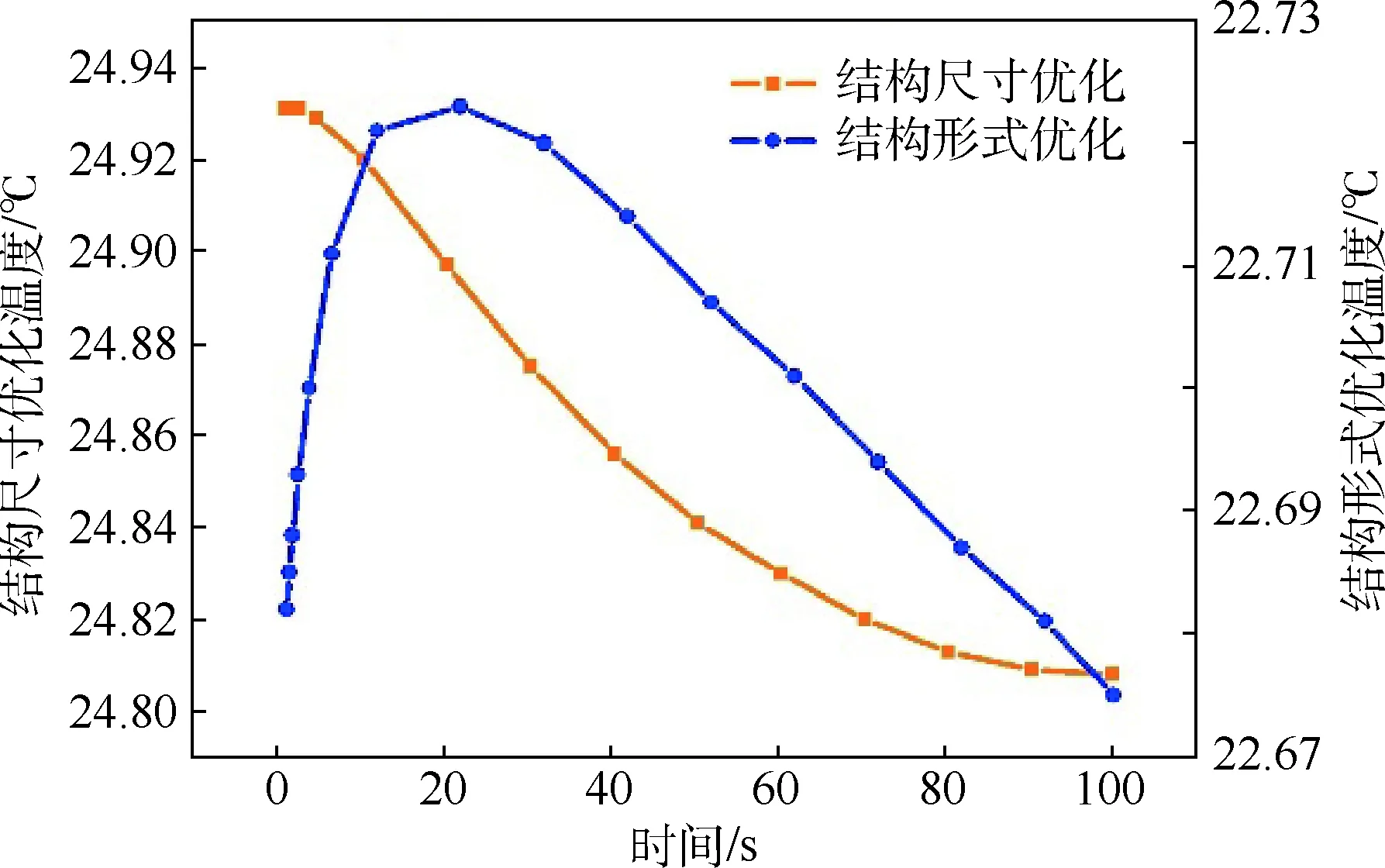
图13 结构尺寸优化方案与结构形式优化方案在前100 s内的瞬态温度变化Fig.13 Transient temperature change of structural size optimization scheme and structural form optimization scheme in the first 100 s
由图13可以更加直观地看出,蓝色曲线呈现出上升趋势的时间明显长于橙色曲线,也就是说结构形式优化方案能够在通电瞬间,对激光管的温度上升实现更好的控制,不至于在通电瞬间的开关电流对激光管进行损坏。
4 实验对比
为验证热设计的正确性与可行性,以及热分析计算的准确性,激光机加工采用结构形式优化结构,在实验室环境下进行了温度测试,通过实验数据可以修正热分析模型,指导后面的优化设计方案。
参考激光管PH795DBR的数据手册,给定输入电流为80 mA,此时激光管的输出功率约为0.35 W,在实验室环境下对激光器进行连续100 s温度测试,结果如图14所示。
由图14可得,实验开始的前50 s内温度处于上升的趋势,且最高温度在22.75℃附近,之后温度开始下降,并在80 s之后基本稳定在22℃左右。实验结果与仿真结果一致性良好,但存在偏差,分析原因如下:①实验中由于其他设备工作时采用风扇散热,引起实验台空气流速增大,空气对 流换热系数无法完全模拟仿真时设定的5 W/(m2·℃),根据式(2)媒介传导速率在一定程度上会影响热传导;②在实际使用时,室温并不是恒定不变的,这导致稳态温度会出现波动;③出于对激光管的保护,实验中并没有将80 mA的电流直接加载到激光管上而是逐步加大,这导致温度上升较慢且用时较长。
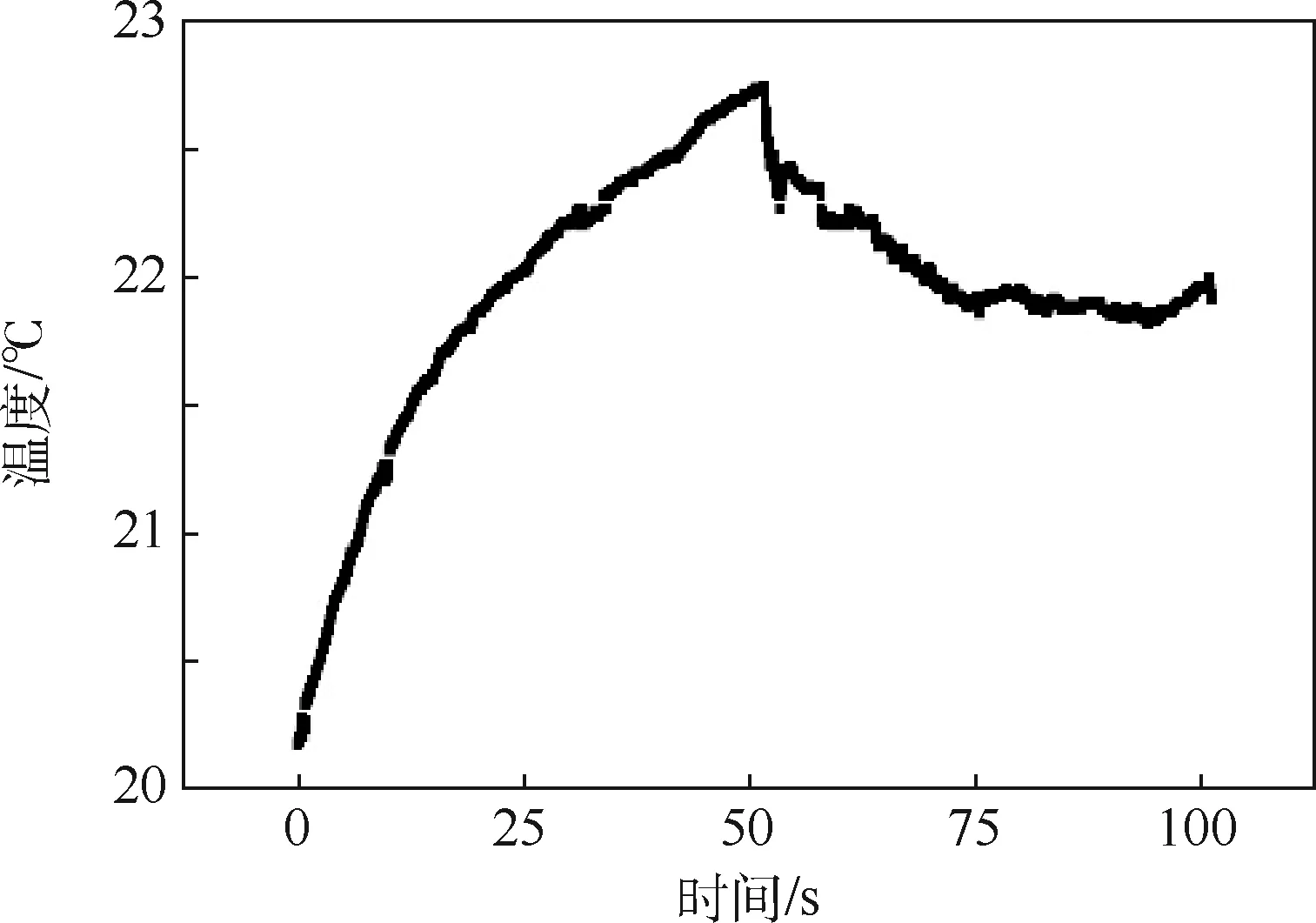
图14 结构形式优化后的结构在实验室环境下前100 s内的温度变化Fig.14 Temperature change of optimized structural form in laboratory environment in the first 100 s
5 结 论
为了保证激光器在实验室环境下正常可靠的工作状态,对激光器装配模型进行了基于有限元的热仿真分析,并基于保护激光管的考虑,引入了2种热设计优化方案。
1) 本文对激光器进行稳态以及瞬态温度场分析,得到稳态时最高温度达到24.6℃,长时间的温度累计容易引起机械材料一定的热膨胀,从而产生较大的热变形,热变形不仅对激光管施加不均匀挤压导致激光管寿命缩短,也会影响热流密度在结构上的分布导致散热变差。
2) 根据前100 s内机械安装模块与底座的瞬态温度变化曲线,给出2种优化方案:结构尺寸优化方案和结构形式优化方案,2种方案均能够改善稳态温度场分布的均匀性。
3) 结构形式优化方案的散热效果明显,温差由原来的2.9℃降低到0.8℃,并通过温度测试实验验证结构形式优化后的激光器具有更好的散热性能。
