基于切换系统的变体飞行器鲁棒自适应控制
2019-04-08梁小辉王青董朝阳
梁小辉, 王青,*, 董朝阳
(1. 北京航空航天大学自动化科学与电气工程学院, 北京 100083;2. 北京航空航天大学航空科学与工程学院, 北京 100083)
变体飞行器是一类极具发展潜力的现代新型概念飞行器,可通过改变自身的气动外形来适应不同的飞行环境、剖面和任务,确保整个飞行过程的最优飞行效能[1-2]。因此,相比于传统飞行器,变体飞行器具有更大的飞行包线和更好的环境适应能力[3],具有广阔的应用前景和重要的研究价值。但是,由于其强不确定性和复杂多变的气动特点给飞行控制系统的设计带来了巨大挑战,一直受到国内外许多学者的关注[4-6],是当前航空航天领域的研究热点之一。
目前,针对变体飞行器快速变形过程中的飞行控制系统设计问题,主要采用鲁棒控制、自适应控制和滑模变结构等方法。为保证变体飞行器变形过程的稳定性,文献[7]设计了一种基于自适应神经网络修正的动态面控制方法,解决了控制系统输入、输出受限和反步法中存在的“指数爆炸”的问题。考虑到变体飞行器受外部干扰和不确定性影响严重,气动特性复杂的特点,文献[8]设计了一种带指令滤波的鲁棒控制器,保证了系统具有良好的跟踪性能,且跟踪轨迹光滑不存在跳变。但是,由于变体飞行器是一个复杂的非线性系统,其变形过程存在严重的外部干扰,上述文献多采用几种控制方法相结合的思想,这就导致其控制器设计过程显得异常复杂。
切换系统作为一个处理复杂系统的有效工具,可将一个复杂的非线性系统转化为若干简单子系统切换,这为解决变体飞行器控制系统设计问题提供了一条有效途径,近年来受到了国内外许多学者的关注[9-12]。文献[13-16]构造了一类切换线性变参数(LPV)模型,在真实反映变体飞行器动态特性的同时,将变体飞行器这一复杂系统转化为线性切换模型,简化了飞行控制系统的设计过程。考虑到变形过程中存在的异步切换问题,文献[15]设计了一类H∞鲁棒控制器保证了控制器异步情况下系统的稳定性。针对变体飞行器切换过程中存在的系统状态跳变问题,文献[16]提出了一种基于平滑过度的切换控制策略,成功抑制了切换过程中的状态跳变,实现了整个变形过程的平稳光滑切换。但是以上针对变体飞行器的切换控制方法,并未考虑实际飞行中存在的强不确定性与外部干扰。
本文主要针对一类后掠角可变的变体飞行器飞行控制问题展开研究。利用切换系统理论,将变体飞行器复杂的气动模型转换为了线性切换系统,在真实反映其变形动态特性的基础上,降低了整个飞行控制系统设计的复杂程度。考虑到变形过程中存在的严重不确定性和外部干扰,提出了一种改进的鲁棒自适应更新律,克服了参数更新对模型的依赖,降低了系统不确定性和外部干扰的影响。利用变形序列已知的特点,设计了一种模型依赖平均驻留时间切换控制律,保证了系统整个切换过程的最终一致有界(Ultimate Uniformly Bounded,UUB),并降低了方法的保守性,确保系统能够快速切换。通过仿真验证,证明了本文方法的有效性。
1 变体飞行器建模与分析
本文主要以美国NextGen 航空公司设计的“火蜂”(Teledyne Ryan BQM34 “Fire-bee”)变体飞行器为研究对象,其结构如图1所示。“火蜂”变体飞行器是一款变体飞行技术验证机,为适应各类任务需求,如亚音速或超音速飞行、侦查和战斗等,其机翼后掠角可在一定范围内连续变动[1,14],以此来改变飞行器的气动与飞行性能,实现“巡航”、“高速”、“标准”和“机动”等多种构型。由于其在飞行过程中的外形变化会引起质心位置、转动惯量、翼展与面积等多种构型参数的变化,还会引起气动力和惯性力的非线性变化,给飞行器的控制器设计带来了巨大挑战。
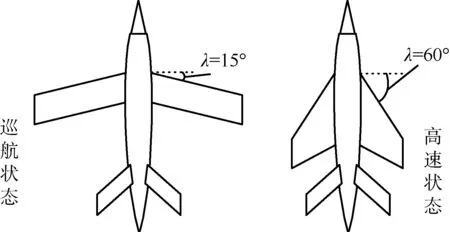
图1 变体飞行器结构[1,14]Fig.1 Structure of morphing aircraft[1,14]
“火蜂”变体飞行器在变形过程中机翼后掠角λ的变化范围为15°~60°(其中15°对应“巡航”状态,60°对应“高速”状态),且平均气动弦长、机翼面积和机翼展长等参数随机翼后掠角连续变化,重心位置可通过机身的配重自动调整,其他构型参数可参考文献[17]。根据牛顿-欧拉法,“火蜂”变体飞行器的纵向短周期非线性动力学模型为[1]
(1)

(2)
利用小扰动线性化方法对系统(1)进行线性化处理。选取高度H=9 144 m、马赫数Ma=0.5作为配平点,可以获得不同机翼后掠角(λ=15°,30°,45°,60°)下的变体飞行器纵向短周期线性模型:
(3)
式中:
为描述简单,将上述系统改写为

(4)

根据切换理论,飞行器的整个变形过程,即机翼后掠角由15°变化到60°,可以被描述为一个线性切换系统:
(5)
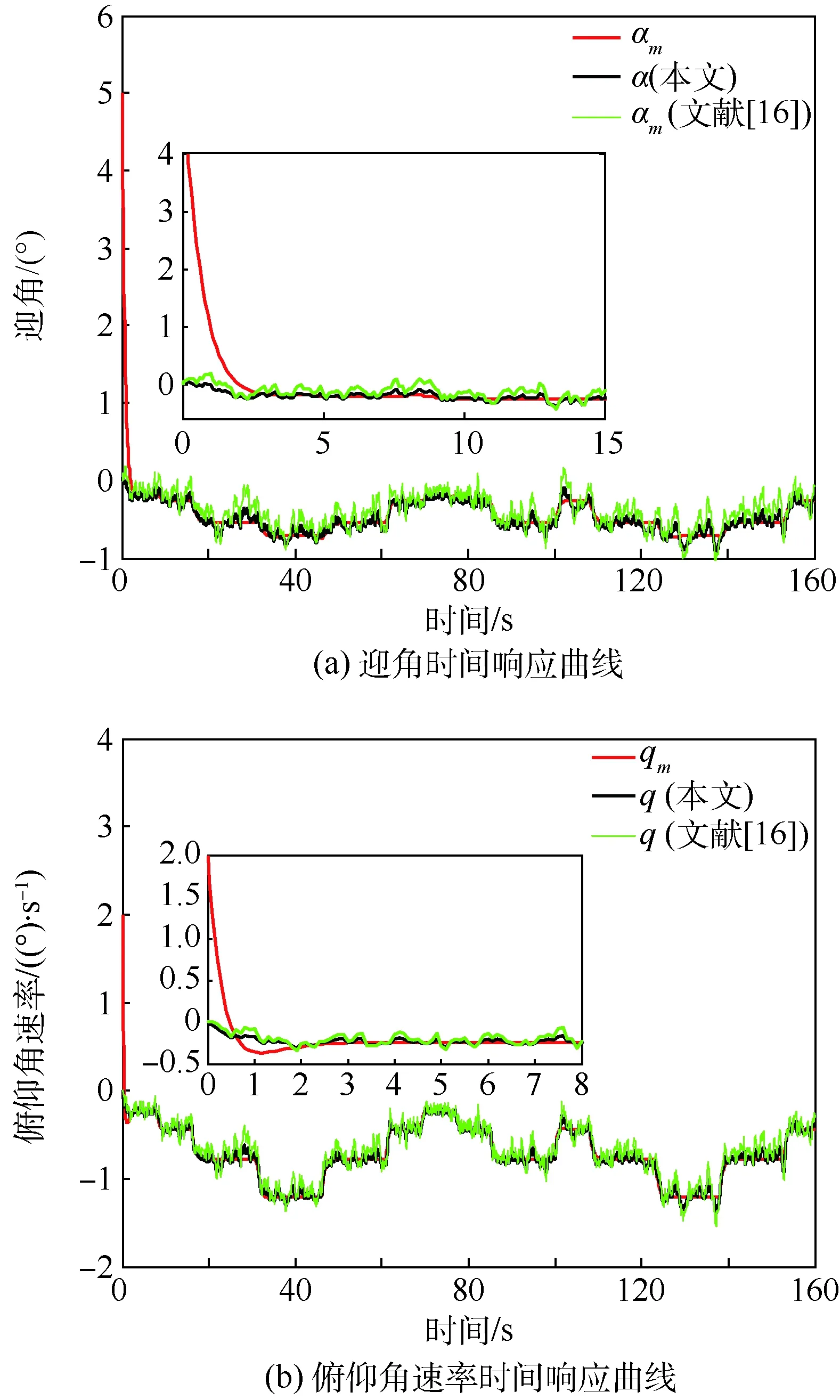
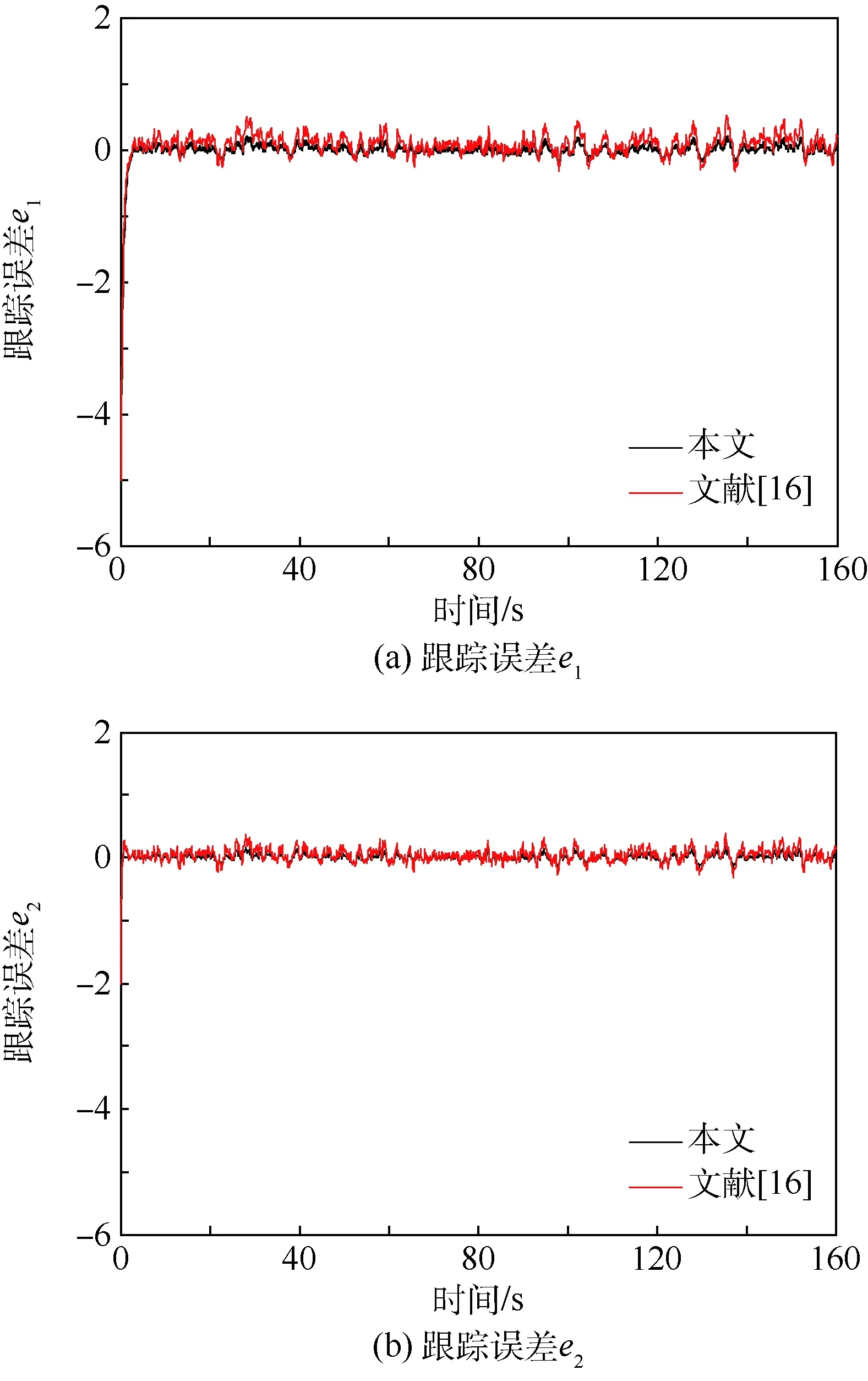
式中:切换律σ(t)是一个分段右连续的常值函数,每个切换瞬间可在有限集Ω={1,2,…,m}中取值,m为子系统总数;对于时间序列{t0=0 考虑到变体飞行器系统的复杂性,系统(4)在线性化处理时不可避免的忽略了一些结构参数摄动和环境不确定因素的影响。因此,该系统必然存在一定的未建模动态和外部干扰,即获得的模型(5)是一个受外部干扰的不确定线性切换系统。 现给出一些必要定义和引理。 引理1[19]令常数φ∈Rg,φ∈Rs,W∈Rg×g,V∈Rg×s,其中,φ、φ、W和V是常数矩阵,则下列不等式成立: 2φTWVφ≤φTWWTφ+φTVTVφ 对于变体飞行器的不确定线性切换系统(5),给出切换参考系统(5)为 (6) 式中:xm为期望的状态变量;r为有界参考输入;Amp和Bmp是已知矩阵,且矩阵Amp,∀p∈Ω是Hurwitz的。为使得系统(5)能够跟踪给定的参考模型(6),构造如下的状态反馈控制器: (7) (8) (9) 结合上述讨论,本文的主要目的是:针对存在不确定性和外部干扰的变体飞行器线性切换系统(5),设计状态反馈控制器(8)和切换控制律σ(·),使得变体飞行器在变形过程中能够精确跟踪参考模型并具良好抗干扰能力。 根据多变量自适应理论[20],给出如下的假设。 假设1存在矩阵Sp,p∈Ω,使得矩阵Mp满足条件: 考虑到变体飞行器机翼后掠角λ在整个变形过程中不存在突变,是一个随时间连续变化的过程,整个变形的切换是已知的,即机翼后掠角的变化是事先确定的。因此对于已知的切换序列,当t∈(ti,ti+1),σ(ti)=p,σ(ti+1)=q时,假设存在正定对称矩阵Pp和正常数θp满足: (10) 利用如下的自适应更新律[20]: (11) 式中:q=1,…,p-1,p+1,…,m;泄漏率κp满足 (12) 根据定义1可知,上述切换序列应满足MDDT: (13) 注2考虑到变体飞行器变形过程的实际情况,假设整个切换变形过程是提前已知的。 本文针对带外部干扰的不确定线性切换系统(5),利用自适应更新律(11)和切换控制序列(13),提出了一种新的鲁棒稳定性判据。在切换序列已知的情况下,结合文献[10],给出如下定理。 定理1对于存在外部干扰的不确定线性切换系统(5),当其状态反馈控制器(8)满足自适应更新律(11),且切换序列σ(·)满足MMDT时,该系统是最终一致有界的,且跟踪误差满足: (14) (15) 证明首先,构造Lyapunov函数。 (16) V(ti+1)=eT(ti+1)Pσ(ti+1)e(ti+1)+ 由于 因此,在切换瞬间ti+1处,Lyapunov函数V(t)满足 (17) dT(t)Ppe(t)+eT(t)Ppd(t) (18) dT(t)Ppd(t)≤-θpeT(t)Ppe(t)- eT(t)Ppe(t)+dT(t)Ppd(t) (19) dT(t)Ppd(t)≤-θpV(t)+ (20) 定义正数b为 式中: 下面讨论初始时刻V(t0)≥b和V(t0) 情况1假设当t∈[t0,t0+T1)时,有V(t0)≥b,其中T1为Lyapunov函数到达边界b的时刻。设N1为在[t0,t0+T1)内所有子系统被激活的总次数,N1p为在[t0,t0+T1)内子系统pth被激活的次数。由式(17)和(20)可知,当t∈[t0,t0+T1)时,可得 tN1-2)]V(tN1-2)…≤ tN1-2)]V(tN1-2)…μσ(t0)exp[-ξθσ(t0)(t1- (21) 情况2(V(t0) 证毕 根据定理1,设计并验证“火蜂”变体飞行器的控制器。考虑“火蜂”变体飞行器不同机翼后掠角(15°,30°,45°,60°)对应的纵向短周期线性模型。 其次,设计鲁棒自适应更新律。令θ1=1.8,θ2=1,θ3=0.5,θ4=0.05,解不等式(10),可得到正定对称矩阵Pp,∀p∈Ω,有 考虑“火蜂”变体飞行器的整个变形过程,其切换序列如图2所示,由图2可知,该切换序列包含了变体飞行器由“巡航状态”(λ=15°)到“高速状态”(λ=60°)的整个过程,即能够完整的反映机翼后掠角由“小”变“大”的完整过程。 表1 自适应切换控制器主要参数Table 1 Main parameters of adaptiveswitching controller 图2 变体飞行器切换律Fig.2 Switching law of morphing aircraft Q1=[-45.486 1 -17.900 6] Q2=[-39.768 5 -15.658 7] Q3=[-33.851 4 -13.352 7] Q4=[-26.925 8 -10.707 5] 进行仿真验证,变体飞行器迎角α和俯仰角速率q的时间响应曲线如图3所示。观察可知,在变体飞行器的整个切换变形过程中,2种方法都能够保证飞行器的迎角α和俯仰角速率q快速有效的跟踪参考模型,且在外部干扰的情况下能够保持系统稳定,但是对比发现,本文方法具有更好的抗干扰能力。图4为系统状态跟踪误差的时间响应曲。由图可知:跟踪误差e(t)能够在有效时间内快速收敛,实现系统对参考模型的有效跟踪,在存在外部干扰的情况下,跟踪误差仍能够保持良好收敛性,且在整个变体飞行器变形过程中,本文方法具有良好的抗干扰能力,系统状态的跟踪误差明显小于文献[16]方法。通过上述仿真对比验证可知,利用上文设计的鲁棒自适应切换控制器,在保证变体飞行器在整个切换过程精确稳定跟踪参考模型的同时,具有较好的抗干扰能力。 图3 迎角和俯仰角速率时间响应曲线Fig.3 Time response curves of angle of attack and pitch rate 图4 系统状态跟踪误差Fig.4 System state tracking error 本文针对一类机翼后掠角可变的变体飞行器控制系统设计问题进行了研究。 1) 将变体飞行器的变形过程建模为一类不确定线性切换系统,降低了系统的复杂性,简化了飞行控制系统的设计过程。 2) 设计了一种改进的自适应更新律,消除了系统外部干扰和各类不确定性影响,保证了系统跟踪误差收敛。 3) 考虑到变体飞行器的变形序列提前已知的特点,设计了一种改进的MDDT的切换方法,允许更为快速的切换,降低了本文方法的保守性。 4) 仿真结果证明了所设计的鲁棒自适应切换控制器能够保证变体飞行器在切换过程中精确跟踪参考模型,并具有良好的抗干扰能力。

2 问题描述
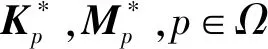

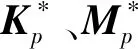

3 自适应切换控制器设计
3.1 自适应更新律设计
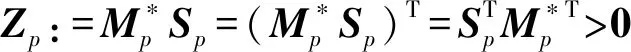

3.2 切换控制律设计

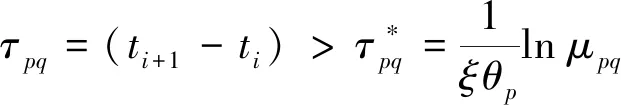
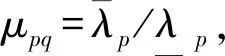
3.3 系统稳定性分析
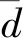
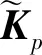
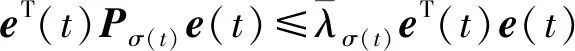
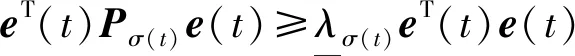
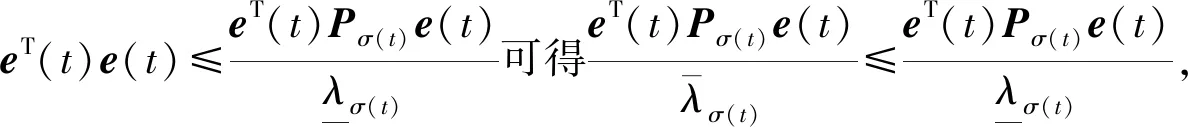
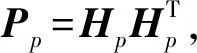

4 仿真验证


5 结 论
