基于BP 神经网络的路面不平度识别
2019-04-07谷盛丰郑玲玲
谷盛丰,顾 久,郑玲玲,赵 旗,李 杰
(1.吉林大学 汽车仿真与控制国家重点实验室,长春 130025; 2.一汽-大众汽车有限公司,长春 130011)
路面不平度是车辆行驶的主要激励,既对车辆平顺性和乘员舒适性有直接影响,也对道路的质量和使用寿命有很大影响。
为了更好地使用车辆,保障道路交通安全,早期都是通过测量来获得路面不平度[1-3]。测量可以获得较为准确的路面不平度,但是需要特定的测量仪器,成本较高,有些测量仪器的测量效率较低,有些测量方法的实现较为复杂。
2007 年以来,国内外学者开始应用神经网络识别路面不平度[3-6]。通过神经网络建立车辆响应和路面不平度之间的关系,既省去人为标定的工作,也省去推导车辆响应和路面不平度之间逆模型的工作,只要具有车辆响应和路面不平度就可以通过训练建立两者之间的关系。训练完成之后,由车辆响应就可以识别路面不平度。
1986 年,Rumelhart 和McClelland 建 立 了BP神经网络,其将误差逆传播算法作为反向计算引入以往正向计算的多层前馈网络,具有完整的数学推导。至今为止,BP 神经网络是应用最为广泛的神经网络[7]。
2008 年, Ngwangwa 等[8]将1/4 汽车平顺性2 自由度模型仿真得到的车身位移作为BP 神经网络的输入,实现了对路面不平度的识别。2010 年, Yousefzadeh 等[9]通过平顺性空间7 自由度模型仿真得到4 个车轮的垂直加速度、车身俯仰角加速度、侧倾角加速度和车身垂直加速度,作为BP 神经网络的输入,对路面不平度进行了识别。2014 年,崔丹丹等[10]建立了平顺性平面4 自由度模型,以车身俯仰角加速度功率谱密度和车身垂直加速度功率谱密度作为BP 神经网络输入,对路面不平度功率谱密度进行了识别。2014 和2015 年,谷正气等[11]和朱一帆等[12]建立了自卸车平顺性空间14 自由度模型,引入遗传算法对BP 神经网络的权值和阈值进行优化以提高收敛精度,将座椅加速度作为BP神经网络输入,对矿山路面不平度进行了识别。
上述基于BP神经网络识别路面不平度的研究,既没有对识别效果进行定量分析,也没有研究不同车辆响应组合对路面不平度识别效果的影响。
为此,针对上述问题,本文引入神经网络识别效果的评价指标,建立前后轮路面不平度和汽车平顺性模型,通过仿真获得车辆响应和路面不平度,构造不同的车辆响应输入方案,采用BP 神经网络对前后轮路面不平度进行识别,确定最优输入方案,为实际应用提供理论和方法基础。
1 BP 神经网络基本原理和评价指标
1.1 BP 神经网络基本原理
BP 神经网络由输入层、输出层和隐含层组成,每层包含若干个神经元节点。输入层负责将输入数据集中起来,对输入数据进行权值和阈值的运算,再将运算结果传递给隐含层。隐含层可以是一层也可以是多层,负责接收数据,继续进行权值和阈值的运算,最终传递给输出层。输出层负责将传递过来的数据和期望输出进行比较,得到误差值,再反向修正权值和阈值[1-3]。
输入层神经元节点数为n、隐含层为1 和隐含层神经元节点数为l、输出层神经元节点数为m的BP 神经网络,如图1 所示。其中,为输入数据;yk,k=1, 2,… ,m为输出数据;ok为期望输出数据;ek为期望输出数据与输出数据之间的误差;ωij和ωjk分别为输入层与隐含层的权值和隐含层与输出层的权值;aj为隐含层阈值;f为隐含层传递函数;bk为输出层阈值;g为输出层传递函数。

图1 BP 神经网络结构
确定BP 神经网络结构后,要对BP 神经网络进行训练,训练过程如下。
第1 步:网络初始化
确定输入层神经元节点数n,输出层神经元节点数m,隐含层层数p与隐含层神经元节点数l;初始化输入层与隐含层之间的权值ωij,隐含层与输出层之间的权值ωjk,隐含层阈值aj,输出层阈值bk;设置训练步数,学习率η,隐含层和输出层的传递函数f和g。
第2 步:隐含层输出计算

第3 步:输出层输出计算

第4 步:误差计算

第5 步:权值更新
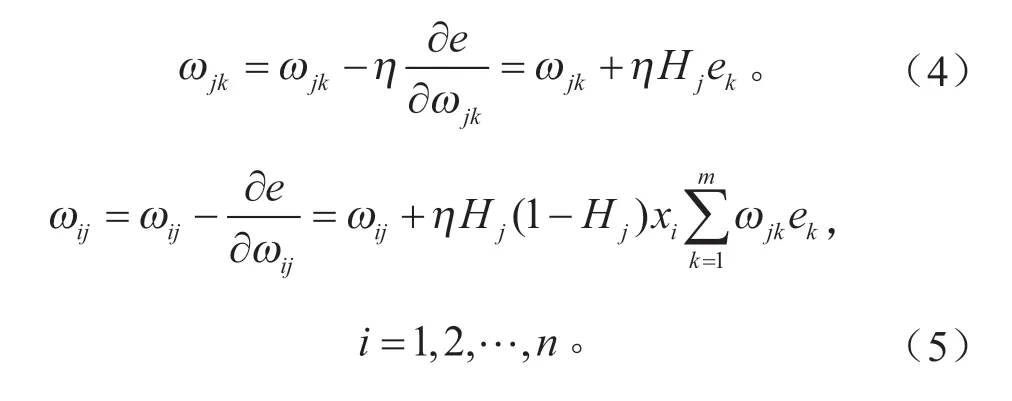
第6 步:阈值更新

第7 步:判断训练是否结束,如果没有结束,则返回步骤2。
上述权值和阈值的更新的公式,仅是一种表示方法,根据训练算法其可能会有所不同。
1.2 评价指标
为了对神经网络识别结果进行评价,引入相关系数和均方根误差两个评价指标[13-14]。
(1)相关系数(R)
相关系数表示输出数据和期望输出数据变化趋势一致的程度,相关系数越高,说明识别得越好。
相关系数的公式为:

式中:yi和ai分别为输出数据和期望输出数据的第i个点和别为输出数据和期望输出数据的平均值;n为采样点数。
(2)均方根误差(RMSE)
神经网络在训练或测试过程中,会因为自身的因素产生一定的随机误差,均方根误差也称为标准误差,是表示随机误差的一种最基本的方式,可以反映路面不平度识别结果的稳定性。均方根误差越小,识别结果越好,越稳定可靠。
均方根误差的公式为:

2 路面不平度和平顺性的模型
2.1 前后轮路面不平度的滤波白噪声模型
采用滤波白噪声模型描述前轮路面不平度 ,表示为[15]:

根据前后轮路面不平度q1(t)和q3(t)的相关性,后轮路面不平度q3为[15]:
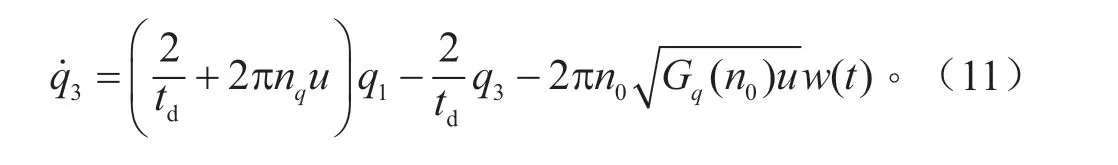
式中:td为前后轮滞后时间。
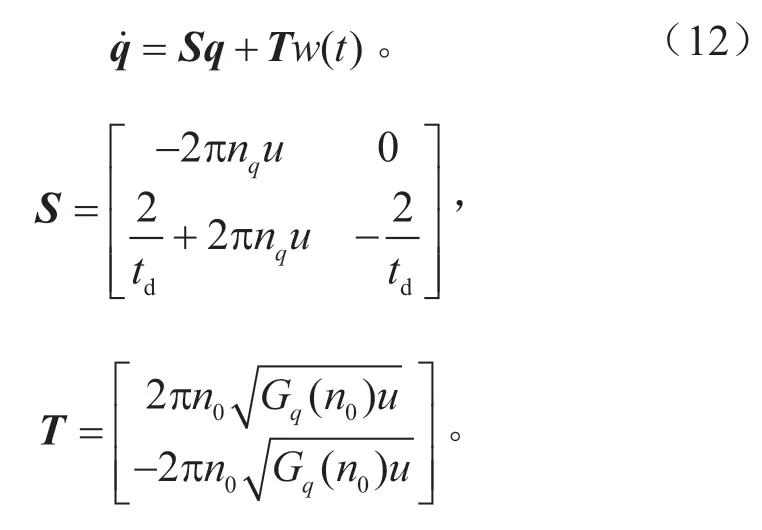
2.2 汽车平顺性4 自由度平面模型
平顺性4 自由度平面模型,由车身、前后悬架和前后车轮组成,如图2 所示。该模型的参数为:车身质量mb,车身绕其质心的转动惯量Iy,前轮质量m1,后轮质量m3;前悬架垂直阻尼c1,后悬架垂直阻尼c2;前悬架垂直刚度k1,后悬架垂直刚度k3,前轮胎垂直刚度kt1,后轮胎垂直刚度kt3;车身质心到前轴的纵向距离a,车身质心到后轴的纵向距离b;车身质心垂直位移zb,车身俯仰角位移θ,前轮垂直位移z1,后轮垂直位移z3,前车身垂直位移zb1,后车身垂直位移zb3,前轮路面不平度q1,后轮路面不平度q3。

图2 平顺性4 自由度平面模型
应用拉格朗日方法,可以得到平顺性4 自由度平面模型[16],即:

引入x=[ ]T
z z,˙ ,将式(13)转化为状态空间方程,有:

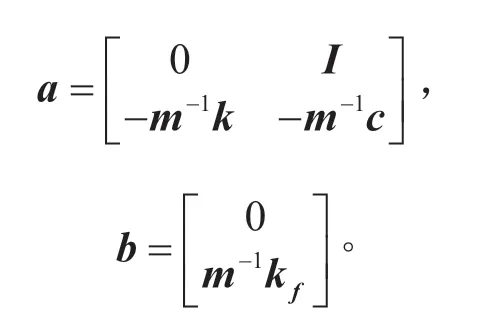
取新变量y=[q,x]T,联立式(12)和式(15),得:

对于平顺性4 自由度平面模型,前悬架动挠度fd1和后悬架动挠度fd3表示为:

3 路面不平度的BP 神经网络识别
3.1 BP 神经网络输入和输出的仿真获得
为了说明应用BP 神经网络识别路面不平度的原理,本文通过平顺性4 自由度平面模型仿真获得前后轮路面不平度和车辆响应:各个质量的位移、速度和加速度以及前后悬架动挠度。
采用某汽车参数,取常用路面等级B 级,车速为常用车速60 km/h,仿真时间为20 s,采样点为0.01 s,通过对式(16)进行仿真,得到的路面不平度和车辆响应,每个量为2 000 个点。
进行BP 神经网络训练时,将车辆响应和路面不平度的前1 500 个点作为输入和输出,构成训练集样本。
将车辆响应的后500 个点作为测试集样本的输入,将其代入训练好的BP 神经网络,获得路面不平度,与路面不平度的后500 个点进行比较,确定BP 神经网络应用的效果。
3.2 BP 神经网络结构设计
参考BP 神经网络应用的案例,将BP 神经网络分为3 层结构,输入层、输出层和隐含层各占1 层。
输入层神经元个数n由后续的输入方案确定,输出层神经元节点数m取为2,代表前后轮路面不平度,隐含层神经元节点数l为[7]:

式中:a为0 ~10 之间的常数。
隐含层传递函数f取为logsig,输出层传递函数g取为purelin,分别表示为:
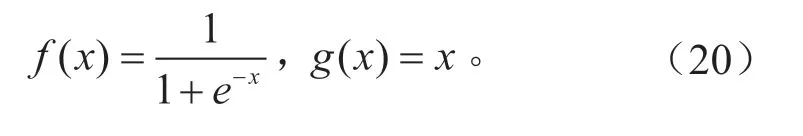
神经网络的权值和阈值通过训练算法调整,BP神经网络有13 种训练算法。经反复试验,最终选取trainlm,该算法训练速度快,识别精度高[7]。
3.3 输入方案确定
输入方案确定是指选择哪些车辆响应作为神经网络的输入。以往基于神经网络识别路面不平度的研究,不同学者选择了不同的车辆响应作为神经网络的输入[8-12]。
为了更好地发挥BP 神经网络识别路面不平度的作用,本文采用40 种输入方案,车辆响应的组合见表1。

表1 40 种输入方案
将上述40 种输入方案确定的车辆响应作为BP神经网络的输入,对前后轮路面不平度进行识别,评价指标见表2。

表2 各种方案的评价指标

续表2
由表2 可知,前后轮路面不平度识别结果较好的8 种方案是26、27、29、36、37、39 和40。其中,方案36、37、39 和40 的相关系数较高,均方根误差也较小,这是因为这4 种方案输入车辆响应个数较多,基本包含了所有与路面不平度相关的车辆响应。显然,方案40 是最为理想的输入方案。但是,如果将方案40 应用在实车上就有些不现实,不可能都通过实车测试得到所有这些车辆响应,因此,需要找出最关键的车辆响应。
进一步分析8 种较好方案发现,它们均包含z1和z3。因此,z1和z3是识别前后路面不平度的两个关键车辆响应,即车轮响应是准确识别路面不平度的关键。
为了进一步分析车轮与路面不平度相关的车辆响应,由式(13)得到前后车轮的振动方程:

对式(20)和式(21)进行变化,有:

由式(22)和式(23)可知,与前轮路面不平度密切相关的车辆响应是:前车轮垂直加速度前车轮垂直位移前悬架动挠度和前悬架动挠度导数与后车轮路面不平度密切相关的车辆响应是:后车轮垂直加速度后车轮垂直位移z3、后悬架动挠度和后悬架动挠度导数
由上述分析,可以得到4 种附加输入方案,见表3。
由这4 种输入方案,再对路面不平度进行识别,评价指标见表4。

表3 四种附加输入方案
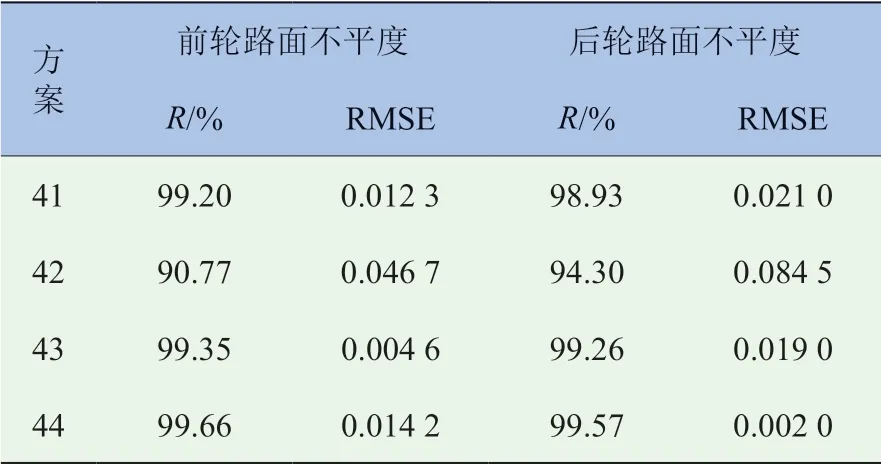
表4 四种附加输入方案的评价指标
由表4 可知,4 种输入方案的识别结果较好的是方案41、43 和44,这些识别较好的方案均包含对应的车轮垂直位移。这是因为,由式(23)和式(24)可知,现有车辆前后轮胎刚度比其它参数大很多,其它几项与z1和z3相比要小很多,所以z1和z3在路面不平度中占有很大一部分,这也是之前40 种方案中,缺少z1和z3的输入方案识别结果不太理想的原因。但是,在方案29 中,车辆响应仅有z1和z3,其与方案41、43 和45 相比还有一定差距,这说明式(23)和式(24)后面的项对路面不平度也有影响。最终,综合考虑识别指标的精度和输入车辆响应的个数,选择方案43 为最优方案。
3.4 最优方案的识别结果
采用方案43 的车辆响应作为输入,进行路面不平度识别,识别的前后轮路面不平度,如图3所示。

图3 前后轮路面不平度预测值与期望值的对比
由图3 可知,识别的前后轮路面不平度(预测输出)与理想的路面不平度(期望输出)吻合得很好,说明最优输入方案的选取是合理的,应用BP 神经网络可以较好地识别出路面不平度。
4 结论
为了更好地应用BP神经网络识别路面不平度,总结了BP 神经网络的基本原理,引入相关系数和均方根误差作为识别评价指标。建立了前后轮路面不平度滤波白噪声模型和汽车平顺性4 自由度平面模型,通过仿真得到前后轮路面不平度和车辆响应。
进行了BP 神经网络结构设计,先后构造了44种车辆响应输入方案,采用3 层BP 神经网络识别前后轮路面不平度,通过评价指标选出最优输入方案,分析了最优输入方案的识别效果,为后续实际应用BP 神经网络识别路面不平度奠定了一定的前期工作基础。
