AGC环路设计的Matlab-Simulink模型建模及验证
2019-04-04井永成尹军舰李仲茂唐舸宇冷永清
井永成 尹军舰 李仲茂 唐舸宇 冷永清
关键词: 自动增益控制; Matlab?Simulink模型; 环路设计; 高动态; 时域模型; 功率域模型
中图分类号: TN108+.4?34 文献标识码: A 文章编号: 1004?373X(2019)06?0083?05
Abstract: A complete automatic gain control (AGC) loop model based on the Matlab?Simulink is constructed and verified. The model can analyze the AGC control process from two respects of time amplitude and power amplitude, and well display and predict the loop feature, so as to conveniently evaluate whether the AGC loop can meet the requirements of the system. With the assist of the model, a high dynamic AGC loop with its input dynamic range of –72~–12 dBm and output dynamic range of –19.7~–19.2 dBm is implemented, taking the variable gain amplifier, radio detector, analog?to?digital converter, digital?to?analog converter and field programmable gate array (FPGA) as core devices. The output power difference of the loop simulation and actual test is less than 1.3 dB, and the control time processes are consistent, which indicates that the simulation results of the AGC loop are basically consistent with its actual test results.
Keywords: automatic gain control; Matlab?Simulink model; loop design; high dynamic; time?domain model; power?domain model
0 引 言
随着接收机与信源间距离远近的变化,天线端接收到的信号功率具有很大的波动[1?2]。为使基带能够正确解调信号,接收机前端需根据输入信号的强度自动调整其增益,从而得到电平相对稳定的输出信号,这项功能是由系统中的自动增益控制(Automatic Gain Control,AGC)环路实现的。
在AGC环路中,环路结构和算法是影响AGC环路性能的重要因素,因此如何保证算法和环路结构的有机统一,是实现高性能AGC的难点。针对以上问题,相关文献利用Matlab?Simulink建模仿真的方式来搭建电路结构,验证算法的合理性,进而评估整个通信系统乃至AGC环路的性能[3?5]。该方法可以从原理上对算法进行验证,且算法的修改灵活、简便。然而之前的工作仅涉及算法仿真,没有在实际电路调试中体现出应用价值。本文基于Matlab?Simulink建立一种新的AGC模型,该模型从理论上分析AGC环路的性能,提取关键参数,并将该关键参数应用于实际电路调试,极大地缩短了调试周期。
1 构建AGC环路
AGC环路可由模拟器件构成,也可由数字、模拟器件混合构成,本文分析的数/模混合构建的AGC环路,由检波器、可变增益放大器(Variable Gain Amplifier,VGA)和ADC,DAC等电路元件构成。如图1所示,输入信号经过两级相同的VGA放大后,通过耦合器向检波器馈入适当电平的信号,检波器的输出电压VDET由ADC转换为数字量,再由AGC算法单元进行数据处理,处理结果决定DAC的输出电压,从而控制VGA的增益。其中:IFin为输入信号;IFout为输出信号;VG为VGA的控制电压;VDET为检波器输出电压。

2 AGC環路模型
随着电路结构的确定,电路中各个元件的选择,以及元件与AGC算法的匹配问题成为能否实现AGC环路的关键。所以,需要对各个元件的通用模型建模,模拟实际电路,以降低实际电路的研发成本,提高效率。
基于AGC环路结构和各部分的特性构建了图2所示的AGC时域模型,其中模块1~模块4分别为AGC输入信号发生器、可变增益放大器模型、功率检测器的模型以及AGC的算法模型。工作原理如下:通过AGC输入信号发生器生成脉冲型的包络信号,该信号经可变放大器增益模型VGA1和VGA2放大后,由功率检波器模块检测被放大后的信号功率,并将检测值送入AGC算法模块进行数据处理,根据处理结果决定VGA1和VGA2的控制电压,进而控制增益,达到调整信号幅度的目的。
输入信号发生器利用不同幅度的正弦波与不同相位的方波做点乘、叠加运算可模拟周期性变化的功率信号,用作AGC系统的激励。
可变增益放大器的增益和控制电压的关系有对数型、线性型、指数型等,但对数型具有更宽的增益范围[9?10],更符合实际系统需求,所以本文选用对数型进行建模。

功率检测器的模型如图4所示,输入信号经过限幅器1做半波整流得到正弦波的正半周期,在经低通滤波器得到其直流分量,该直流分量代表了输入正弦波的幅度,又通过转换公式模块将电压幅度值转换为功率值,最后根据所采用的检波器模型插入检波公式得到检波电压值。由于检波器输出电压的区间受到供电电压与器件特性的限制,因此最后经过限幅器2限制合理的输出电压范围,得到最终的输出VDET。

根据不同检波器特性可知,均方根检波器可以用于各种波形的信号功率检测。检波公式的输出电压VDET与被检测功率Pout在正常工作区域符合式(2)的线性关系。

3 结果与分析
为了测试AGC模型的实际应用效果,经过研究,选择相应的VGA器件[6]和功率检波器[7]并搭建电路进行验证。根据所选器件特性可知,式(1)和式(2)中,k取50,b取-5,k1取0.05,b1取2.65。目标功率Paim选定为-20.5 dBm。
AGC控制过程的时域模型仿真及实测结果如图5、图6所示。

从图5可以观察到,输入信号为周期性的脉冲型的包络信号,输出信号为有周期性的窄脉冲凸起的包络信号,VGA的控制电压波形也呈周期性变化,且变化周期和输入信号的周期相同,但变化趋势和输入信号恰好相反。随着输入信号的幅度由大变小,检波电压VDET呈现一个负向的不规则的窄脉冲;随着输入信号的幅度由小变大,检波电压VDET呈现一个正向的不规则的窄脉冲,输出信号呈现窄脉冲包络信号;其余时间、检波电压VDET和输出信号均保持一个恒定值。该正负脉冲的宽度近似等同于椭圆形标注所显示的VGA1和VGA2之间的调整时延,也近似等同于输出信号的窄脉冲宽度。这是因为AGC环路存在响应时间,即从检波器检测到输入信号变化到VGA的控制电压做出调整所需的时间。这期间VGA的增益保持不变,输入信号的波动呈现在输出信号和检波电压的波形之上。
从图6可以观察到,中频输入信号为周期性的脉冲信号,该输入信号由矢量信号发生器产生,其功率以800 μs为周期变化,其中400 μs功率为-10 dBm,另外400 μs功率为0。中频输出信号有周期性的窄脉冲凸起,VGA的控制电压VG和输入信号的周期相同,但是变化趋势相反。检波器的检波电压VDET的变化趋势基本和图5中检波电压波形一致,但是在功率为0的时间段内,VDET快速下降至一个较低的电平,随后随着VG的升高而渐渐升高。这是因为所使用的检波器AD8362为均方根检波器[7],其检测功率为工作频带内积分总功率而非峰值功率。在目标频率两侧,噪声也被VGA放大而具有一定功率,因此即使输入信号为零,检波器仍能检测到一个非零的积分噪声功率,且该功率随VGA增益的增加而增大。因此,图6中输入功率由高变低时,控制电压与检波电压出现了较缓慢的非理想上升过程。除此之外,两图所呈现的AGC行为基本一致,仿真和实测结果吻合。
AGC的功率域模型的仿真结果与实测结果如图7、图8所示。
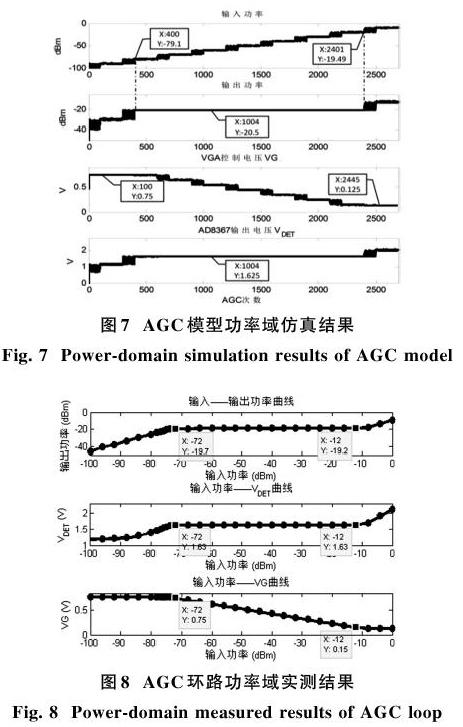
从图7可以观察到,输入信号的功率范围为-100~0 dBm。当输入信号的功率范围为-79.1 ~-19.49 dBm时,输出信号的功率被稳定地控制在
-20.5 dBm,与所设定的目标功率值相同。当输入信号的功率范围为-100~-79.1 dBm时,VGA的控制电压保持最大值,可变增益放大器保持最大增益,所以输出信号的功率随输入信號功率的增大而增大。当输入信号的功率范围为-19.49~0 dBm时,VGA的控制电压保持最小值,可变增益放大器保持最小增益,输出信号的功率也随输入信号功率的增大而增大。在输入信号很弱或很强这两种情况下,输入信号强度超出了AGC可调整的范围。根据以上的分析,通过仿真结果,该模型可以预测实际AGC电路中调整范围的大小和调整特性。
从图8可以观察到,输入信号的功率范围为-100~0 dBm。当输入信号的功率范围为-72~-12 dBm时,输出信号的功率被稳定地控制在-19.7~-19.2 dBm之间。当输入信号的功率范围为-100~-72 dBm时,VGA的控制电压保持最大值,可变增益放大器保持最大增益,所以输出信号的功率随输入信号功率的增大而增大。当输入信号的功率范围为-12~0 dBm时,VGA的控制电压保持最小值,可变增益放大器保持最小增益,输出信号的功率也随输入信号功率的增大而增大。在输入信号很弱或很强两种情况下,输入信号强度超出了AGC可调整的范围。
通過与图7对比,AGC环路实际可控输入范围为-72~-12 dBm,这与模型预测的-79.1~-19.49 dBm具有约7 dB的平移关系,这是噪声与检波器的均方根特性等非理想因素导致的。另外,因滤波器等无源器件参数的改变导致通道固定衰减及耦合系数发生变化,实际的AGC电路输出功率范围为-19.7~-19.2 dBm,和模型预测20.5 dBm相比,最大误差为1.3 dB;除此之外,两图呈现的AGC行为基本一致,实测结果很好地印证了仿真结果。
4 结 论
本文提出一种基于Matlab?Simulink的新高动态AGC环路模型。该模型从时域和功率的角度,分析了AGC环路的动态特性。在该模型的辅助下,实现了一种输入功率为-72~-12 dBm,输出功率为-19.7~
-19.2 dBm的高动态AGC电路。该AGC环路的实测结果与仿真结果基本吻合,表明该模型具有良好的预测与分析特性。
参考文献
[1] SONG Y, YU X, JIN Z, et al. A 49?dB DR wide locking range hybrid AGC for an ISM?band receiver in 0.18 μm CMOS [C]// Proceedings of IEEE International Symposium on Radio?Frequency Integration Technology. Hefei: IEEE, 2014: 1?3.
[2] 池保勇,余志平,石秉学.CMOS射频集成电路分析与设计[M].北京:清华大学出版社,2006.
CHI Baoyong, YU Zhiping, SHI Bingxue. Analysis and design of CMOS RF integated circuits [M]. Beijing: Tsinghua University Press, 2006.
[3] 尹立贤.基于Simulink模拟与数字通信系统建模研究[J].信息化建设,2016(5):66.
YIN Lixian. Modeling of analog and digital communication system based on Simulink [J]. Informatization construction, 2016(5): 66.
[4] 高颖,冯浩,张顺,等.基于Simulink的模拟与数字通信系统建模与仿真[J].现代电子技术,2013,36(7):64?67.
GAO Ying, FENG Hao, ZHANG Shun, et al. Modeling and simulation of analog and digital communication systems based on Simulink [J]. Modern electronics technique, 2013, 36(7): 64?67.
[5] 陈永森,吴海.基于Simulink的数字AGC系统设计与仿真[J].舰船电子对抗,2010,33(5):88?91.
CHEN Yongsen, WU Hai. Design and simulation of digital AGC system based on Simulink [J]. Shipboard electronic countermeasure, 2010, 33(5): 88?91.
[6] Analog Devices Inc. AD8367: 500MHz, linear?in?dB VGA with AGC detector (Rev. A) [EB/OL]. [2005?07?05]. http://www.analog.com/media/en/technical?documentation/evaluation?documentation/AD8367.pdf.
[7] Analog Devices Inc. AD8362: 50 Hz to 3.8 GHz 65 dB TruPwr? detector (Rev. F) [EB/OL]. [2016?09?15]. https://www.analog.com/media/en/technical?documentation/data?sheets/AD8362.pdf.
[8] 樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2016.
FAN Changxin, CAO Lina. Principles of communications [M]. Beijing: National Defense Industry Press, 2016.
[9] 苏明.短波接收机前端大范围AGC控制电路的研制[D].武汉:武汉理工大学,2012.
SU Ming. The design of the large range AGC control circuit in the front?end of short?wave receiver [D]. Wuhan: Wuhan University of Technology, 2012.
[10] KHOURY J M. On the design of constant settling time AGC circuits [J]. IEEE transactions on circuits and systems II: analog & digital signal processing, 1998, 45(3): 283?294.
