基于ARCH族模型的可转换债券收益率杠杆效应研究
2019-04-04刘润东闫振坤青岛大学经济学院山东青岛266000
刘润东,闫振坤 (青岛大学经济学院,山东青岛266000)
一、引言
对于投资者而言,可转债具有股票和债券的双重特性,收益率相对于股票期货而言比较平稳,是较为稳健的投资品种。对于上市公司而言,它是一种非常灵活的优秀融资工具,相比定向增发具有发行条款灵活等优点,偏股型的可转债可以延迟股本的稀释,而偏债型的可转债能够使融资成本大幅降低。对于证券监管部门而言,发行可转债需要满足更多财务与金额方面的规定与条件,便于证监会监管。我国可转债市场相较于欧美等资本市场开展时间较晚,然而无论从规模还是从法律规定的完善来看进展较为快速。图1是2003-2017年可转换债券的发行规模与数量,从图1可以看出可转换债券的发行规模与数量受股市波动与政策的影响较为严重,2017年可转债的发行规模与数量达到顶峰。
波动率中的杠杆效应意味着波动率对价格的上涨和下跌的反应不同,即波动率反映价格下跌给财产持有人带来的损失大于价格上涨给其带来的收益。价格下降时收益率的降幅要大于价格上升时收益率的涨幅,表示为一种非对称效应。[1]杠杆效应与投资者的心态有关,反映在股市中即为追涨杀跌。
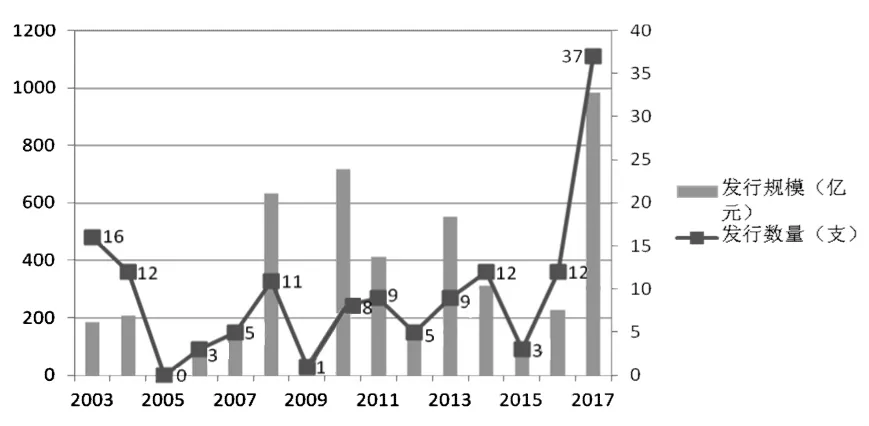
图1 2003-2017年可转债发行规模与数量
二、文献综述
学者们对于可转换债券的研究主要集中在其价格方面以及发行可转债行为方面。赵静、姜伟、杨春鹏[2]等从可转债持有人情绪角度进行定价分析,获得了情绪系数对可转债价格的影响规律。秦学志、胡友群、石玉山[3]将可转债回售条款纳入定价考虑范围内,并实证分析其合理之处。而牟晖、韩立岩、谢朵等[4]通过对发行可转债的实证研究,发现可转债发行公告对股票价值存在着明显的负效应。张秀艳、张敏[5]使用二元GARCH模型对可转债市场与股票市场进行分析,发现债市与股市之间的收益率条件波动之间具有正相关性。孙晓晓[6]运用ARCH族模型和误差修正模型等多种方法对上证可转债指数进行分析,发现股票市场与可转债市场的对数收益率具有单向波动溢出效应。罗美娟、吴优[7]对上市公司发行可转换债券公告期的股票收益率进行了统计,发现公告对于可转债正股具有正效应,但是持续时间较短,仅仅维持在公告日之内。程大涛[8]通过对我国发行可转债的上市公司进行实证分析,发现可转债的发行行为对于上市公司具有不良影响,应该对投资人的利益更为关注。
通过文献综述,可发现对于可转债的研究主要集中在可转债的定价领域与可转债与其他市场的相关性分析。本文从可转债的波动率出发,通过建立的Arch族模型的系数研究可转债是否具有杠杆效应,并寻求能反应可转债指数收益率的最佳模型。
三、模型介绍
(一)GARCH 模型
为了简化ARCH模型,Bollerslev[9]提出了广义ARCH模型,又称为GARCH模型。对于一个对数收益率序列rt,令αt=rt-ut为t时刻的信息,若αt满足下式,则称αt服从 GARCH(p,q)模型。

其中,εt是独立同分布随机变量序列,且其均值是0方差为1。
(二)求和GARCH模型
若GARCH方程中AR多项式有一个单位根,则可建立一个求和广义自回归条件异方差模型。与ARIMA模型相似的是,IGARCH模型的主要特点是以前的平方扰动 ηt-i=α2t-i-σ2t-i(i>0)对于 α2t具有长久影响,IGARCH(1,1)模型可以写成如下形式:
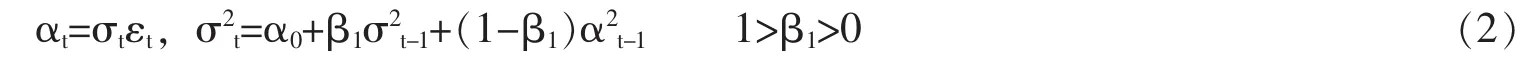
(三)GARCH-M 模型
在金融界,资产的收益率可能依赖于其波动率,Engle、Lilien、Robins认为序列的波动影响其均值并由此构造GARCH-M模型,其中 “M”体现收益率的条件均值GARCH。GARCH-M模型的构造体现了序列均值和条件方差之间具有某种相关关系,将条件标准差看作附加回归因子建模,简单的GARCH(1,1)-M模型可写成:
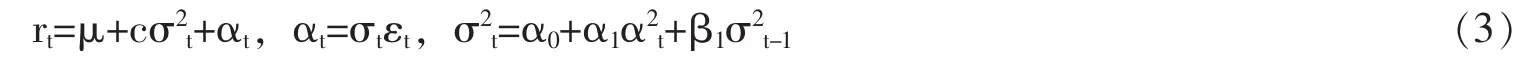
其中,μ与c均为常数。参数被认为是风险溢价参数。c的正值意味着金融资产的收益率与其以前的波动率正相关。文献中还出现过其他一些具体的风险溢价的形式,如 rt=μ+cσt+αt和 rt=μ+cIn(σ2t)+αt。
(四)指数GARCH模型
金融数据往往具有杠杆效应,为在模型中克服杠杆效应,Nelson构建了指数GARCH(EGARCH)模型。即为在模型中体现时序波动率的杠杆效应,考虑加权的信息:

其中,θ 和 γ 为实常数。εt和|εt|-E(|εt|)都是零均值的独立同分布且连续的序列。因此,E[g(εt)]=0 重新改写 g(εt)为下面的公式,从公式中可以看出非对称性:

(五)门限GARCH模型
门限GARCH模型 (也称为TGARCH模型)也可以用来体现序列的杠杆效应。TGARCH(m,s)模型的形式为:

其中,αi、γi和βi为非负参数,它们所满足的条件与GARCH模型相同。通过模型可知,正的 αt-i对 σ2t的贡献为 αiα2t-i,而负的 αt-i对 σ2t有更大的贡献(αi+γi)α2t-i,其中,γi>0。该模型使用0作为阈值来区分过去干扰的影响。
其中,Nt-i是关于αt-i是否为负值的指示变量,即:

四、实证分析
(一)样本数据说明
中证转债指数(000832)由70只上市流通的可转债构成,包括目前上市流通的大部分可转债,能够较好地反应可转债市场的状况。本文使用中证转债指数反映可转债市场,以中证转债指数为研究对象,数据选取的时间从2012年9月12日到2018年6月19日,共得到1399个数据。使用收盘的价格cl来计算对数收益率,设对数收益率为rt,计算收益率所使用的公式为rt=lnclt-lnclt-1。本文所使用的数据来自大智慧金融科技终端,并使用R软件进行分析。
(二)拟合AR-GARCH模型
根据图2可知,可转债对数收益率图像围绕在0值附近波动,而且可以看出图像没有明显的趋势,可以认为中证转债指数对数收益率为平稳序列。收益率在2015年波动率较高,而在剩下的时间段波动较低,说明存在波动率聚集的现象。另外,通过时间序列图可以看出波动率对对数收益率的大幅上升和大幅下降的反应大致相同,表明可转债可能不具有杠杆效应这一现象。
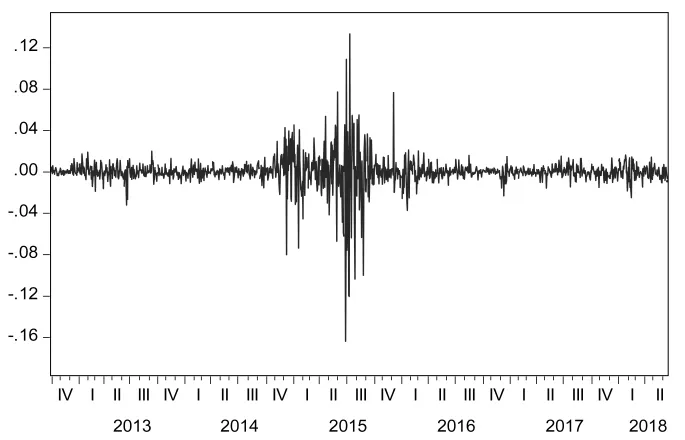
图2 中证转债指数对数收益率时间序列图
仅观察时间序列图判断其平稳性可能并不严谨,可通过ADF检验来验证其平稳性。由ADF检验可知,p值为0.01,在0.05的显著性水平上拒绝原假设,可得出结论:可转债对数收益率具有平稳性,这也与时间序列图中观测所得到的结论相一致。
auto.arima函数可以依照AIC、AICC、BIC的数值判定合适的阶数进而自动拟合模型。通过使用auto.arima函数,得出结论:对数收益率拟合arima(2,0,2)模型较为合适。使用arima函数进行拟合,结果见表1。
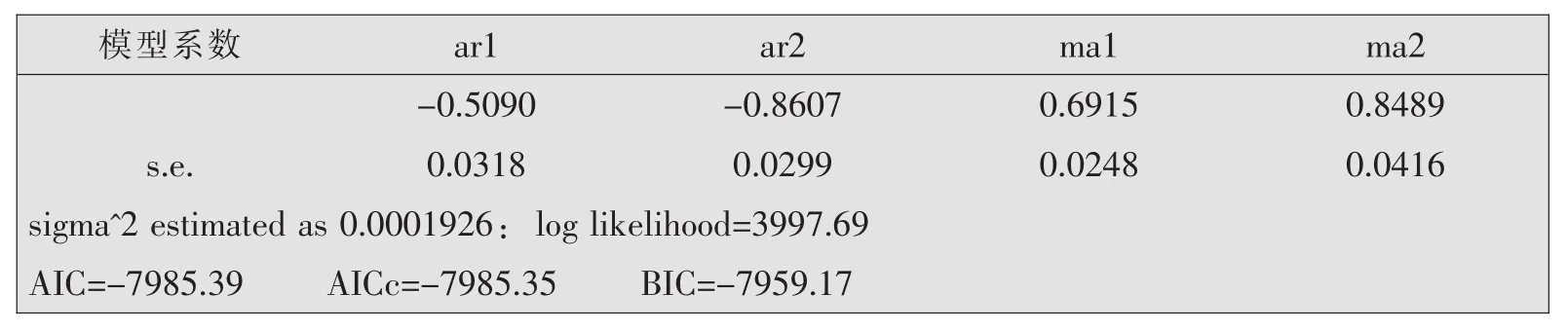
表1 arima模型拟合结果
拟合arima模型后提取残差序列,并绘制残差序列的时序图,得到图3。
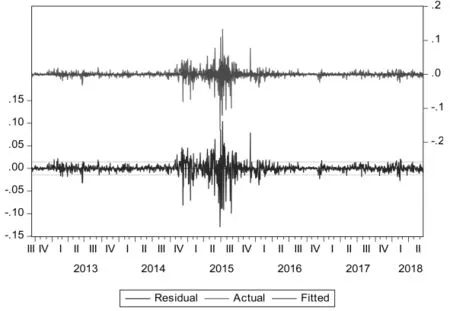
图3 arima(2,0,2)模型的残差时序图
由图3可知,残差在2015年的波动率较高,而在其他时间段内波动率较低,存在着波动率的聚集性,因而可能存在着ARCH效应[11]。ARCH效应可以应用Portmznteau Q检验和LM检验来进行判断。对可转债对数收益率的残差序列{εt}进行Portmznteau Q检验与对其平方序列{ε2t}进行LB检验相同,所以本文对可转债对数收益率的残差平方序列进行LB检验。检验的原假设为H0:残差平方序列纯随机,因为p-value小于0.05,所以拒绝原假设,也就是说残差序列具有ARCH效应,因此可以对残差序列拟合ARCH族模型。
因为残差序列具有ARCH效应,因而可以利用r语言中的garchFit函数拟合AR-GARCH 模型,通过多次运行并选择 arima(1,0,2)+GARCH(1,1)来进行拟合,得到表2所示的结果。
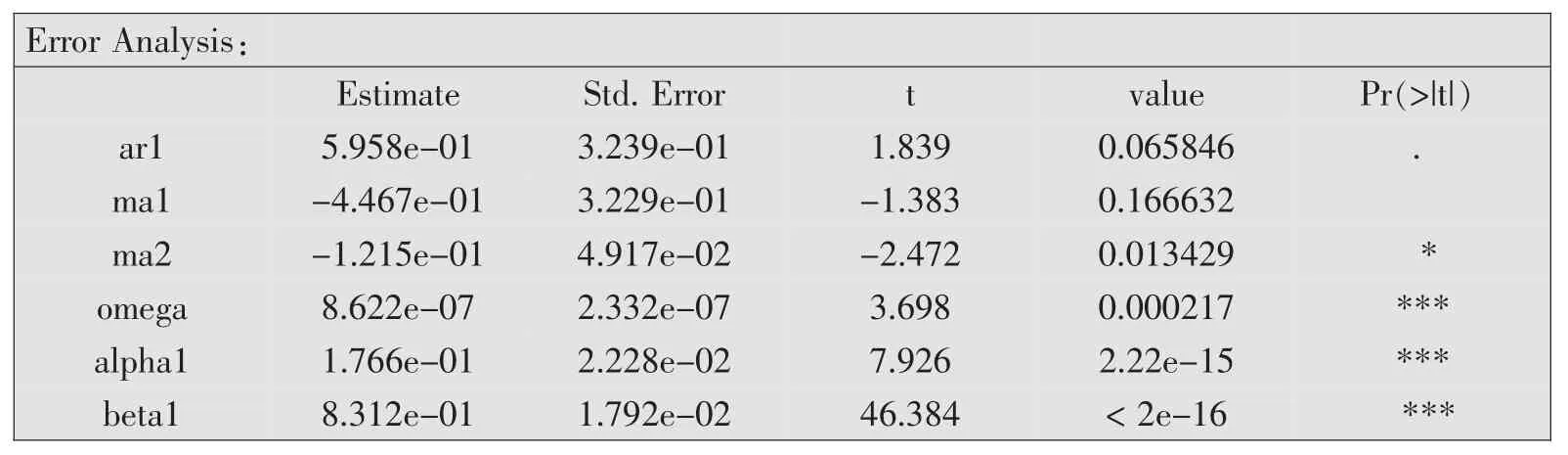
表2 arima(1,0,2)+GARCH(1,1)模型的拟合结果
通过分析可知,arima(1,0,2)+GARCH(1,1)模型的系数除了 ma1 外都通过了检验,表明使用该模型拟合可转债对数收益率比较好。同时,通过表3可得出结论,模型的残差项为正态分布,且没有自相关性和ARCH效应。模型的具体形式见式(8):
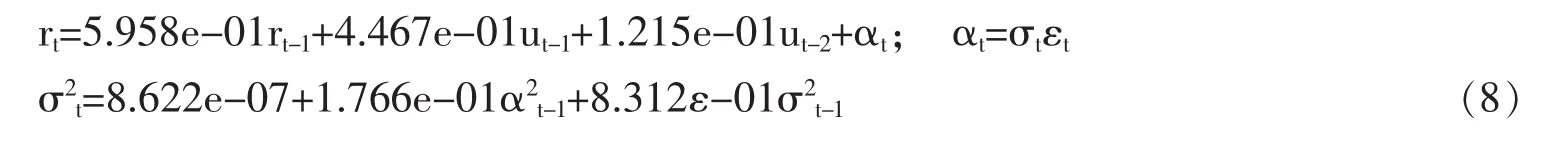
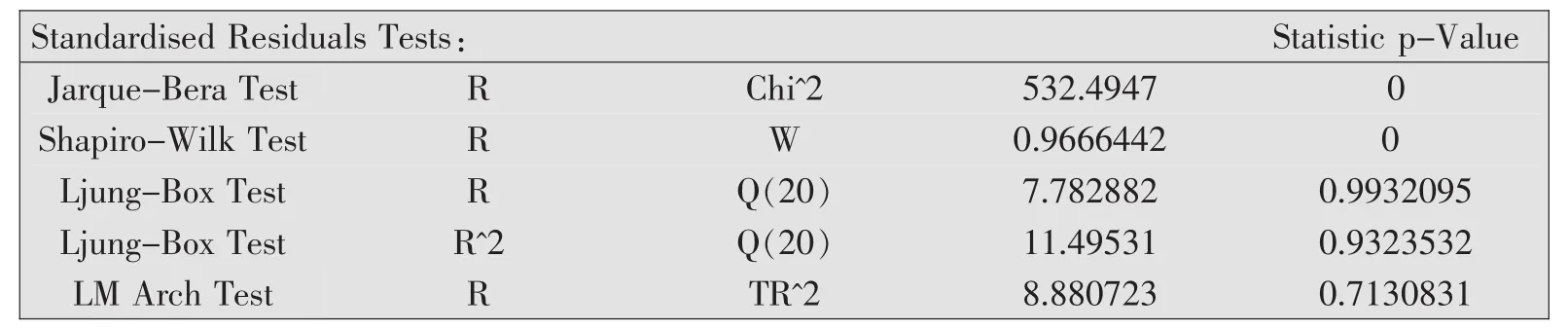
表3 模型残差的检验
(三)拟合GARCH族模型
根据表3可知,LM Arch Test的p值为0.7130831,因而不能拒绝原假设H0:残差的平方序列纯随机,因而可转债具有ARCH效应,因此可以直接对可转债的对数收益率拟合GARCH族模型。通过使用R软件直接对对数收益率进行拟合,并选择其中条件方差系数可得表4。在表4中,mu表示为均值方程中的系数μ,omega、alpha1、beta1分别对应于各GARCH族模型中的 α0、α1、β1,gam1 在 EGARCH 和TGARCH模型中表示λ、在GARCH-M中表示参数c。在EGARCH模型中,通过参数gam1来表示杠杆效应,在实际应用中,gam1为负数时表明具有杠杆效应;TGARCH模型是另一个用来处理杠杆效应的模型,通过观察TGARCH模型可知,正的αt-j对σ2t的贡献为 αiα2t-i,而负的 αt-j对 σ2t有更大的贡献(αi+γi)α2t-i,其中 γi>0[10]。因此当 γi不显著时,表明使用TGARCH模型拟合函数并不合适,可转债的对数收益率不具有杠杆效应。通过对表5分析可知EGARCH模型的gam1大于0且不显著,TGARCH模型的gam1不显著,因此可以确定可转债的对数收益率不具有杠杆效应。
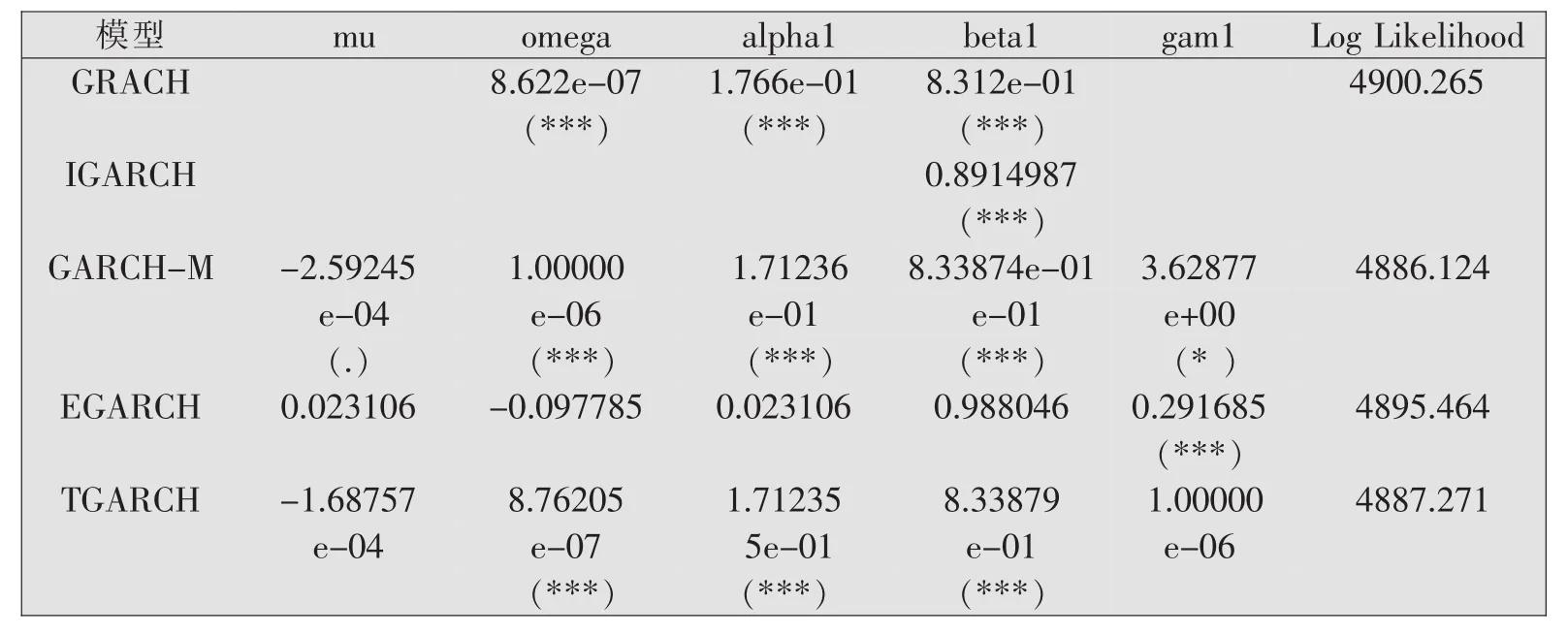
表4 对GARCH族模型条件方差的系数
根据表4可知,AR-GARCH模型与GARCH-M模型之中的参数大部分在0.001置信水平下显著,AR-GARCH模型和GARCH-M模型应用于构造对数收益率时序可能比较合适,而IGARCH模型中只给出了beta1的参数,因此使用IGARCH函数效果不理想。分别使用summary函数和Box.test[11]函数获取两个模型残差的ARCH检验的信息,根据表5可知,拟合所得模型的残差均不具有ARCH效应,因此这两个模型对于可转债市场信息的提取都较好。Log Likelihood表示对数似然值,在参数估计中使用最大似然估计时便可得到,一般来讲Log Likelihood越大越好。两个函数的Log Likelihood分别为4900.265与4886.124,因此使用GARCH模型拟合可能会比较合适,模型的具体形式为式(8)。

表5 两种模型残差的ARCH效应检验
五、结论与建议
对可转债对数收益率的ARCH效应检验可知,可转债收益率具有ARCH效应,即残差序列在某些时间段波动较大,在某些时间段波动较小。使用EGARCH模型和TGARCH模型可知:可转债收益率没有杠杆效应,即可转债的收益率对于价格的大幅上升和大幅下降的反应相同。因此可转债可作为一种良好的金融工具,发挥更重要的作用。
此外根据表4GARCH族模型的系数,以GARCH模型和GARCH-M模型对可转换债券的对数收益率构建模型更为合适。根据对数似然值来看,使用GARCH模型更为合适。通过模型的具体形式,投资者可以对可转债市场进行预测,以作出买入或卖出的决策。
