舰载直升机指控系统试飞资源配置研究

2019-04-04袁大天于芳芳

指挥控制与仿真 2019年2期

袁大天,于芳芳,陈亮

(中国飞行试验研究院,陕西西安 710089)

舰载直升机在20世纪70年代已经发展到一定规模,根据任务需要,涉及反潜、反舰、警戒、侦察、电子战、搜救、运输、火力支援和反水雷等多种任务领域[1]。预警指挥类舰载直升机是以水面舰艇为搭载平台,满足了舰艇编队海上预警、指挥控制的需求,其可与舰载机、预警机、舰基指挥系统有效协同,扩展编队的立体对空观察体系,本文所描述的舰载直升机均指舰载预警直升机。

目前国内对舰载直升机的研究也形成了一定的规模,张智玮等分析了复杂电磁环境对舰载直升机战术数据链通信的数据率和误码率的影响,并从电磁兼容、电磁频谱管控、雷达合理组网部署等技术、战术层面对提高舰载防空探测设备预警能力提出了建议[2]。不少高校和研究院所对舰载直升机和指挥控制系统开展了理论仿真和数值模拟研究,主要关注了舰载直升机对空预警性能仿真分析[3-6],多架舰载直升机在反潜、预警任务中的编队配置研究[7-11],预警机指挥控制系统仿真建模与效能评估研究[12-16],对于舰载直升机的飞行试验,主要集中在起降包线,飞行品质方面的研究[17-19], 舰载指挥控制系统飞行试验方面的研究相对较少。王睿等针对预警机指挥控制系统中的威胁估计问题,提出了一种基于补偿直觉模糊神经网络(CIFNS)的威胁估计方法[20]；张西川等针对机载C3I系统建立了数据质量评估模型,将粗糙集和神经网络相结合,提出了一种试飞数据综合质量的计算方法[21]。

本文首先从前出距离、拦截对象、预警探测距离和拦截区域4个方面,分析了舰载直升机指挥控制系统的特点,建立以舰载直升机为指挥中心的对空预警/拦截引导模型,再基于上述模型,在一定的假设条件下,仿真计算了来袭目标和舰队拦截条件各因素之间的相互关系,得出在舰载直升机的前出距离、探测距离和舰队的拦截距离之间优化配置各指控要素的约束条件,从而为最大限度地利用现有的试验资源提供参考,提高舰载直升机指挥控制系统的试飞效率和质量。

1 舰载直升机指挥控制系统的特点

舰载直升机指挥控制系统利用机载电子设备,完成预警探测、目标识别、情报处理、数据融合、指挥控制功能,其可以为舰队武器在其最大射程上对来袭目标进行拦截提供预警拦截方案和反应时间。对于有陆基航空兵掩护的舰艇编队,拦截距离是自编队到陆基航空兵最大作战半径的距离;对于一般的驱护舰编队,拦截距离是编队中所装备的舰空导弹的最大射程;对于搭载舰载机的舰艇编队,拦截距离是自编队到舰载机拦截线的距离。

舰载直升机指挥控制系统飞行试验和使用方面考虑的重点因素在于:

1) 前出距离。由于舰载直升机在执行任务后或需要补给时,必须返回其搭载的搭载平台,因此前出不能太远,同时要保证留给舰队足够的预警距离和预警时间,因此其前出距离的限制条件较多。

2) 拦截对象。舰载直升机预警拦截对象主要为攻击机、舰载或机载反舰导弹,多为低空来袭目标。

3) 预警探测距离。受舰载直升机自身平台的限制,舰载直升机的预警探测距离相对较小。

4) 拦截区域。由于舰载机的作战半径一定,因此拦截线一般是以舰队为圆心,舰载机作战半径为半径的一个圆型或扇形区域。

2 舰载直升机指挥控制系统试飞资源配置

舰载直升机指挥控制系统飞行试验是一项复杂工程,其特点表现为多批、多路、多层次战术引导的综合试飞,导致飞行试验的科目、架次多,难度大,编队试飞密度高,飞行试验安全保证尤为重要,因此需要科学合理的规划试飞资源和试飞方案。这里的试飞资源特指为指控系统试飞配试的舰载机和目标机,资源配置则是针对舰载直升机的特点和舰队拦截条件以及威胁目标特点,配置前出距离、拦截速度、来袭速度等约束条件,采用科学的试验规程和评判准则来完成试验,在有限的条件和时段内获取尽可能多的高质量数据。

2.1 舰载直升机巡逻航线长度

巡逻航线长度是指舰载直升机在一定的高度、速度以及留空时间条件下的距载舰的活动半径,航线长度会直接影响舰队的预警时间和预警距离。我们采用标准矢量坐标,以直升机的载舰为矢量坐标的原点,即前出距离基准点,以载舰与主要威胁方向(如飞机、导弹来袭方向)的连线建立威胁轴,前出距离的另一端取威胁轴上的一点作为端点。由于舰艇编队各舰船的间距要远小于舰载直升机的预警距离,因此可以将整个编队视为一个点,从而来袭目标的威胁扇面角则是以整个编队点为圆心的扇面角,而不是针对某一艘舰船,即可以忽略编队队形变化对直升机预警效果的影响。

试验中,我们以单架舰载直升机在一个威胁扇面内的预警/拦截引导过程进行方案设计,舰载直升机预警/拦截引导模型如图1所示,以直升机所在位置为圆心B,以直升机预警雷达探测半径Dtc为半径画半圆,该半圆表示直升机的警戒区域。过圆心B垂直威胁轴作圆的一条直径,则直升机的警戒区域相对于载舰构成一个以威胁轴为扇面中心线的警戒扇面。

从直升机发现目标开始到舰载机到达拦截线与目标遭遇所需时间,可由下式估算出来:

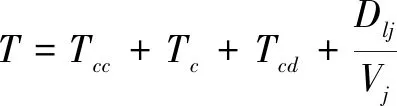
(1)

由图1所示的几何关系可得出:

DW=Dlj+VmT

(2)

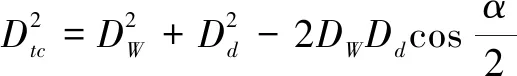
(3)

进而可求得舰载直升机对空预警时的最小前出距离为

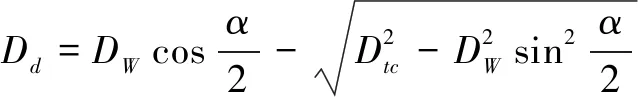
(4)

式中，DW为舰队在有直升机探测下的预警距离,单位km;Dlj为我方拦截机拦截线,单位单位km;Dd为直升机前出距离,单位km;Dtc为直升机探测距离,单位km;α为敌方武器对我编队的威胁扇面,单位°;Vm为来袭目标速度,单位m/s;Vj为我方拦截机速度,单位m/s;Tcc为舰载直升机指挥控制系统计算所需时间,单位s;Tc为我方通信时间,单位s;Tcd为我方拦截机出动时间,单位s。

2.2 舰载直升机航线高度

在试验航线高度的规划时,舰载直升机的航线高度涉及两个方面的因素。

首先,舰载直升机对海面和低空目标探测时,雷达发现目标的距离为几何直视距离,由于受地球曲率的影响,直升机的航线飞行高度应保证目标在直升机视距范围内,并且尽量保持在较高的高度,以充分发挥机载雷达的探测性能,因此,其航线飞行高度可由视距通信公式转化而来，即

(5)

式中:Hhx为直升机航线飞行高度,单位m;Hmb为来袭目标的飞行高度,单位m,当Hmb远小于Dtc时,上式可简化为

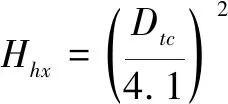
(6)

其次,考虑舰载直升机的实际使用环境,一般在海上飞行,同时飞行区域在舰队对空火力覆盖范围以内,因此,应保证其在海上最小安全飞行高度以上,尽可能保持较高的高度,以避免在实施对低空来袭目标拦截的误伤和直升机在撤离时自身故障导致的安全隐患。因此,舰载直升机指挥控制系统试验的航线高度应满足Hws≤Hhx≤Hrw,其中:Hws为避免舰队防空武器系统对低空来袭目标实施拦截时造成误伤的安全高度,Hrw为综合考虑任务类型、燃油量、留空时间等因素的任务执行高度。

2.3 配试目标配置模型

配试目标是指模拟来袭目标的试验资源,针对舰载直升机的使用特点,在试验资源的配置时,应考虑来袭目标、直升机自身限制条件以及我方拦截能力等方面的约束,这里重点针对配试目标资源的来袭速度进行分析,评估目标来袭速度的变化对直升机前出距离和拦截引导试飞的影响。

根据拦截引导模型可知,将式(3)代入式(4)得到来袭目标速度和直升机前出距离的关系:

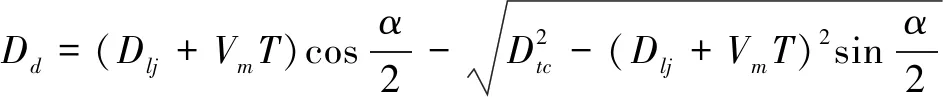
(7)

在该情况下,假定Dlj=150 km,Dtc=150 km,Vj=280 m/s,Tcc=10 s,Tc=5 s,Tcd=120 s,α=30°,在目标速度Vm取值200 m/s到1 000 m/s的范围内,对直升机前出距离进行计算,得到直升机前出距离与来袭目标速度的关系,计算结果如图2所示。

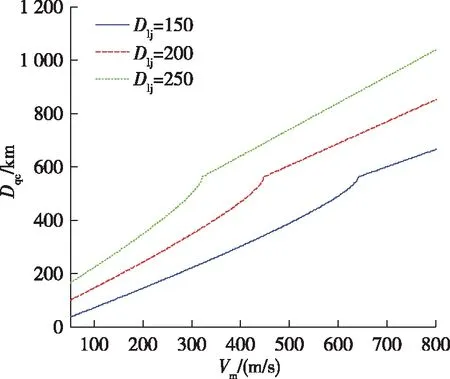
图2 直升机前出距离与来袭目标速度的关系

由图2可见,如果选取直升机探测距离为150 km、拦截机拦截线为150 km以及假定的其他各因素一定的前提下,直升机前出距离随着目标速度的增加呈明显上升的趋势,当目标速度为200 m/s的时候,前出距离为143 km左右,当目标速度增加到400 m/s的时候,前出距离上升为300 km左右。

图2中每条曲线均存在着一个拐点,当目标速度大于等于该拐点对应的速度值时,直升机的前出距离没有实数解。例如,图中实线的拐点对应速度为641 m/s,意味着,当目标速度大于641 m/s的时候,直升机的前出距离没有意义,已经无法实现早期预警、引导拦截的功能了。当前面的各假定因素发生变化的时候,该拐点的位置也会相应变化。

以直升机前出距离不大于图2中拐点对应的直升机的前出距离为限制条件(即保证直升机前出有意义),代入不同的拦截位置,计算在不同拦截位置时,前出距离和目标来袭速度的关系曲线,得到多组前出距离-来袭目标速度关系曲线,从而得到前出距离一定时,拦截位置和来袭速度的约束条件,其约束条件如图3所示,在直升机前出距离一定、拦截机速度一定的情况下,针对来袭目标速度的变化一一对应着目标拦截位置设置的最大值,随着来袭目标速度的增大,目标拦截位置呈下降的趋势,在约束条件下设计相应的试验科目,能够提高指挥控制系统试飞的有效性和成功率。

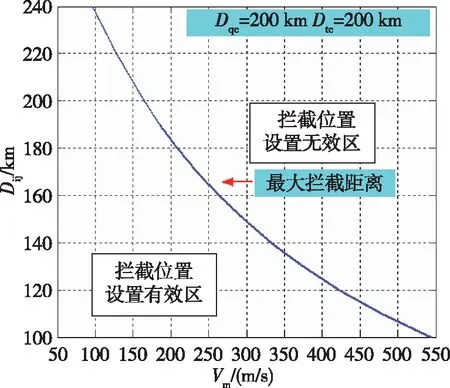
图3 目标拦截位置与目标来袭速度的约束条件

2.4 基于直升机自身能力的配置模型

这里,直升机自身能力主要是指其雷达探测能力,评估直升机自身探测能力的变化对其前出距离和拦截引导能力的影响。

我们假定在此情况下,Dlj=150 km,Vj=280 m/s,Vm=300 m/s,Tcc=10 s,Tc=3 s,Tcd=120 s,α=30°,直升机探测距离Dtc取值范围为50 km至180 km,将上述假设条件代入式(4),得出直升机探测距离与前出距离的关系,如图4所示。

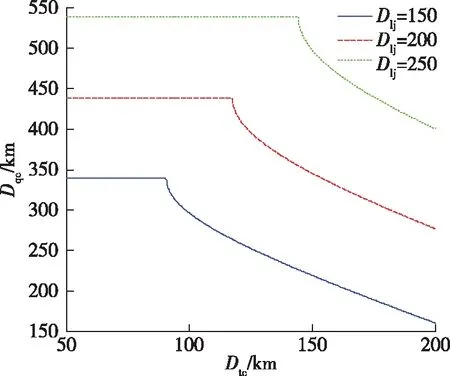
图4 直升机前出距离与其探测距离的关系

由图4可知,在假设我方拦截位置为150 km,以及其他假设条件一定的前提下,随着直升机雷达探测距离的增加或者称探测能力的提升,直升机前出距离呈现下降的趋势,探测距离为100 km时,前出距离为296 km左右,当探测距离提升至150 km时,前出距离减小至220 km左右。而且,可以看出图4中的曲线也都存在一个拐点,这说明,在这个拐点处,即当直升机探测距离小于该拐点对应的探测距离时,直升机前出距离没有实数解,即直升机已不能完成预警任务。

为了在直升机前出距离的限制条件下保证前出距离有实数解,选取不同的目标拦截位置,得到多组直升机探测距离和其前出距离的关系曲线,从而得到直升机前出距离一定时,目标拦截位置和直升机探测能力的约束条件,其约束条件如图5所示,即当我方拦截机选取不同拦截位置时,一一对应直升机探测距离的最小值,当直升机探测距离大于等于该临界值时,才能保证保证直升机前出有意义,能够为舰队提供足够的预警时间。

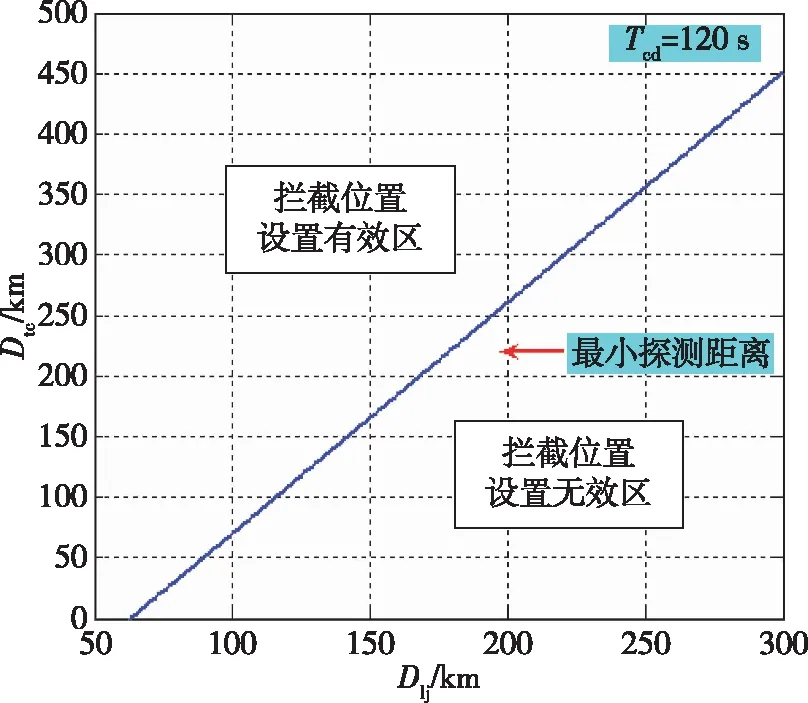
图5 直升机探测距离与目标拦截位置的约束条件

2.5 基于舰队拦截能力的配置模型

这里的拦截能力包含两个主要因素,即拦截机对目标的拦截位置和拦截机飞行速度,这两个自变量相互影响,基于舰队拦截能力的配置模型,主要是找出上述两个主要因素的变化与直升机前出距离的关系。

我们假定在此情况下,Dtc=150 km,Vm=300 m/s,Tcc=10 s,Tc=3 s,Tcd=120 s,α=30°,目标拦截位置Dlj取值范围为20 km至240 km,拦截机速度Vj取值范围为100 m/s至1 000 m/s,代入式(4)对直升机前出距离进行计算,得到直升机前出距离与目标拦截位置和拦截机速度之间的关系,计算结果如图6所示。

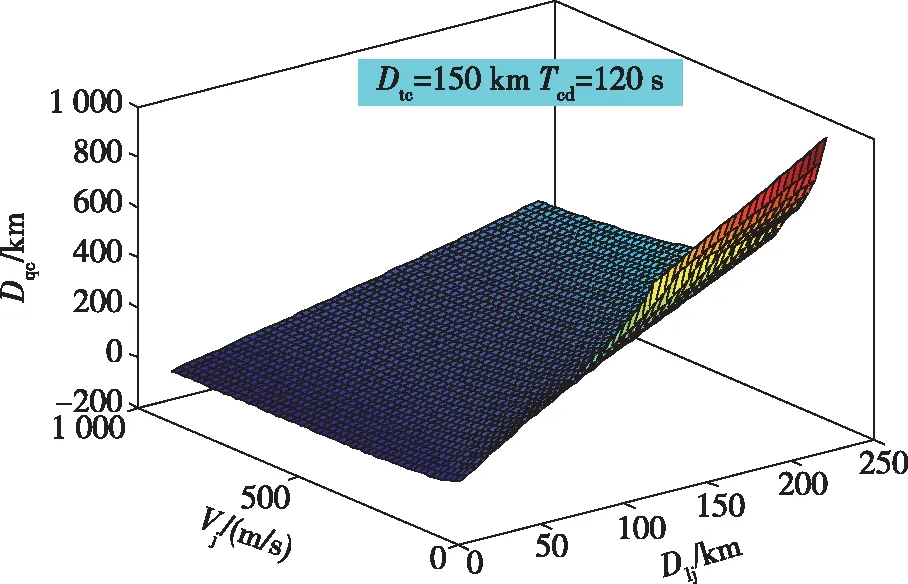
图6 直升机前出距离与舰队拦截能力的关系

由图6可知,在假设直升机探测距离为150 km以及其他假设条件一定的前提下,随着目标拦截位置的增加,直升机的前出距离呈现明显上升趋势,随着拦截机速度的增加,直升机前出距离会呈现微弱的下降趋势,图6中不同的目标拦截位置和拦截机速度,对应着不同的直升机前出距离值。

同样,从图6中可以看出,整个曲面的变化并非连续平滑变化,存在转折的部分,这是由一些非实数解造成的,这也就意味着,当目标拦截位置增加到一定的数值,当拦截机速度下降到一定数值时,直升机的前出距离没有实数解,前出无意义。

与前面的分析过程类似,为了在直升机前出距离限制条件下保证前出距离有实数解,设置不同的直升机探测距离,得到多组直升机探测距离和舰队拦截能力的关系曲面,从而得到直升机前出距离一定时,目标拦截位置、拦截机速度和直升机雷达探测能力的约束条件,其约束条件如图7所示。

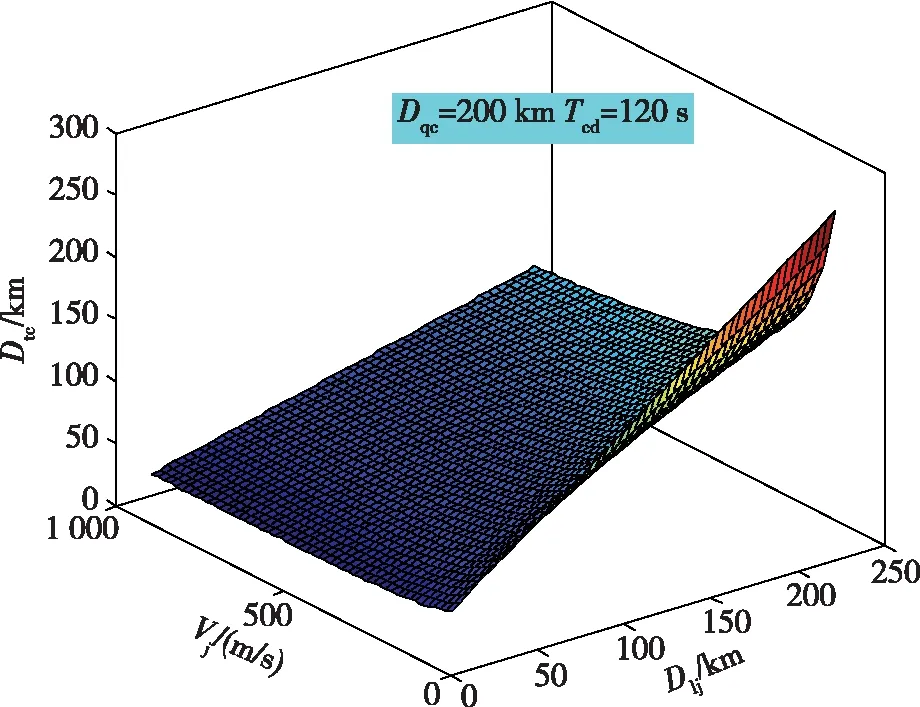
图7 直升机探测距离与舰队拦截能力的约束条件

上述各约束条件的分析对飞行试验方案的规划具有很大的参考价值,我们可以根据舰载直升机预警/拦截引导模型为基础,仿真计算出当直升机前出距离、指挥控制系统计算能力、我方拦截机出动时间等试验条件一定的情况下,直升机探测能力、我方拦截机速度、目标拦截位置、来袭目标速度之间的关系,得出其相互约束条件,从而根据现有的试验条件,有针对性地设计指挥控制系统的试验方案,从准备阶段、预警阶段、引导阶段进行试飞方案的规划,科学、合理地配置各类试验资源,尤其是针对舰载直升机的探测能力和我方舰队拦截能力,优化匹配不同的来袭目标类型,设计更多的试验点,获取更多的、更广泛的试验数据。