间歇采样转发式干扰的时频域辨识与抑制

周 超 刘泉华 胡 程

(北京理工大学信息与电子学院雷达技术研究所 北京 100081)

(北京市嵌入式实时信息处理技术重点实验室 北京 100081)

1 引言

基于数字射频存储器(Digital Radio Frequency Memory， DRFM)的间歇采样转发式干扰(Interrupted Sampling Repeater Jamming， ISRJ)，通过对雷达发射信号进行截获、延时与转发，可以形成相干干扰[1-4]。此类干扰与雷达发射信号部分相参，能够在信号处理中获得一定的增益，大大降低了对干扰机发射功率的需求，为干扰机的小型化和轻量化提供了基础[5]。因此，此类干扰机可搭载在无人机等小型平台上，配合蜂群战术形成主瓣干扰和多点源干扰，增加了雷达反对抗的难度。同时，利用DRFM的数字处理能力，ISRJ干扰机可以方便地对干扰参数进行调节，形成不同的干扰策略，对雷达构成了巨大威胁[6-8]。

对间歇采样转发式干扰的研究最早发表于2006年。王雪松等人[9，10]以及Sparrow等人[11]各自提出了间歇采样重复转发的干扰策略，并对其性能进行了分析(在文献[11]中称为(Chopping & Interleaving， C&I)。该干扰截取雷达发射信号的一个片段进行多次转发，然后重复截取-转发过程直至脉冲结束。此干扰信号经过脉冲压缩处理后，会在距离向上形成多个假目标群，每个假目标群由一个主假目标和多个对称分布的次假目标组成。通过对信号截取宽度和转发次数的设计，可以使其兼具压制和欺骗2种干扰效果。在此基础上，文献[10]还提出了间歇采样直接转发和间歇采样循环转发的干扰样式。其中，前者对截取的雷达发射信号仅进行一次转发，但是由于可以截取更多的信号切片，因此干扰能量更强，次假目标也更多；而循环转发式干扰在转发当前截获信号后，还会逆序转发之前截获的所有信号片段，其脉压后的假目标分布范围更广、分布规律也更不规则。此后，更多的研究人员对此类干扰的性能进行了分析，并进一步提出了改进的干扰策略。文献[12]讨论了干扰功率损失与截取比例的关系，分析了干扰功率损失对干扰效果的影响。文献[13]在介绍相参干扰原理及其压制机理的基础上，分析了相参干扰的压制距离。文献[14]针对线性调频信号，提出一种截取叠加与移频调制相结合的相参压制干扰，在增加假目标数量的同时可使假目标的位置发生变化，从而获得更佳的干扰效果。

而在雷达抗ISRJ技术方面，相应的研究还比较欠缺。经典的空域抗干扰方法存在难以获取纯净干扰协方差矩阵和合成波束主瓣性能恶化的难题，因此部分研究人员从波形设计和时频分析的角度进行了讨论。文献[15]提出使用脉间正交的编码波形进行干扰抑制，然而该方法仅能对抗脉间转发式干扰，对于脉内转发干扰则很难奏效。文献[16]针对DeChirp雷达，提出使用一种频域带通滤波器对干扰进行抑制，主要针对间歇采样重复转发和直接转发式干扰，对滤波的可行性进行了说明，但是对于噪声水平、干扰参数等因素对滤波器性能的影响，尚未分析。

针对上述问题，本文基于“辨识-剔除”[17，18]的干扰抑制思路，对间歇采样转发式干扰的抑制方法进行了研究。针对3种典型的干扰策略，在信号建模的基础上，推导了干扰信号脉冲压缩与时频分布的表达式；并根据其时频分布的特征差异，设计了干扰辨识流程；进而在获知目标位置的基础上，设计时频域滤波器进行干扰抑制；最后通过仿真对算法的有效性及不同信噪比条件下的性能进行了验证与分析。

2 间歇采样转发式干扰信号模型与干扰机理分析

2.1 干扰信号模型

典型间歇采样转发式干扰[9](直接转发、重复转发和循环转发)的工作原理如图1所示。其中，直接转发与重复转发式干扰都是对当前截获到的雷达信号进行转发，其差别仅在于转发的次数不同；该截获-转发过程会被重复多次，直到雷达脉冲结束。而循环转发式干扰在转发当前信号片段后，还会逆序转发此前截获的全部信号片段。

考虑3种干扰策略中转发次数和转发方式的差异，相应的干扰信号模型可以表示为：

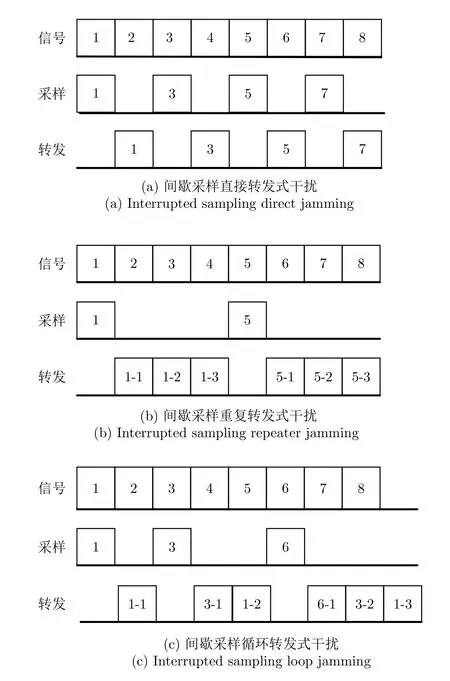
图1 间歇采样转发式干扰工作原理示意Fig.1 The principle of interrupted sampling repeater jamming

(1) 间歇采样直接转发式干扰

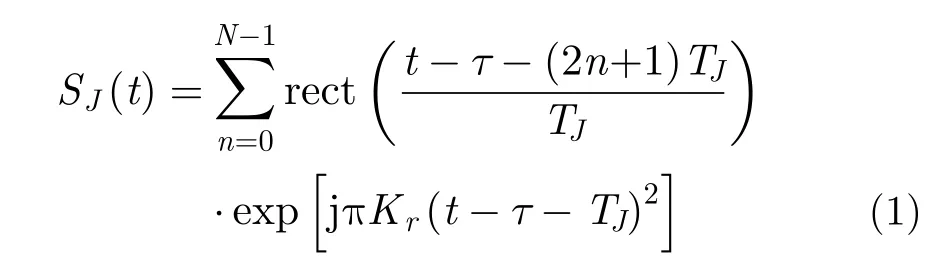
其中， r ect(⋅) 为矩形门函数，N为干扰切片个数，TJ为干扰切片宽度，Kr为发射信号调频率，τ为干扰机到雷达距离引入的延时。

(2) 间歇采样重复转发式干扰

其中，M为每个干扰切片被转发的次数，Tu=(M+1)⋅TJ为干扰机进行信号截获的时间间隔。

(3) 间歇采样循环转发式干扰

其中，a=(m(m+1))/2-1为相应切片的截获延时系数，b=(n(n+1))/2+n-1为每个切片进行转发时的延时系数。

2.2 干扰机理分析

由于间歇采样转发式干扰与雷达发射信号具有部分相参性，因此在进行脉冲压缩处理后，也可以获得一定的处理增益，形成假目标。以间歇采样直接转发式干扰为例，其脉冲压缩后的幅度响应可以表示为[19]

对式(4)分析可知：(1)因子 s in(Nφ)/sin(φ)由多个切片的叠加产生，当t=k/KrTu,k∈Z时可以取得极大值；(2)因子 sinc(KrTJ(t-TJ))由单个切片的脉冲压缩产生，其主瓣宽度为2 /(KrTJ)。

因此，对于间歇采样直接转发式干扰，其脉冲压缩结果表现为一个假目标群，群内存在2M+1个(对于直接转发式干扰即为3个)假目标，各假目标时间间隔1 /(KrTu)且幅度服从sinc函数调制。

对于间歇采样重复转发式干扰，其脉冲压缩结果相当于对式(4)的多次时移，表现为距离向上的多个假目标群，而每个假目标群的特征与直接转发式干扰相同。而对于间歇采样循环转发式干扰，由于不同切片只有在进行初次转发时才具有相同的转发时延，在进行第2次及更多次的转发时，其时延不同。因此脉冲压缩结果中存在一个假目标群与多个假目标，其中假目标群的分布特征同样可以用式(4)描述，而多个假目标则等同于时宽为TJ的Chirp信号的脉冲压缩结果。

3 间歇采样转发式干扰的时频域辨识与抑制

本节在脉冲压缩的基础上，使用短时傅里叶变换(Short Time Fourier Transform， STFT)获取干扰信号的时频分布，并讨论在此基础上进行干扰辨识与抑制的方法。

3.1 干扰信号的时频分析与辨识

为便于分析，首先仅考虑一个干扰切片的处理。在式(4)中，令N=1则可以得到1个切片的脉冲压缩结果

对该信号进行STFT，则可以表示为

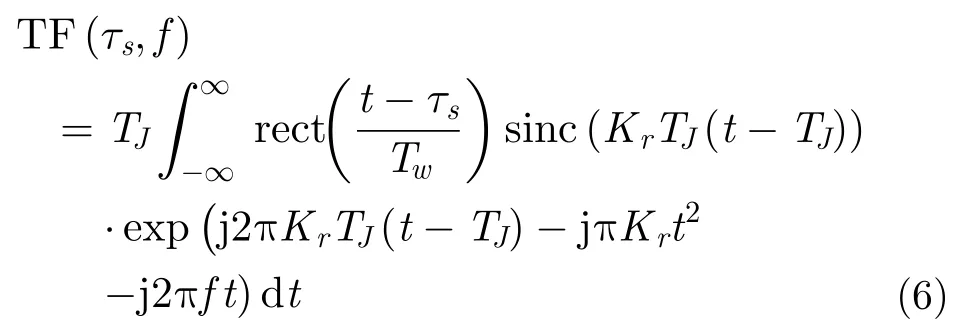
其中，τs为STFT的滑窗延时，Tw为滑窗宽度。

由于式(6)是一个Fresnel积分，不存在解析解，因此只能通过驻留相位定理给出近似结果。对该积分信号的相位进行求导并令导数为0，则可得时间与频率的关系

将式(7)代入式(5)，可得脉压峰值附近的信号频谱为

可得时频分布的幅度响应为

式(9)表明，对于一个干扰切片的脉压结果进行STFT，其在时域与频域都表现为sinc函数；其时间维的主瓣宽度为ΔT=1/KrTJ，而频率维的主瓣宽度则为ΔB=1/TJ。

对于间歇采样直接转发式干扰，其由多个延时相同的切片组成。经过脉冲压缩后，在距离向仅存在1个假目标群；但是由于其截获的不同切片具有不同的频率分量，因此在频率维表现为多个sinc函数。

在此基础上，对每一个切片进行多次转发，则构成了间歇采样重复转发式干扰。在这种干扰策略下，每一个假目标群都由多个延时相同的切片叠加而成；且不同的假目标群即对应于切片的多次转发。则其时频分布相当于对直接转发式干扰的频率维sinc函数在时域多次重复，进而形成时频面上呈网格分布的多个峰值。

而对于间歇采样循环转发式干扰，根据图1(c)所示工作原理可知：每个切片只有在进行第1次转发时，才具有相同的延时，此后对于不同的干扰切片，其转发延时都不相同。因此，其脉压结果的时频分布表现为时频域上“杂乱”分布的峰值，对于不同的距离门，其频域的sinc峰值个数不同。

根据以上特性，即可对间歇采样转发干扰的具体策略进行识别，设计的干扰策略辨识流程如图2所示。其具体步骤如下：

(1) 对于接收信号依次进行脉冲压缩和STFT处理；

(2) 基于时频变换结果，分析每个距离门内的峰值个数Mp、 峰值的3 dB宽度ΔF以及存在峰值的距离门个数Np；

(3) 根据上述参数即可进行干扰辨识：

(a) 若峰值的3 dB宽度与发射信号脉宽近似相等，即ΔF≈Tp，则为目标回波(一般情况下，ISRJ的截获时长小于脉宽的一半。因此只要ΔF＞Tp/2即可认为为目标)。

(b) 若峰值的3 dB宽度小于发射信号脉冲宽度，即ΔF＜Tp，且各距离门内峰值个数相等，则：

①Np=1时，为间歇采样直接转发式干扰；

②Np＞1时，为间歇采样重复转发式干扰；

(c) 若峰值的3 dB宽度小于发射信号脉冲宽度，即ΔF＜Tp，且各距离门内峰值个数不等，则为间歇采样循环转发式干扰。

需要说明的是：本文使用STFT进行时频分析仅作为一个示例，STFT截断窗的选取有可能导致时频平面中峰值的分布规律发生变化，进而影响干扰辨识的效果。然而不同时频分析方法的性能和参数选择问题并不在本文讨论的范围之内，其具体内容可以参考相应领域的专业文献[20]。

3.2 基于时频域带通滤波的干扰抑制

在干扰辨识的基础上，可以确定目标与干扰各自所在距离门。则通过设计时频域滤波器即可实现对干扰的抑制。假设经过干扰辨识后，可以确定目标所在距离门为r，则时频域滤波器可以定义为

其中，N为时频分布中时间维采样点数(距离门的总数)，i为时频域滤波器在每个距离门的列向量，其定义为

利用该滤波器响应与脉压结果的时频分布相乘，即可对干扰进行抑制。滤波过程表明：对于目标所在距离门，其信号保持不变；对于干扰所在距离门，其滤波输出等于该列最小值。若还需对脉压结果进行后续处理(如相参积累等)，则可对滤波输出进行逆STFT，即可得到干扰抑制后的脉压输出。

4 仿真结果与分析

本节通过仿真对上述干扰辨识与干扰抑制算法进行验证，并对算法性能进行分析。仿真中使用的部分参数如表1所示。

4.1 基于时频分析的干扰辨识算法仿真

图2 基于时频分析的干扰辨识流程Fig.2 The flow of jamming recognition with time-frequency analysis

在干扰辨识仿真试验中，定义信号类型变量s，其取值与信号类型的对应关系为：

(1)s=0，目标回波；

(2)s=1，间歇采样直接转发式干扰；

(3)s=2，间歇采样重复转发式干扰；

(4)s=3，间歇采样循环转发式干扰。

对于上述目标与干扰信号，其相应的脉冲压缩结果与时频分布分别如图3和图4所示。结合仿真结果与前文分析可知：目标与干扰在时频域具有可分性，且不同干扰策略的时频分布特征不同。基于该特征差异，可以进行干扰辨识。

其具体的仿真步骤如下：

(1) 对于一个固定的SNR(这里的信号泛指目标与干扰)，任意生成一个0～4之间的整数，并根据前文对应关系生成雷达接收信号；

(2) 利用干扰辨识算法对接收信号进行处理，并记录辨识结果：若辨识结果与信号类型相同，则记为一次正确辨识；

(3) 对上述过程进行1000次重复仿真，统计当前SNR下的正确识别率；

(4) 调整SNR，对上述步骤(1)-步骤(3)进行重复，得到不同SNR下的辨识算法性能曲线。

相应的仿真结果如图5所示，可知当原始回波的SNR大于-3 dB时，正确辨识率可达90%以上。

表1 干扰辨识与抑制仿真参数Tab.1 Simulation parameters for jamming recognition and suppression

4.2 基于时频域滤波的干扰抑制算法仿真

对于不同的干扰策略，其典型的干扰抑制效果仿真如图6所示。在干扰抑制前，设置的信干比(Signal to Jamming Ratio， SJR)为-15 dB， SNR为-10 dB。经过脉冲压缩处理后，SNR约为20 dB，而对于不同的干扰策略，峰值SJR约为-3～0 dB。从仿真结果中可以看出：对于不同的干扰策略，算法都可以有效地对干扰进行抑制；其获得的信干噪比(Signal to Noise and Jamming Ratio， SJNR)改善约为18 dB。

图3 目标与干扰的脉冲压缩结果Fig.3 Pulse compression of target and jamming signal

图4 目标与干扰脉压结果的时频分布Fig.4 The time-frequency distribution of pulse compression result of target and jamming signal

5 结束语

基于DRFM器件的间歇采样转发式干扰兼具压制和欺骗2种干扰效果，其干扰参数灵活可变，对雷达探测构成了巨大威胁。本文对此类干扰的辨识与抑制方法进行了研究：基于脉压结果的时频分布，设计了干扰辨识流程；并通过仿真验证了该辨识算法的性能，结果表明：在原始回波SNR大于-3 dB的条件下，正确辨识率可达90%以上。相对于已有算法，本文方法将干扰脉压后的时频分布特征总结为先验知识，无需数据训练即可直接进行干扰辨识。在此基础上，提出一种基于时频域滤波的干扰抑制算法，该算法可以在目标与干扰脉压后距离可分的情况下，对不同策略的干扰进行有效抑制，其典型的信干噪比改善可达18 dB。

虽然本文研究仅针对单部ISRJ干扰机进行了讨论，但是对于多部干扰机形成的多点源干扰环境，在干扰与目标脉压后距离可分的前提下，本文方法仍然有效。基于脉冲压缩波形的距离高分辨特性，结合现代雷达的自动检测跟踪功能，本文认为实际环境中干扰脉压峰值长时间遮蔽目标峰值的概率非常小。

图5 干扰辨识仿真结果Fig.5 Simulation results of jamming recognition

图6 不同干扰策略下的干扰抑制结果Fig.6 Jamming suppression results of different jamming strategies