轮间距与双轮共转对飞机起落架摆振的影响分析
2019-04-03朱红民
冯 飞, 罗 波, 张 策, 朱红民
(中国运载火箭技术研究院,北京 100076)
前轮摆振,是飞机地面滑行过程中出现的常见现象[1]。尽管已被研究近一个世纪,现代飞机在研制和使用过程中仍无法完全避免摆振问题。自Broulhiet最早在汽车领域发现该问题后,前轮摆振在学术界普遍被认为是一种包含轮胎变形、支柱扭转变形与侧向变形等在内的多自由度耦合振动稳定性问题[2-3]。von Schlippe等[4-6],提出了轮胎的点接触模型与张线模型,奠定了摆振轮胎理论的基础,指出了轮胎参数对摆振稳定性的影响。20世纪50年代起在美国Langley研究中心[7]开展的大量地面滑行试验,为摆振的理论发展提供了基础,起落架的结构参数的影响被学者广泛研究。至20世纪80年代,起落架摆振的线性模型发展趋于完善,研究更多地关注了起落架与机体弹性、起落架与机身的联接等因素的影响。此后,以平方阻尼、库伦摩擦、结构间隙为代表的等非线性参数,成为前轮摆振研究的热点[8-12]。Somieski指出,线性模型在精确预测起落架前轮系统的摆振行为时是无力的。21世纪起,随着应用分岔理论(Applied Bifurcation Method)的逐渐完善,Thota等[13-15]提出了摆振分岔分析的基本步骤,采用分岔理论对非线性模型进行摆振分析成为前沿研究方向[16-17]。
本文提出了较为完善的摆振分岔分析方法,对包含轮胎变形、支柱扭转、支柱侧向弯曲等自由度在内的双轮起落架非线性模型进行了研究,并分析了轮间距、双轮共转对摆振稳定性的影响。研究成果可用于指导飞机前起落架设计。
1 摆振动力学模型
1.1 坐标系与自由度
如图1所示,一个垂向承载Fz的双轮前起落架。安装点离地高度Lg,起落架跟随机身以恒定速度V,通过半径为R、间距为D的两个机轮在跑道上直线滑行。

图1 双轮起落架摆振模型示意图Fig.1 Schematic of a dual-wheel aircraft landing gear
滑行方向的反向定义为起落架坐标轴的X轴,水平向右为Y轴,垂向向上为Z轴。起落架支柱扭转的平衡位置为中立,故不考虑机身的侧向运动。在平稳滑行过程中,飞机没有垂向位移,且起落架缓冲器的行程是不变的,故不考虑起落架的垂向位移。
(1)起落架支柱可绕定向轴S转动,转角为θ。
(2)绕X轴方向,起落架支柱存在侧向弯曲变形ψ。
(3)左右两个轮胎的侧向位移λ1和λ2用于描述轮胎的变形。
(4)轮轴扭转变形的自由度ξ,用于共转双轮之间的相互作用。如将轮轴扭转变形ξ至零,则表征双轮不共转。
1.2 动力学方程
双轮共转的摆振动力学方程,可表述为式(1)~式(5)。
(1)
(2)
(3)
(4)
(5)
式(1)和式(2)分别为起落架支柱扭转与侧向弯曲自由度的平衡方程;式(3)和式(4)为基于von Schlippe的张线理论的轮胎变形协调方程;式(5)为轮轴扭转变形自由度的平衡方程。
在后文方程的描述中,为便于书写,略去表征左右轮胎的下角标i。
1.2.1起落架支柱扭转方程

Mkθ=kθ·θ
(6)
(7)
式中:MF为轮胎作用于支柱扭转自由度的组合力矩,包含轮胎非线性扭转回正力矩Mkδ和轮胎非线性侧向回复力Fkλ产生的力矩,如式(8)
MF=Mkδ+Fkλ·eeff
(8)
轮胎非线性扭转回正力矩Mkδ用式(9)进行描述。在轮胎的侧滑极限δm范围内,回正力矩Mkδ随侧偏角δ按正弦规律变化;在侧滑极限δm范围外,轮胎发生了侧滑,回正力矩Mkδ等于零。
(9)
轮胎非线性侧向回复力Fkλ根据实验数据进行拟合,可表达为轮胎侧向刚度系数kλ、侧偏角δ和垂向载荷FZ的函数,如式(10)所示
Fkλ=kλarctan(7.0 tanδ)cos(0.95arctan(7.0 tanδ))FZ(10)

(11)
(12)
定向轴S与Z轴之间的前倾角φ,使得机轮的转向角ζ并不严格等于起落架支柱的扭转角θ,而是满足式(13)所述的关系
ζ=θcos(φ)
(13)
定向轴S距离机轮的轮心存在机械稳定距e。前倾角φ的存在产生了几何稳定距eeff,使得等效稳定距满足式(14)
eeff=ecosφ+(R+esinφ)tanφ
(14)

(15)
在起落架滑行过程中,左右机轮承受的垂向载荷FZ1和FZ2并不相等。根据力矩平衡关系[19],可按式(16)进行计算
(16)
式中:kv为轮胎的垂向压缩刚度;γ为支柱前倾角导致的轮盘平面侧倾角,可表达为式(17)
γ=θsin(φ)
(17)
1.2.2起落架支柱侧向弯曲变形方程

Mkψ=kψ·ψ
(18)
(19)
式中:Mλψ为轮胎非线性侧向回复力产生的力矩,如式(20)所示
Mλψ=FkλLgcos(ζ)cos(φ)
(20)

(21)
1.2.3轮胎变形协调方程
起落架支柱的扭转与侧向弯曲变形,通过轮胎的侧向力进行耦合作用。机轮的轮胎模型基于张线理论建立,以轮胎触地点中心线的侧向位移λ和侧偏角δ作为轮胎变形量。其中,轮胎的侧偏角δ被定义为轮胎触地点中心线的侧向位移λ和轮胎松弛长度σ的函数,可表达为式(22)
δ=arctan(λ/σ)
(22)
轮胎相关的其余力和力矩见1.2.1节,不再赘述。
1.2.4轮轴扭转变形自由度的平衡方程
式(5)描述了考虑双轮共转条件下的轮轴扭转变形。如将变量ξ至零,则表征双轮不共转。
1.3 参数取值与延拓范围
文中参数的含义与取值参见表1[20]。参数取值基于A320的前起落架数据。考虑到参数分岔图像的完整性,部分参数的选取,如前向滑行速度等,可能超过实际的取值范围。

表1 参数取值表Tab.1 Value of parateters
2 摆振分岔分析方法
摆振动力学方程组,可以改写为式(23)的形式
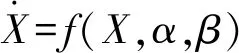
(23)

摆振分岔分析步骤如下:
步骤1确定平衡点。
在不考虑转弯的前向滑行摆振分析中,希望出现的系统平衡状态为各状态变量中立的零平衡状态,即起落架支柱无扭转角与侧向弯曲变形,轮胎触地点中心线无侧向位移等。故在摆振分岔分析中,仅分析零平衡状态下的稳定性及相应Hopf分岔(及周期振荡解)的分岔特性。
步骤2寻找Hopf分岔点。
在确定平衡状态后,固定包含第二个控制参数β在内的其余所有参数不变,连续地变换第一个控制参数α的取值,计算控制参数α不同取值情况下,系统零平衡状态的所有特征值。
若Jacobi矩阵的所有特征值λ1,λ2,…,λn满足Reλ<0,零平衡状态则是稳定的。随着控制参数α的连续变化,所有特征值λ1,λ2,…,λn也连续变化。若发现控制参数在某个取值α=αH时,某一对特征值出现了Reλi,j=0情况,则系统出现了Hopf分岔。并称控制参数α=αH为系统零平衡状态的Hopf分岔点,简称为Hopf分岔点。
步骤3Hopf分岔点的单参数延拓。
选取任一Hopf分岔点,仍仅连续变换第一个控制参数α的取值,采用延拓算法,对各特征量随控制参数的变化进行计算。
图2为采用前向滑行速度为控制变量进行单参数延拓的计算结果。
步骤4Hopf分岔点的双参数延拓。
在获得第一个控制参数α的Hopf分岔点α=αH的基础上,增加第二个控制参数β,求解二维控制参数(α,β)平面内的Hopf分支线。

图2 Hopf分岔特征量随滑行速度的变化曲线Fig.2 Curves of characteristic parameter varying with forward speed
图3为采用前向滑行速度和垂向载荷为控制变量进行双参数延拓的计算结果。观察可得:两条Hopf分岔曲线交于2点,称为双Hopf分岔点,图中表示为“HH”;其中,一条封闭的Hopf分岔点上出现了2个Bautin分岔点,图中表示为“B”。Bautin分岔点意味着在当前点Hopf分岔曲线发生了分岔。分岔出的一分支(图2中两个Bautin分支点之间上方的曲线)为不稳定的极限环的边界,摆振分岔分析并不关心;另一支为稳定的极限环的边界,表征摆振稳定区和不稳定区的边界,有待进一步求解[21]。

图3 以垂向载荷、滑行速度为控制变量的分岔图(1)Fig.3 Bifurcation map in vertical load-forward speed plane(1)
步骤5Bautin分岔点的双参数延拓。
以Bautin分岔点为起点,延拓计算Hopf分支线分岔后的稳定分支。
如图4所示,新计算获得的分支线即摆振稳定区的边界。由此,摆振分岔计算的二维相图完成;获得了摆振稳定与非稳定区域图,详见图5。如图5所示,起落架摆振在相图上可直观地进行分辨,包括以支柱扭转为主体的扭转摆振和以支柱侧向弯曲变形为主体的侧向弯曲摆振(简称侧向摆振)。
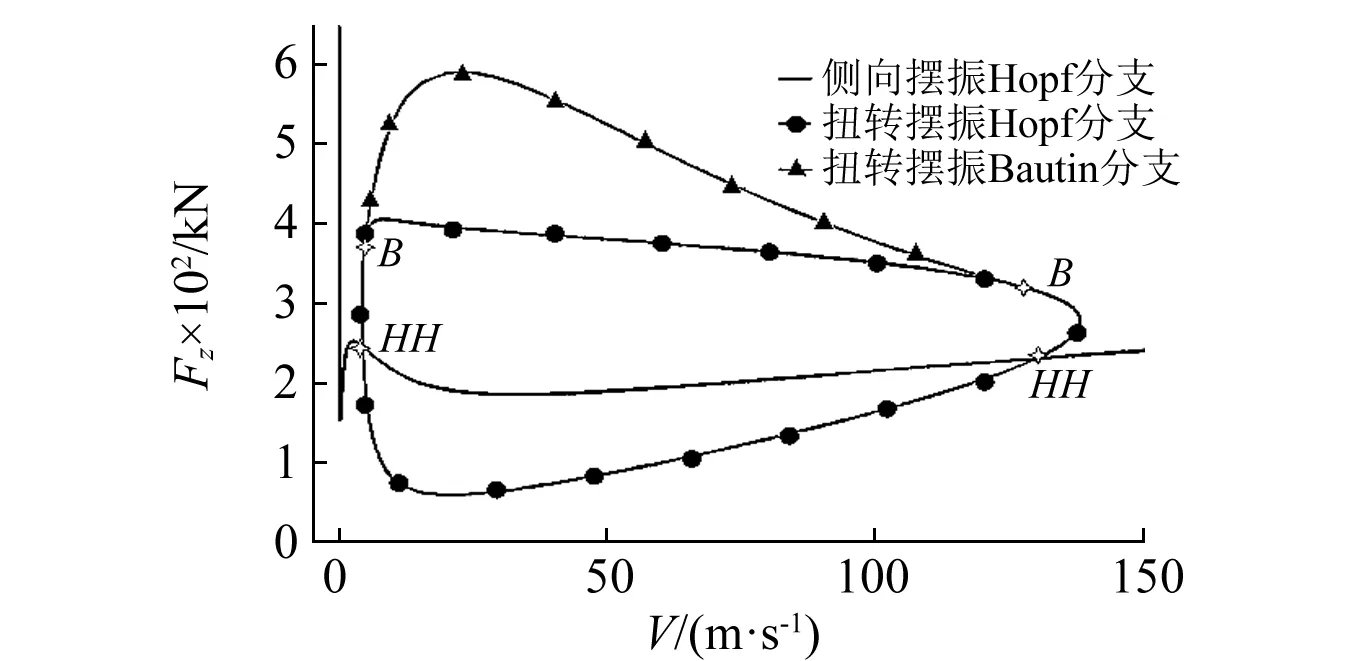
图4 以垂向载荷、滑行速度为控制变量的分岔图(2)Fig.3 Bifurcation map in vertical load-forward speed plane(2)
本章仅给出摆振分岔计算的基本流程,不给出分岔计算的具体理论[21]。

图5 典型的摆振分岔图Fig.5 Typical bifurcation map of shimmy analysis
3 摆振参数分析
3.1 轮间距对摆振稳定区的影响
图6和图7给出了轮间距D从0~0.4 m内不同取值的扭转与侧向摆振区域。

图6 轮间距对扭转摆振区域的影响Fig.6 Effect of tyre-distance on torsional shimmy bifurcation area
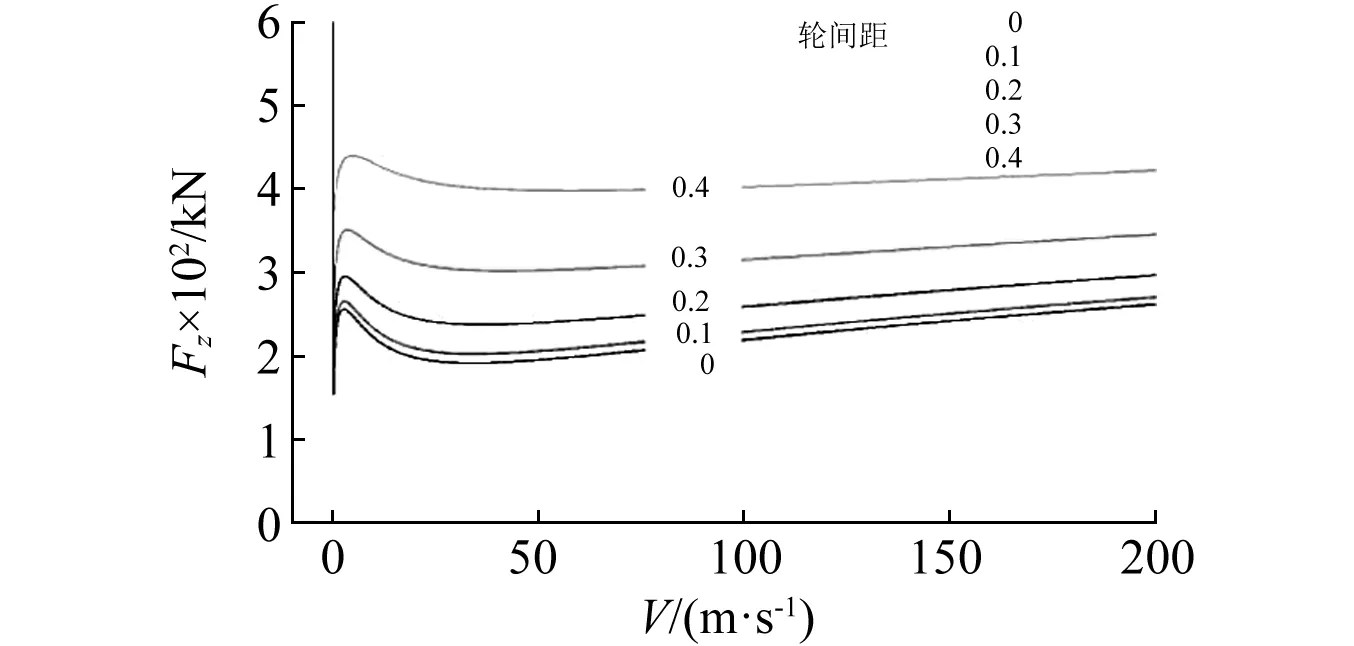
图7 轮间距对扭转摆振区域的影响Fig.7 Effect of tyre-distance on lateral shimmy bifurcation area
如图6和图7所示,随着轮间距的增大,扭转摆振区域产生了一定的增加,侧向摆振区域则趋于减小。轮间距的增大,变相提高了支柱的侧向弯曲刚度,进而对侧向摆振起到抑制作用,对扭转摆振则刚好相反。
除轮间距小于0.1 m时带来的差异几乎可以忽略外,轮间距变化导致摆振区域的差异是很明显的。并且,轮间距其取值越大,其等幅增量引起的变化越为显著。轮间距为0.4 m时的扭转摆振区域面积是零轮间距情况的约2.5倍,侧向摆振区域面积约为2倍。
在维持中低速和中低垂向载荷区域稳定性不变的同时,扭转摆振区域随着轮间距的增大,向高速高垂向载荷区域延伸扩展。侧向摆振区域则向高垂向载荷区域拓展。
图8 轮间距对摆振区域的影响Fig.8 Effect of tyre-distance on shimmy bifurcation area
图8给出了轮间距为0.5 m时的摆振区域。相比不大于0.4 m的情况,其摆振区域截然不同。如图8所示,轮间距为0.5 m的情况下,扭转摆振与侧向摆振的Hopf分支线完全融合。原有的两组Hopf分岔曲线组成一条自相交的复杂曲线,表征了摆振的发生区域。在整条曲线的右上方,包含曲线左端的封闭区域,均会发生摆振现象。由于拓扑形式的改变,摆振类型无法严格地进行划分。
3.2 双轮共转对摆振稳定区的影响
为综合考察双轮共转对摆振区域的影响,计算轮间距分别为0.1 m,0.2 m和0.3 m时,采用双轮共转的摆振区域图,与相应的不共转情况进行对比,如图9所示。

图9 双轮共转对摆振稳定区的影响Fig.9 Effect of co-rotation wheels on shimmy bifurcation area
如图9所示,在轮间距0.1 m的情况下,采取双轮共转的摆振稳定区与不共转几乎完全重合;随着轮间距的逐渐增大,双轮共转一定程度上减小了高滑行速度下的扭转摆振非稳定区,对于侧向摆振区域则几乎没有影响。
4 结 论
本文建立了包含轮胎变形、支柱结构变形等自由度的双轮起落架非线性摆振动力学模型,给出了一套采用分岔分析方法进行非线性摆振稳定性研究的方法,并对轮间距、双轮共转对摆振稳定性的影响进行了详细分析。
(1)轮间距的增加变相提高了支柱的侧向弯曲刚度,能减小侧向摆振的发生区域,增大扭转摆振区域。当轮间距超过某一临界值时,轮间距会导致摆振区域拓扑结构的改变。
(2)采用双轮共转,对起落架的扭转防摆在一定程度上起到积极的作用。在采用相对较大的轮间距时,双轮共转对扭转摆振区域的影响更为明显。对小轮距的起落架,双轮共转的作用是很有限的。
