高传递损失基座阻抗优化设计法
2019-04-03杨德庆吴秉鸿
杨 康 , 杨德庆,2, 吴秉鸿
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2. 高新船舶与深海开发装备协同创新中心 海洋工程国家重点实验室,上海 200240)
舰艇内部机电设备等机械振动源是引起船体水下辐射噪声的主要因素,对舰船生命力及战术性能有重要影响。通过机械阻抗来反映结构在外部激励作用下动态响应特征以及振动传递规律的阻抗技术在工程实际中已广泛应用,阻抗特性是结构隔振特性的重要指标,直接反映结构减振性能优劣。熊琳[1]通过理论及试验研究发现,基座阻抗值幅值越大,则对机械设备传递给船体的振动能量的阻碍作用越大,其隔振作用越强。传递损失是反映隔振装置隔振性能的常用指标,高传递损失意味着隔振装置对振动的隔离性能好,因此高传递损失基座设计是设计人员追求的目标。
为减小机械动力设备通过基座传递到舰艇外壳的振动能量,提高基座的机械输入阻抗是可行方法,这包括调节基座面板/腹板/肘板的厚度、在基座上附加阻振方钢和贴敷阻尼材料等措施。工程实际应用中,通过基座机械阻抗计算可以近似得到基座振级落差,作为减振以及声学优化重要设计参数。目前基座阻抗的计算方法主要可分为理论解析法、有限元法以及阻抗测试法等,较难采用纯理论解析方法计算其机械阻抗。
理论解析法包括四端参数振动分析技术、动态子结构法以及弹性体阻抗分析法等。谢志强[2]基于四端参数法,证明了实船基座阻抗的大小直接影响隔振装置的隔振效果以及基座的振动量级。动态子结构法主要分为导纳/阻抗综合法和模态阻抗综合法。Petersson[3-4]等针对系统的子结构导纳矩阵,对柔性隔振系统的振动传递特性进行了研究。孙建刚等[5]对典型基座振动形态及阻抗特性进行了研究,分析了典型船舶基座结构在各个特征频率段内的振动模式和物理模型。庞福振等[6]以船体基座振动加速度为激励,分析船体结构动力学响应,验证了阻抗分析法的有效性。吴文伟等[7]以大型基座为研究对象,根据基座在不同频率段范围内的实际动力学特性建立了相应的数学物理模型,结合机械阻抗的机理分析方法以及复合组件系统的机械阻抗计算原理,得到了大型基座的机械阻抗在不同频段内的简化估算公式。毛亮等[8]针对两种新型复合材料基座结构设计方案建立数值模型,分析了基座结构刚度和强度的影响参数并优化了夹芯复合材料基座的结构形式。周海波等[9]以悬臂型基座为研究对象,基于阻抗失配原理进行了悬臂型基座的结构参数优化研究。Goyder等[10]对一维隔振系统单扰动源的无限大基础结构进行研究,建立了单支承结构的导纳模型。王小龙等[11]以圆筒型复合材料基座为研究对象,结合基座阻抗理论分析,研究了芯材阻尼、嵌入连接环质量以及内外筒壁厚度比变化对基座减振效果的影响规律。阻抗测试方法包括激振方法、阻抗测量和数据处理等内容。Pradhan等[12]通过激振试验研究了不同分层土壤上基座的动态响应,试验结果验证了基于阻抗模型的理论分析结果。Madhav等[13]对复合材料合成沉箱基座开展了理论与试验对比研究。
本文从理论上对国内外阻抗计算方法进行了归纳,引入阻抗级的概念,通过对某水面舰船的有限元模拟计算,提出利用阻抗级描述舰船基座的减振效果。通过模拟实船基座,以基座有效频段范围内的总阻抗级作为约束条件,对基座进行了阻抗优化设计,获得高传递损失基座。研究了不同位置布置方钢对基座结构输入机械阻抗的影响。基于Isight平台的近似代理模型优化方法,以方钢布置尺寸为变量实现了多因子复合阻振优化设计,为建立高传递损失基座优化设计方法提供参考。
1 基座机械阻抗的计算方法
1.1 阻抗定义及计算
机械阻抗[14-15]来源于电路理论中的电阻抗特性,基于机电系统比拟提出了研究结构系统动态特性的机械阻抗方法。对于线性定常系统,机械阻抗传统定义为简谐激励与由其所引起的简谐运动响应两者之比的复数形式。广义机械阻抗定义为系统激励与引起响应的傅氏变换或拉氏变换的比值。
由于常用位移、速度以及加速度来描述系统的动态响应,因此机械阻抗分为位移阻抗(又叫动刚度)、速度阻抗和加速度阻抗(又叫有效质量)三种。以位移为例,系统的位移机械阻抗Z,可表示为
(1)
式中:Z为结构位移阻抗;F为力;X为施力点的位移响应。
1.2 点阻抗与传递阻抗
根据阻抗的定义,若振动响应是激振点的,称为驱动点阻抗简称点阻抗;若振动响应不是激振点的,称为传递阻抗或跨点阻抗,表示为
(2)
式中:Fi为作用在i点的激振力;Xj为作用在j点的振动响应,而i点的点阻抗表示为
(3)
点阻抗可以分为直接阻抗和交叉阻抗,前者是指振动响应与激振力同方向,后者则是不同方向的情况。
直接阻抗
(4)
交叉阻抗
(5)
2 基于阻抗级的减振效果描述
基座隔振主要是通过基座结构弹性变形减小振动的传递,目前主要评价指标一般选用传递率、插入损失以及振级落差等,近年来振动功率流及振动功率流落差的概念也逐渐成为评价隔振性能的重要指标[16-18]。隔振评估是为了获取隔振装置对振动输入的衰减量。以加速度为例,系统受迫振动时激励处加速度幅值记为a0,传递到其它部位的响应幅值记为an,则有振动传递率
(6)
振级落差VDL(Vibration Difference Level)的表达式为
(7)
式中:L1为激振点处加速度级;L2为评价点处加速度级;aref为加速度参考值,aref=10-6m/s2。
振级落差与振动传递率之间的关系为
(8)
以阻抗表示振动传递特性的公式为
(9)
式中:Y0为原点导纳;Yn为传递导纳;Z0为原点阻抗;Zn为传递阻抗。
定义阻抗级Lz为
(10)
式中:Zref定义为基准阻抗,为使评价指标相对明显,本文取Zref=10-1N/(m/s-2),这区别于常规的Zref1 N/(m/s-2)。
振级落差与传递率、振级及阻抗级的关系
(11)
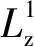
(12)

阻抗级与振级间的关系为(以加速度为例)
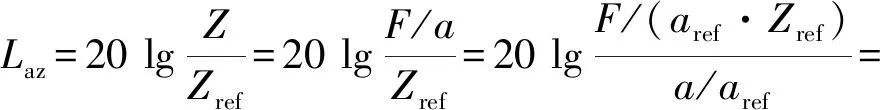
(13)
对于单位力激励下的原点阻抗级,F=1,式(13)简化为Laz=140-La。可见,阻抗级与振级是相反关系,阻抗级越大,振级越小,增大系统阻抗会减小系统的振动。

(14)
式中:Li为某一频率处的振级;N为频率点总数。
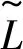
(15)
(16)
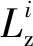
(17)
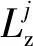

表1 描述振动传递特性的各种指标辨析
3 舱段基座阻抗计算实例
本文选取某水面舰船的舱段模型进行有限元模拟,计算对比基座各类评价指标。舱段实际结构模型如图1和图2所示,采取单位力在基座上如图3所示的相应激振位置进行激励,选取如图4所示的12个位置作为评价点。采用直接积分法进行1/3倍频程频响分析,计算得到基座加速度响应、机械阻抗和振级落差。

图1 舱段模型Fig.1 Cabin section model
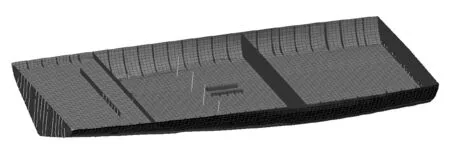
图2 舱段基座模型Fig.2 Cabin base model

图3 激励点位置Fig.3 Incentive points

图4 评价点位置Fig.4 Evaluation points
3.1 单点激励-单点拾振
在图3的激振点位置中选取某一点激振,在图4评价点位置中选取一点评价,计算得到该位置的振动加速度响应。通过数据处理得到单点激振单点拾振时激振点与评价点加速度振级、原点阻抗级与传递阻抗级,进而计算得到加速度振级落差与阻抗级落差,如图5~图7所示。可以发现,基座系统的加速度振级落差与阻抗级落差相同,与理论计算相符,如图7所示加速度振级落差与阻抗级落差曲线重合,表明以单点激振单点拾振来分析结构振动传递特性时,可以通过阻抗级来准确地描述舱段内基座系统的减振性能。
3.2 单点激励-多点拾振
选取图3激振点位置中各点分别进行激振,通过Abaqus有限元软件计算得到各评价点位置振动加速度响应。然后利用相应计算公式对数据进行处理,得到在不同激励点激励下激振点加速度振级与评价点平均加速度振级,原点阻抗级以及平均传递阻抗级,进而得到如图8~图13所示的不同位置激励时的加速度振级落差与阻抗级落差。可以看出,在低频1~63 Hz频率范围内,不同位置激励时加速度振级落差与阻抗级落差十分相近,因此加速度振级落差近似可以用阻抗级落差来代替进行减振效果描述。中高频段(200 Hz以上)内,加速度振级落差与阻抗级落差曲线也比较相似,近似成正比例关系,整体来看利用阻抗级的概念可以较为准确地描述结构减振效果。

图5 激振点与评价点加速度振级Fig.5 The acceleration levels of the excitation point and the evaluation point

图6 原点阻抗级与传递阻抗级Fig.6 The origin impedance level and the transfer impedance level

图7 加速度振级落差与阻抗级落差数值验算Fig.7 The numerical calculation of level differences of the acceleration and the impedance
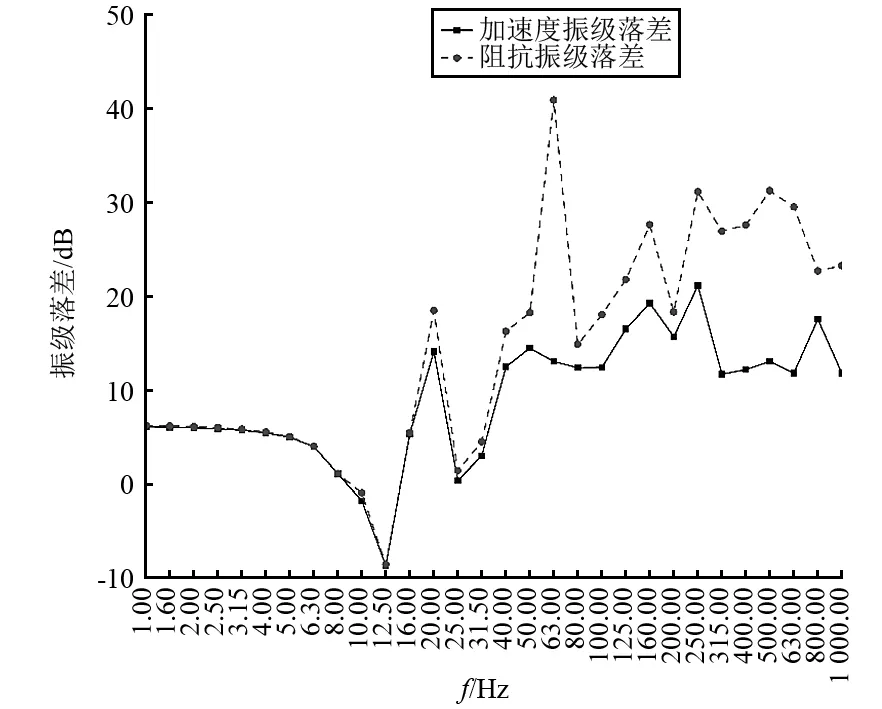
图8 1号位置激励振级落差Fig.8 Vibration level difference of position 1

图9 2号位置激励振级落差Fig.9 Vibration level difference of position 2

图10 3号位置激励振级落差Fig.10 Vibration level difference of position 3

图11 4号位置激励振级落差 Fig.11 Vibration level difference of position 4
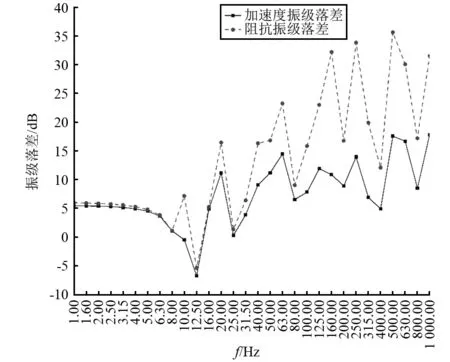
图12 5号位置激励振级落差 Fig.12 Vibration level difference of position 5
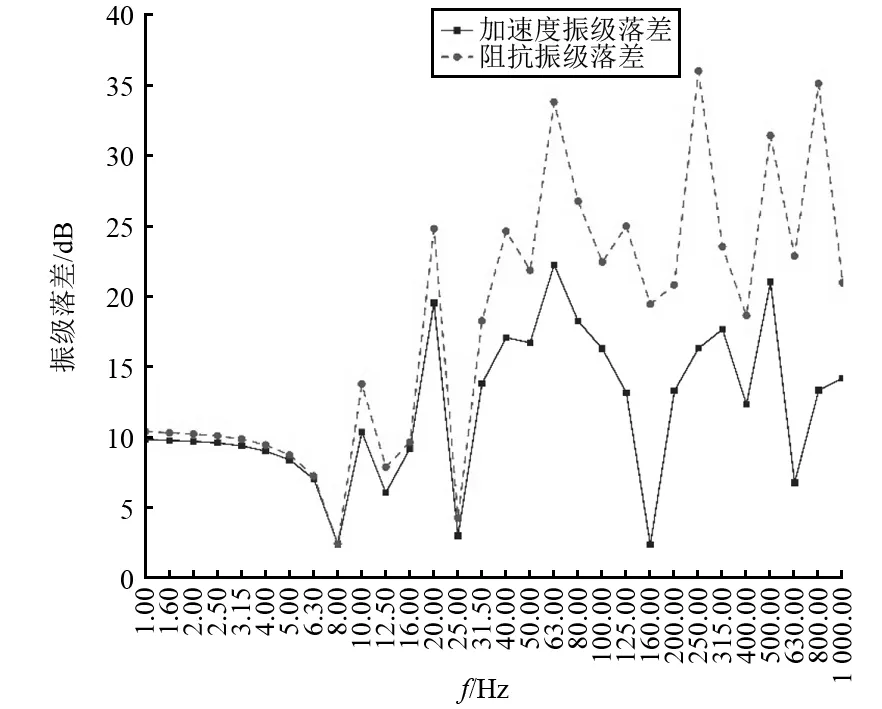
图13 6号位置激励振级落差Fig.13 Vibration level difference of position 6
如图14所示绘制出不同位置激励时各点原点阻抗曲线,如图15所示绘制出不同位置激励时平均传递阻抗曲线,对于舱段基座结构模型,在不同位置激振时不同频率下阻抗曲线十分相似。可以看出,在低频段由于未激励起整体结构振动而使阻抗值偏大,因此评价基座阻抗性能宜取5 Hz以上频率段,综合来看可以取2号位置原点阻抗值来分析基座阻抗性能。
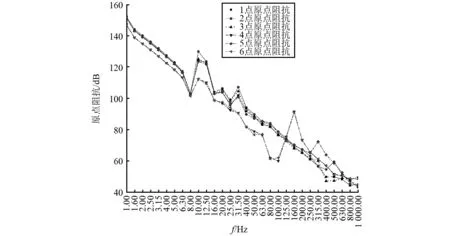
图14 不同位置原点阻抗Fig.14 The origin impedance of different locations

图15 不同位置平均传递阻抗Fig.15 Mean transfer impedance of different locations
4 基于阻抗优化的高传递损失基座设计
4.1 基座设计的阻抗失配、阻抗匹配和高传递损失理论辨析
阻抗匹配是指电路理论中信号源或者传输线与负载之间的搭配方式,当负载阻抗与激励源内部阻抗互相适配,会得到最大功率输出。如果不匹配,则会形成反射,能量传递不过去,降低效率;会在传输线上形成驻波,导致传输线的有效功率容量降低,功率发射不出去,甚至会损坏发射设备。如果是电路板上的高速信号线与负载阻抗不匹配时,会产生震荡,辐射干扰等。阻抗匹配分为低频和高频两种情况。
将该方法推广到基座隔振设计,我们提出基座设计的阻抗失配方法。基座阻抗失配设计的[19]原理是,通过改变基座结构的机械阻抗,使其与外载荷激励源的频谱特性不匹配或错配(即原点阻抗与传递阻抗不匹配),使振动能量或功率输出最小,从而对弹性波具有良好的隔离能力,提高基座的减振性能。
振动阻抗匹配是指结构装置机械阻抗与激励源内部阻抗互相适配(即,原点阻抗与传递阻抗匹配导致振级落差为零),使振动较顺利的传递,减少消耗,改善信噪比,这可以用于利用共振技术的波浪能发电装置设计。
基座高传递损失[20]设计,主要是指通过改变基座结构形式(拓扑或传力路径)和尺寸,附加子系统(质量或刚度)或辅助功能材料(阻尼材料),增大基座的机械阻抗,使基座原点阻抗与传递阻抗失配,使振动传递损失显著增大,达到优良的声学设计目标。根据经验,本文高传递损失定义为具有较大插入损失或阻抗级落差(大于6 dB),或者具有较大阻抗级(例如100 dB)。
4.2 高传递损失基座阻抗优化设计
根据上述理论,本文提出高传递损失基座的阻抗优化设计方法,其数学表达式为
(18)
式中:M,C,K分别为结构质量,阻尼和刚度;Z为结构机械阻抗;IDL,IDL0分别为结构阻抗级落差和阻抗级落差设计值,IDL具体表达式见式(12);ILa1,ILa0分别为基座阻抗级和基座阻抗级优化设计下限值;mass,m1,m2分别为基座系统结构总质量,基座质量下限值和上限值;σ为基座系统结构应力;NE为构件单元总数。
为了验证本文设计方法,对如图16所示的基座结构系统进行方钢阻振[21]优化,方钢采用板单元,以其厚度方向尺寸作为优化参变量。如图17所示,附加方刚进行阻振优化时阻振方钢分三种情况进行布置,分别在腹板中部横向,腹板底部以及基座周围进行布置。基座几何尺寸为:基座面板长度2 000 mm,宽度150 mm,厚度12 mm;基座腹板长度2 000 mm,高度250 mm,厚度8 mm;基座肘板上边长150 mm,肘板下边长300 mm, 厚度8 mm。方钢初始设计尺寸:100 mm×20 mm。基座结构与方钢采用相同钢材,材料密度7 850 kg/m3,弹性模量206 GPa,泊松比0.3。模型四周采用固支约束。
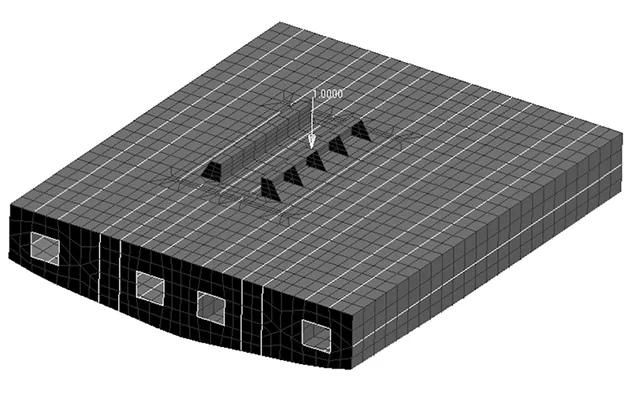
图16 原基座模型Fig.16 Original base model

图17 方钢阻振布置示意Fig.17 Square steel layout
对原基座模型和方钢阻振模型分别进行1/3倍频程频响分析,得到基座阻抗级曲线(见图18),可以看到附加方钢后40~2 000 Hz频率段阻抗级得到提高,优化时选用40~2 000 Hz的总阻抗级作为约束条件。

图18 原基座与方钢阻振模型阻抗级Fig.18 The impedance levels the original pedestal and the square steel model
具体结构优化模型数学表达式为
(19)
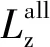
mass=10.048x1+3.14x2+3.14x3
(20)
4.3 板单元模拟方钢验证
本文分别使用梁(Beam)、板壳(Shell)结构单元代替过去有限元计算模型中使用的实体(Solid)单元来模拟方钢的力学性质进行对比分析。
根据文献[22],考虑一个已经在试验中充分测试过的带方钢的实际工程模型,如图19所示。

图19 方钢隔振模型示意图Fig.19 Schematic diagram of square steel vibration isolation model
模型由一块均匀底板与板上的三块方钢组成。均匀面板长3 000 mm,宽1 000 mm,厚8 mm。方钢截面尺寸为100 mm×100 mm,长1 000 mm,分布位置如图1所示。在板面一侧施加20 ~ 8 000 Hz的简谐激振力f,激振力幅值大小为15 N。在底板面按图19所示的分布位置依次选取9个评价点来评价方钢隔振性能。
本文设计了三种不同的模型:单纯板壳模型、三梁与板壳搭配模型、单纯梁模型。使用MSC/Patran建立有限元模型。模型中的板壳部分使用标准Quad4单元模拟,单元大小50 mm×50 mm,梁部分用标准Bar单元模拟,单元长度50 mm。为与实际试验测试数据作对比,设置均匀底板方向对边简支约束。模型材料设置为钢材,质量密度为7 850 kg/m3,弹性模量E= 210 GPa,泊松比v= 0.3。
综合所有上述模型,绘制出各评价点加速度振级落差试验测定值与三种等效模型计算值对比曲线,如图20所示,可以看出使用板单元来模拟方钢能与真实试验测定值更接近,采用板单元来模拟方钢具有可信度。
4.4 阻抗优化模型求解
采用代理模型方法来优化求解,基于Isight平台对样本点建立代理模型,并进一步对近似代理模型优化求解,如图21所示。

图20 振级落差试验测定值与各模型计算值对比图Fig.20 The comparison between the measured values and the calculated values of each model

图21 Isight 集成示意图Fig.21 Integrated sketch of Isight
采用最优拉丁超立方设计方法选点,相比于随机拉丁超立方设计,样本点更加均匀,使得因子和响应的拟合更加真实精确。优先选取设计区域边界上8个点作为样本点以保证边界处拟合误差较小,然后通过最优拉丁超取样方法在设计区域随机选取37个样本点,总共得到45个样本点,在设计区域中的分布如图22所示。为进一步检验代理模型的精度,通过Opt LHD方法随机选取16个样本点作为检验代理模型精度的误差分析测试集。

图22 样本点分布Fig.22 Sample point distribution
为得到精确有效的近似模型,采用三种近似建模方法建立代理模型来对比分析,它们分别是响应面(Response Surface Method, RSM)模型、克里格(Kriging)模型和神经网络((Restricted Boltzmann Machine, RBF)模型。
通过1/3倍频程频响分析得到基座原模型的阻抗级为110.74 dB,选取优化目标阻抗级为116 dB,在优化组件中选用NLPQL优化算法进行分析求解,得到三种近似代理模型优化结果,如表2所示。
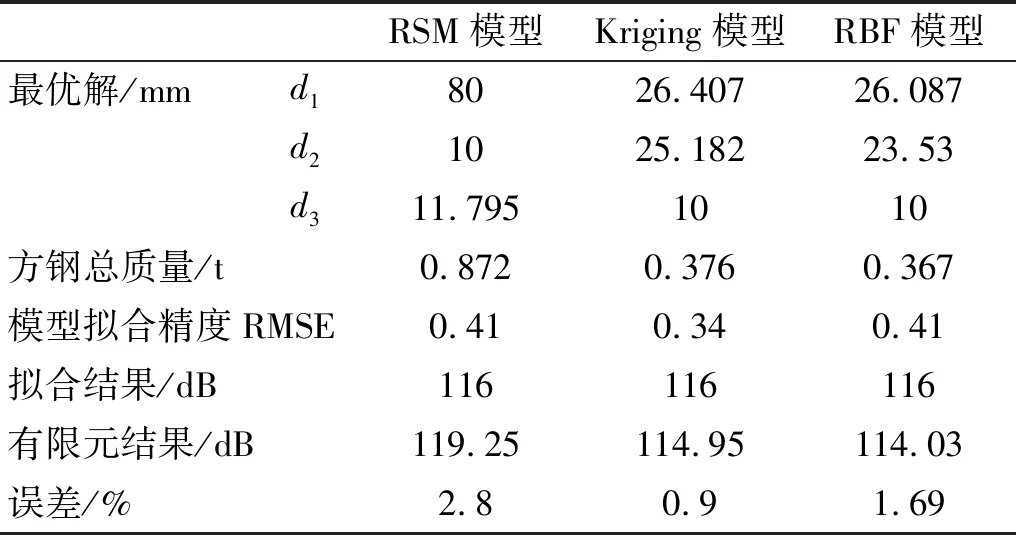
表2 三种近似模型结果对比
从最终的优化计算结果可以看出三种模型都能达到较好的拟合效果,其中克里格(Kriging)模型和神经网络(RBF)模型能更好的反映真实情况,拟合效果也更好。同时,Kriging代理模型和RBF代理模型的最优解十分接近,说明本文的高传递损失基座阻抗优化设计方法是有效可行的。
5 结 论
本文研究了舰艇基于阻抗优化的高传递损失基座设计法,基于阻抗级和阻抗级落差描述基座的减振效果,通过阻抗综合优化设计获得高传递损失基座。研究表明:
(1)利用阻抗级的概念可以较为准确地描述结构减振效果。
(2)高传递损失基座阻抗优化设计是可行的,能实现多参数方钢阻振优化分析。基于Isight平台的近似代理模型优化方法具有较高精度,能提高计算效率,计算结果满足实际工程要求。
(3)工程应用中,综合考虑采用方钢阻振技术时,为达到较好的减振效果,方钢放置在基座周围和腹板与板架相接的位置能有效提高基座阻抗从而提升结构减振性能,并能更大程度节省材料。
