顾及邻近五点的建筑物多边形化简方法
2019-04-03李俐俐李成名卢小平武鹏达
李俐俐,李成名,卢小平,殷 勇,武鹏达
(1. 河南理工大学矿山空间信息技术国家测绘局重点实验室,河南 焦作 454003;2. 中国测绘科学研究院,北京 100830)
建筑物作为地图三大要素之一,在大比例尺地形图的数值载负量和面积载负量中均占有很大比重,对其综合的结果直接影响着地图质量及图面效果[1]。对地图进行缩编时,建筑物多边形综合过程中选择对制图有用的信息进行保留,不需要的信息则舍掉,化简是不可缺少的一步[2]。化简意味着在基本保持其形态特征和面积大小的同时,通过减少其轮廓线的冗余细节,使得建筑物得到更简洁有效的表达[3]。
建筑物化简现已积累了大量的算法,包括垂距法、偏角法和经典的Douglas-Peucker算法、Lang算法[4-6]等。但这些算法只针对线状要素,对于建筑物几何特征的保持没有作过多的考虑。由于建筑物轮廓普遍呈现直角转折形式,因此通用的曲线化简算法无法有效地处理建筑物化简[7]。文献[8]提出了基于邻近四点法的建筑物多边形化简方法。文献[9]改进了邻近四点法,通过对凹凸部类型判别及区别处理实现快速化简,但是化简过于注重面积均衡,导致特征点丢失。文献[10—11]提出了模板匹配方法,用匹配成功的模板来置换原要素实现化简,该方法在匹配中存在多个最相似的模板,不能处理结构复杂的街区,模板库的完备性也有待补充和丰富。文献[12]研究了平面图形的矩形差分化简方法,对规则建筑物的边界化简比较明显,但是并不具有普适性。建立三角网进行全局控制,再对凹凸部位进行填充、删除操作,需要对所有特征点进行三角剖分再对三角形逐一判别、处理,复杂度较高。文献[14—15]研究了居民地的综合策略,包括街区多边形的化简、直角化及夸大等操作的算子设计,并给出了街区综合的一个可行的操作流程。
本文在研究上述算法的基础上,对传统的基于三点、四点的化简算法进行拓展和改善,提出基于邻近五点的建筑物多边形化简算法。该算法通过对多边形凹凸结构的类型判别,判断各类型最小可视长度两边图形的面积,判断弯曲部分是否化简,增加线间的位置关系判定,对不同类型处理单元进行渐进式分类化简。
1 邻近五点组合的定义与结构识别
本文对建筑物多边形邻近的五个节点进行识别,通过邻近四点组成的三边进行处理单元判断,第四条边进行角度判断。本文对于邻近五点的处理可等同于对邻近四边的处理,对于边数小于5的建筑物多边形不作化简。
处理单元组合:本文采用从局部到整体的渐进式处理方法对建筑物进行化简,从最短边开始搜索识别处理单元。将最短边编号设置为L1,两邻边分别编号为L2、L3,其中较短的为L2,另一边为L3,与L2另一边相连接的边设为L4;L1、L2、L3、L4,即1、2、3、4、5点构成一个处理单元组合,结构如图1所示。
Z形、U形定义:算法采用填凹部或削凸部处理手段实现化简,而凹凸部形态至少要四个邻近点才能描述,以多边形上相邻四点作为基本处理单元,将其分成U形和Z形。若1、4位于线段2、3两侧,则将该组合结构称为Z形结构,如图1中的1、2、3、4点组成Z形;否则为U形结构,8、9、10、11点组成U形。在这里,对于U形结构不作进一步细分,仅依据该形态特征对建筑物边界节点进行划分。
平行与非平行模式定义:在实际地图上建筑物并非都是直角形态,会出现各种复杂形态,为进一步化简作准备,需在区分U形和Z形后依据L2和L3位置区分平行与非平行。L2和L3延长后无交点称为平行模式;L2和L3延长后形成交点称为非平行模式。
L3与L4位置定义:对于邻近五点中第四条边在本文接下来的研究过程中,涉及该夹角的角度需判定是否为尖角,因此对其位置进行定义,即以线段L3为基准,沿逆时针方向,L3与L4形成的夹角角度。
2 基于邻近五点的建筑物多边形化简
2.1 化简原理
基于邻近五点建筑物多边形化简方法的思想是通过邻近的五点,根据不同的处理单元组合,依据相应模式对建筑物边界用延伸或缩进两边填充或删除面积小于阈值部分的凹凸部,实行渐进式分类化简。如图2所示。
2.1.1 Z形平行模式
如图2(a)所示,将节点4向长边L3的延长线作垂线,垂足点为点6,同时为最大程度上减小特征点变化,同时使得图形在某一边能保持该边的趋势,对L3和L4进行延伸,交点为点7,判断垂足点6与交点7距离是否在给定阈值范围内,同时加上四边形2347面积判断,若该四边形面积在阈值内,则直接用点7代替垂足点6,删除掉旧节点2、4,则17、75即为化简后的边;若不在,则该边不作化简。
2.1.2 U形平行模式
化简方法同Z形平行模式,此处不再赘述,如图2(b)所示。
2.1.3 Z形非平行模式
算法尽可能保持面积变化最小,选取删减或填充面积较小的部分。此时需要比较L1、L3和L2相交所围成的三角形的面积和L1、L2、L3、L4围成图形的面积大小(如图2(c)所示),选取面积较小的部分进行填充或删除。若三角形面积小,将L1与L3求交点8,18、84、45则为化简后的边。若L1、L2、L3、L4围成图形2347的面积小,此时化简方法同平行模式。
2.1.4 U形非平行模式
对于U形非平行模式,为满足算法尽可能保持面积变化最小,此时需要比较L1、L2和L3相交所围成的三角形的面积和L1、L2、L3、L4围成图形的面积大小(如图2(d)所示),选取面积较小的部分进行填充或删除。若三角形面积小,将L1与L3求交点8,18、84、45则为化简后的边。若L1、L2、L3、L4围成图形2347的面积小,此时化简方法同平行模式。
2.2 化简特点
邻近四点法采用面积均衡处理模式化简,详细见文献[8],化简结果用灰线表示,邻近五点法采用填充或削减模式化简,结果用黑线表示(如图3所示)。从最终化简对比图中可直观看出,邻近五点法基本单元化简模式比四点法更能够保持基本形状且与原图形贴合度更高。基于邻近四点的化简算法过于注重面积均衡,化简时不能顾及更多局部信息,如图3中1、2、3处。
3 建筑物多边形削尖处理
3.1 Z形平行模式
在Z形平行模式下,当延伸L3和L4边进行化简时,L3和L4夹角位置在0~60°和300°~360°之间认为是产生尖角,如图4(a)、图4(b)所示。化简时若在0~60°范围内,连接2、4,删除点3,此时1245即化简后的边(如图4(a)所示)。夹角角度若在300°~360°范围内,此时将点2向L4作垂线交于点7,1275即化简后的边(如图4(b)所示)。
3.2 U形平行模式
在U形平行模式下,当L3和L4夹角位置在0~60°和300°~360°时,将L4延长与L3交于点6后,认为该角度为尖角,如图4(c)、图4(d)所示,此时由点4向L3作垂线交于点7,1745或1754为化简后的边(如图4(c)、图4(d)所示)。
3.3 Z形非平行模式
当L2和L3交点位于L2及L2延长线上时,237面积大于L1、L2、L3、L4围起来的部分面积且L3与L4夹角为0~60°和300°~360°时会形成尖角,如图5(a)、图5(b)所示。此时将点2向L4作垂线,交L4于点8,12、28、85即为化简后的边(如图5(a)、图5(b)所示)。
3.4 U形非平行模式
对于U形非平行模式下,一是当L3和L2的夹角过小时,化简相交时产生尖角;二是当L3和L4的夹角过小时,在延伸的过程中也会产生尖角。
(1)L1、L2、L3围成的三角形面积大于L1、L2、L3、L4围成多边形的面积:当L3与L4的夹角为0~60°和300°~360°,将L1边的点3沿L2平移到4点,将L4沿移动后L1的趋势交L3于点8,判断2348的面积是否在阈值范围内,若在,此时1845为一个基本处理单元,如图5(c)所示。若2348面积大于给定阈值,则该边不作处理。若无交点8,此时直接连接1、4点。
(2)L1、L2、L3围成的三角形面积小于L1、L2、L3、L4围成多边形的面积:当L3与L2的夹角小于60°时,延长L3和L2相交于点6,此时形成尖角(如图5(d)所示),则需考虑L4和L3的位置关系进行化简,化简方法同步骤(1)。
4 化简过程
(1) 建筑物轮廓数据预处理,去除冗余点。
(2) 判断边数,若边数n<5,不进行轮廓化简,化简结束;若边数n≥5,转步骤(3)。
(3) 计算建筑物多边形轮廓最短边,设为L1;通过L1,按照上述组合结构定义,找到L2、L3、L4,判断基本处理单元类型。
(4) 多建筑物多边形化简并作化简过程中削尖处理。
(5) 删除旧节点,连接新节点。
(6) 更新节点,计算多边形最短边。
(7) 重复步骤(3)—(6),直至该面状建筑物轮廓均大于化简指标或边数小于5,化简结束。
5 试验与分析
本文以Microsoft Visual Studio 2010作为开发环境,利用中国测绘科学研究院自主研制的WJ-Ⅲ无级地图工作站,对本文方法进行实例验证。选取某地区1∶1万部分建筑物多边形数据作为试验数据,图6(a)为选取较为典型的一组多边形,图6(b)、图6(c)分别为邻近四点法和邻近五点法的化简结果,图6(d)为邻近四点法与邻近五点法化简结果的对比。
从图6中可以得出,在同比例尺、同阈值情况下,采用邻近四点法和邻近五点法化简都可以基本保持建筑物轮廓特征,但在建筑物轮廓细节特征处的保持,从图6(b)、图6(c)中圆圈处可对比看出邻近五点法保持效果更好。图6(b)、图6(c)中轮廓2、8矩形框处,邻近四点法由于化简前削尖,削尖与化简脱离,尖角不容避免;而邻近五点法顾及尖角,削尖与化简结合,避免尖角的产生。从图6(d)可以看出,对比原始建筑物,邻近五点法化简后的结果更加贴合原始建筑物轮廓,保证了化简前后建筑物的整体结构不发生明显变化。而邻近四点法过于注重面积均衡,虽然保持了基本轮廓特征,但丢失掉特征点。
建筑物多边形化简中特征点的提取、基本形状及面积的保持是评定各种算法精度和效率的重要标准[16]。笔者对建筑物化简结果进行了数据统计,见表1。表1中化简方法1为邻近四点法,方法2为邻近五点法。保留特征点数设定为化简后的点与原建筑物轮廓特征点一致或化简后点在原建筑物多边形边上。从表1统计结果来看,邻近四点法化简后面积变化率大部分小于邻近五点法,这与邻近四点法注重面积均衡一致;在同比例尺化简情况下,邻近五点法相比四点法,化简力度更优,化简后的建筑物点数多,特征保持较好,保留特征点数多,更加贴合原始建筑物,化简效果更好。
6 结 语
本文提出了一种基于邻近五点的建筑物多边形化简方法,通过对建筑物边界特征进行智能识别和分类,采用渐进式化简方法对建筑物容易产生尖角的部分进行削尖处理。本文方法在保持居民地基本轮廓特征的同时,能够很好地避免尖角的产生,保证了化简前后建筑物的整体结构不发生明显变化,相比于邻近四点法更好地保持了建筑物的特征,更加贴合原始建筑物。但该方法没有注意面积均衡问题,同时角度阈值的不同设定也会影响化简结果。在今后的研究中将进一步探讨在面积均衡的同时如何寻求合适的阈值对建筑物多边形进行化简。
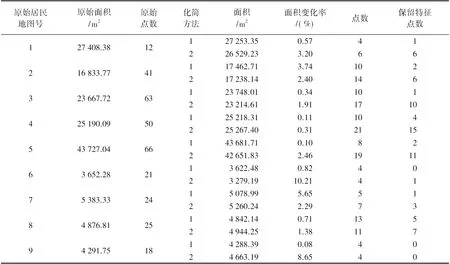
表1 化简试验数据
注:表中各变化率是指化简前后的差值与原始值的比率。
