高分二号卫星影像自适应模糊阈值法小波去噪
2019-04-03张宇航杨武年任金铜邓晓宇
张宇航,杨武年,任金铜,2,邓晓宇
(1. 成都理工大学国土资源部地学空间信息技术重点实验室,四川 成都 610059; 2. 贵州工程应用技术学院贵州省教育厅生物资源开发与生态修复特色重点实验室,贵州 毕节 551700)
高分二号卫星(GF-2)是由我国自主研制的高空间分辨率、高定位精度、快速姿态机动的民用高分遥感卫星。它的成功发射并运行使用,标志着我国在亚米级遥感影像数据取得重大突破[1]。数字图像包括遥感影像,在数据传输保存过程中,受到外界环境的干扰和成像仪器本身的影响,所产生的影像会存在噪声。周期性条纹、亮线及斑点等是常见的遥感影像噪声存在的方式,噪声产生的原因可能存在于如传感器的周期性偏移,或者载荷元器件间的电磁干扰等。噪声的存在降低了图像的质量,严重的会屏蔽需要的辐射信息。针对高分二号高分辨率影像去噪方面研究较少,社会经济价值巨大,使用将会更为广泛的特点,本文采用一种自适应模糊阈值法去噪,进一步提升去噪效果。
图像去噪可分为空间域和频率去噪,空间域去噪常用的方法有均值滤波、高斯平滑滤波、中值滤波等方法[2-3]。1989年,Mallat提出的多分辨分析概念从空间上说明了小波的多分辨率特性,并提出了在多分辨分析基础上发展的快速小波算法,即Mallat算法,这一算法的提出成为小波理论发展的标志性成果[4]。1995年Donoho提出小波硬阈值(hard-thresholding)和软阈值(soft-thresholding)去噪方法,但是硬阈值方法会出现振铃、伪吉布斯效应等视觉失真;软阈值处理方法可能会造成边缘模糊等[5]。2001年Donoho提出了改进阈值算法,Shark L K等提出最优点阈值消噪法,但这些算法中重构信号与真实信号之间总存在一个恒定的偏差,而且当噪声中含有脉冲噪声和高斯噪声混合噪声时,去噪效果并不理想[5]。后续又有文献记载利用隐马尔可夫模型也达到了去噪效果[6]。
1 小波去噪
把图像看作一个二维数据,对其做小波处理。二维小波变换可定义为
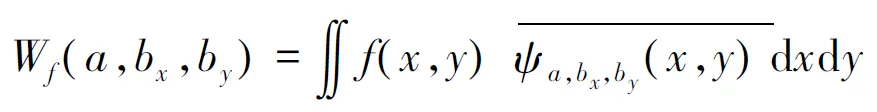
(1)
式中,bx、by为两个维度上的平移[7]。
对应的二维小波逆变换为
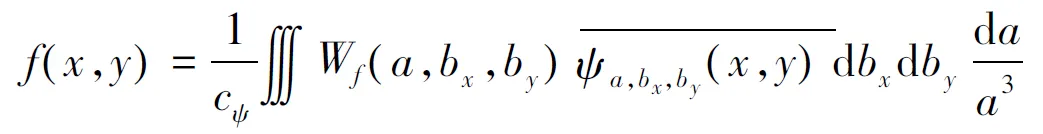
(2)
其中
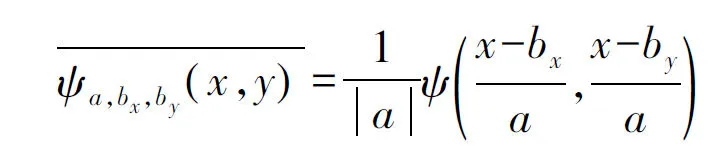
(3)
通过小波变换得到小波系数作阈值处理后,再做小波逆变换,可得到处理后的图像也即人眼识别的直观图像[8]。

(4)
式中,M和α为经验系数,α>1;J为总的分解层数;j为当前分解层数。缺省情况下M取第一层分解后的系数长度L1,一般情况下,M满足L1≤M≤2L1。α的取值根据不同用途选择,压缩情况下一般取α=1.5,降噪一般取α=3。
Donoho阈值处理分为硬阈值和软阈值处理方式[10]

(5)

(6)
2 自适应模糊阈值法去噪
不难发现,Donoho阈值处理方式方便快捷,在实际中也能够广泛便捷地使用,但是该方法存在以下不足[11]:①Donoho阈值获取方式采用默认阈值方式,对于不同尺度下的小波系数的长度是不一样的,但是均采用一个不随尺度变化的阈值,随着分解尺度的增加,小尺度上的边缘细节小波系数一般很小,在滤除噪声时往往同时滤除了部分边缘细节,造成了边缘模糊。②在阈值处理方式上也存在可以改进的地方,从式(5)、式(6)可以看出,硬阈值的处理方式是小波系数在阈值λ附近不连续,产生跳跃点,而软处理方式得到的小波系数整体连续性较好,从而使估计信号不会产生附加震荡,但是会损失图像部分高频信息。针对以上不足,可以采用一种处理方式既简单又能结合以上两种处理方式各自优势的自适应模糊阈值去噪法。其去噪流程如图1所示。
具体说明如下:
(1) 对含噪图像先做中值滤波处理。
(2) 将做过中值滤波预处理后的图像再进一步做小波分解,得到各个尺度下的小波系数。
(3) 根据各个小波系数建立该尺度下的自适应阈值和阈值处理函数。
(4) 经由小波逆变换,得到去噪后的图像。
遥感影像在传感器发射接收信号时,一般都会受到电磁脉冲的干扰。研究发现,一般一幅图像都会存在高斯噪声和脉冲噪声,而中值滤波能够有效消除脉冲噪声的干扰,同时保证边缘细节部分不会丢失[12]。下面给出自适应模糊阈值函数
(7)
(8)
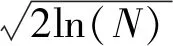

(9)
式中,HH为对角方向的一级高频系数。
3 试验数据结果及结论
本次试验选取四川省隆昌县某区域内GF-2卫星遥感图像。需要说明的是,去噪处理本来是不需要另外加噪的,但此次试验对原始图像加噪,是为了与原始图像对比,尽可能地模拟出传感器接收保存信号过程中会污染图像的复杂混合噪声,在噪声较多的情况下才能更直观地表现出不同方法的去噪效果,因此加入椒盐噪声、高斯噪声和随机噪声。
图2(a)为原始图像,图2(b)为含噪图像。图2(c)—(e)分别为均值滤波、高斯平滑滤波、中值滤波。这几种方法简单便捷,均取得了一定的效果,处理后的效果差别不是很大,其中中值滤波相比其他两种方法效果更优,但以上方法图像细节保留均不是很完好。图2(f)—(j)为不同小波去噪方法下的试验结果图,依次为默认软阈值法、默认硬阈值法、Birge-Massart软阈值法、Birge-Massart硬阈值法、自适应模糊阈值法。硬阈值法处理的图像细节较为明显,软阈值法处理的图像整体较为连贯平滑。
为了量化去噪效果,常用图像的均方误差(MSE)、峰值信噪比[15](PSNR)和改善信噪比[16](ISNR)3个指标来衡量去噪效果。各指标计算公式为
(10)
(11)
(12)
图像的高度和宽度分别用M、N表示;A(i,j)、f(i,j)、g(i,j)分别为原始图像、含噪图像、去噪图像。

表1 不同去噪方法下的各指标值
4 结论与讨论
对于GF-2影像,小波去噪法要优于空间域去噪的3种方法,在空间域去噪方法中,中值滤波取得了较好的效果,PSNR值相比均值滤波高出0.732 8。Birge-Massar阈值法整体效果不如全局阈值法,虽然采取分层阈值处理的方式,但是这种方式在保留图像整体信息完整性和连贯性方面不如全局阈值去噪方式,加之采用单一的硬或软阈值处理方式,因此取得去噪效果不是很理想。小波去噪的不同方法中,硬阈值处理较软阈值处理方式的各指标值更优。本文采用的自适应模糊阈值法,充分结合了硬阈值和软阈值处理方式的优点,根据每层小波系数调整阈值,在以上所有方法中去噪效果最佳,ISNR值相比其他小波去噪方法分别提高了2.5%、11.4%、85.5%、23.8%,取得了更好的去噪效果。
