基于地面图像的卫星自主定轨方法可观测性及定轨性能分析

高有涛，李木子，孙 俊

(1. 南京航空航天大学 航天学院，江苏 南京 210016； 2. 上海航天控制技术研究所，上海 201109)

0 引言

现有的轨道确定技术主要依靠地基观测设备和卫星导航星座。随着对卫星自主性和在轨生存能力需求的不断提升，各类自主导航理论得到越来越多的重视。其中，基于地面遥感图像的自主定轨方法具备以下特点：1)光学遥感卫星本身携带有光学相机，可直接用以定轨，节省载荷空间；2)具有很好的延展性，对于搭载其他波段探测器的卫星同样适用；3)图像中包含丰富信息，借助已有的视觉位姿估计算法，可设计更加灵活多样的定轨方案。

利用地面景物图像进行卫星定轨的思路最早源自20世纪60年代美国空军提出的基于地标的卫星定轨方案[1]。随后，麻省理工学院(MIT)、美国国家航空航天局(NASA)等机构的研究团队分别提出了基于地面遥感图像数据的定轨方案，并进行了可行性分析[2-4]。近年来，相关研究主要是评估使用不同类型地标图像方案的定轨表现[5-7]。

定轨系统的关键问题之一是分析系统的可观测性。只有系统的状态量根据观测可以唯一确定，系统才是可观测的。可观测性的概念最早是由Kalman为解决确定线性系统问题时引入的，用以描述系统利用有限观测确定系统状态的能力。对于航天器精密定轨系统，可观测性是指系统利用有限观测确定航天器轨道状态量的能力。在有关自主导航系统可观测性的研究中，崔平远等[8]针对深空导航系统，讨论了利用太阳视线矢量、地球视线矢量、相对太阳的径向速度及其相互组合作为观测量时系统的可观测性能，得出多种观测量组合下定轨可观测性能最佳，同时还证明了定轨可观测度越高，则定轨精度越高。宁晓琳等[9]分别利用星光角距和星光仰角两类观测量时系统的可观测性，通过比较2种情形下的可观测度，得出利用星光仰角可以得到更高的导航精度的结论。除此之外，一些学者针对测角、磁强计测量等观测量对可观测性进行了分析[10-11]。

本文首先介绍了基于地面遥感图像定轨的基本原理及相关理论模型。随后针对该定轨系统，给出系统可观测性和可观测度的分析方法。最后，通过算例证明了系统的可观测性，对可观测度进行评估，通过仿真实验分析了该定轨系统的定轨精度。

1 基于地面遥感图像的卫星自主定轨原理

地表存在大量可识别的自然或人造特征景物。当对地成像的遥感卫星拍摄地面图像时,可以将这些图像与事先存储在卫星上的特征景物库进行匹配，由此建立实际景物坐标与其像点坐标一一对应的关系。根据该对应关系便可以建立定轨观测模型，从而确定卫星轨道。下面对基于地面遥感图像的卫星自主定轨系统中涉及的轨道动力学模型、观测模型和滤波算法分别进行介绍。

1.1 定轨观测模型

对于理想的pin-hole相机模型，成像过程遵循中心投影透视原理。选取J2000地心天球坐标系作为物方坐标系，在该坐标系中表示地面特征点。成像的几何关系如图1所示。图中：S为投影中心；O为光轴与成像平面的交点；P(xg,yg,zg)为地面特征点；p(u,v,-f)为地面特征点在焦平面上的像点。

图1 测量几何示意Fig.1 Schematic diagram of measurement geometry

像点坐标在像空间坐标系下表示为

(1)

式中：f为相机焦距；(u，v)为焦平面像点坐标。为了建立像点与地面特征点之间的关系，应建立1个辅助坐标系。该坐标系各轴与物方坐标系各轴平行，原点为投影中心。由此可得到在该辅助坐标系下的像点坐标，即

(2)

式中：TA为卫星体坐标系向物方坐标系的旋转矩阵；TI为相机的安装矩阵。辅助坐标系与物方坐标系坐标轴平行，因此根据简单的相似三角形对应边长比一致的原理可得

(3)

式中：(xg,yg,zg)为地面特征点坐标；(x,y,z)为投影中心坐标，近似等于卫星位置坐标。将式(3)代入式(2)便能建立起地面控制点坐标、对应像点坐标和投影中心坐标之间的关系，即

(4)

式中：(a11,a12,…,a33)是(TATI)-1矩阵元素。

由以上推导可建立定轨观测模型，该观测模型的具体形式为

(5)

式中：焦平面坐标(u,v)为定轨观测量；η为二维测量误差。由式(5)可推导出该观测模型下的测量矩阵

(6)

式中：

h1=

h2=

h3=

h4=

h5=

h6=

1.2 卫星轨道动力学模型

近地卫星的轨道运动问题可理解为受摄二体问题，轨道状态量可表示为卫星在J2000地心天球坐标系下各轴方向上的位置速度分量，即

(7)

其满足运动方程

(8)

式中：F0为二体引力项；Fε为各种摄动加速度之和。对于地球低轨卫星，地球非球形引力是最主要的摄动源，除此之外，大气阻力、光压摄动、日月等大天体的摄动也是比较显著的摄动因素。当追求更高的模型精度时，还需考虑来自潮汐、后牛顿效应等因素的影响。

1.3 滤波模型

鉴于动力学模型和观测模型所体现出的非线性特性，采用扩展卡尔曼滤波(EKF)算法对轨道状态量进行估计。滤波算法中的待估状态量即为轨道状态量x，根据式(7)，(8)可构造完整的滤波状态方程，即

(9)

其过程噪声w满足谱密度矩阵，即

(10)

基于以上状态方程，滤波流程由时间更新和测量更新两部分组成。在时间更新中，卫星的轨道状态量由时刻tk-1积分至时刻tk，相应的tk时刻的协方差矩阵为

Pk/k-1=φ(t,tk)Pk-1/k-1φT(t,tk)

(11)

式中：φ(t,tk)为状态转移矩阵。借助时间更新得到的先验轨道状态量和协方差矩阵Pk/k-1，可以求解出测量残差yk和滤波增益矩阵Kk，即

yk=ζ-h(x)

(12)

(13)

(14)

对轨道状态量的更新可表示为

(15)

同时对协方差进行更新，即

Pk/k=(I-KkHk)Pk/k-1

(16)

将改正过的状态量和协方差带入到新的滤波循环中，直至所有观测数据处理完毕，即

F=F0+Fε

(17)

2 系统可观测性分析方法

对于航天器定轨系统，可观测性是指系统利用已有的观测量可以唯一地确定航天器的轨道状态的能力[12]。如果系统的状态量可以根据观测唯一地确定，则该系统是可观测的。在实际处理中，往往利用构造可观测性矩阵的方法对系统的可观测性进行分析。

由以上对轨道动力学模型和观测模型的分析可知，本文构建的基于地面遥感图像的定轨系统为非线性时变系统。将该系统进行分段定常简化[13]，通过局部可观测矩阵对系统的可观测性进行分析。局部可观测矩阵可描述为

(18)

式中：φ表示卫星轨道状态转移矩阵。对任意定轨时刻t，若局部可观测矩阵o(t)满秩，即其秩等于系统状态量的维数n，则称系统在t时刻为局部可观测的。如果在整个定轨弧段内，各定轨时刻的局部可观测矩阵均满秩(秩等于n)，那么该定轨系统就是完全可观测的。

通过对局部可观测矩阵秩的求解可判断系统是否可观测，但这种方式无法反映出系统估计性能的好坏。为了评价系统的估计性能，这里引入可观测度的概念。可观测度表征了观测数据对系统状态量变化的敏感程度，其数值大小一定程度上体现了系统对轨道状态估计的精度。本研究中选取局部可观测矩阵的条件数作为可观测度的度量标准。为了求取条件数，需对局部可观测矩阵进行奇异值分解，其表达式为

O=USVT

(19)

式中：U，V分别为维度m×m和n×n的奇异向量矩阵，其中m为观测量维度p与状态量维度n的乘积；S为由奇异值组成的对角矩阵，其维度与O矩阵一致，均为m×n。至此，利用求得的矩阵奇异值，可求取矩阵条件数，即

(20)

式中：σmin，σmax分别代表矩阵O的最小奇异值和最大奇异值。由条件数定义可知，其在数值上必大于等于1，且条件数越大，矩阵越趋向于病态。应用于定轨系统可观测性的分析中，可以理解为条件数越大可观测度越差，条件数越接近于1可观测度越好，定轨性能更优越。

3 可观测性与定轨性能仿真分析

3.1 仿真条件

仿真中使用WorldView-3卫星的轨道参数(见表1)作为标称轨道初始参数。通过仿真合成的方式产生模拟的定轨观测数据。星载光学相机进行星下点成像，相机焦距为13.3 m，视场为1.27°。在生成仿真数据时，判断摄像机视场内是否存在选取的地面特征点。当摄像机的视场内包含地面特征点时，借助地面特征点位坐标、卫星的标称位置和姿态，根据中心投影原理生成仿真中所用到的地面图像数据。仿真中，需要选取合适的地表特定景物作为在轨卫星可拍照获取的有效特征点。这里选取全球海岸线和主要河流作为候选景物，一是因为该类景物分布广泛且密度较高，方便星载相机获得包含该类景物的有效观测图像；二是因为在实际图像处理中，这类景物往往与周围景物差别明显，更容易识别、匹配。

表1 卫星初始轨道参数

为了模拟星上成像条件，还要考虑影响成像的光照约束，包括昼夜光照变化和云层遮挡(概率为50%)。当星下点区域处于背向太阳一侧或云层遮挡时，卫星将无法获取有效地面图像。仿真中，假设每30 s卫星获取1次星下点图像，需要考虑的误差因素见表2。

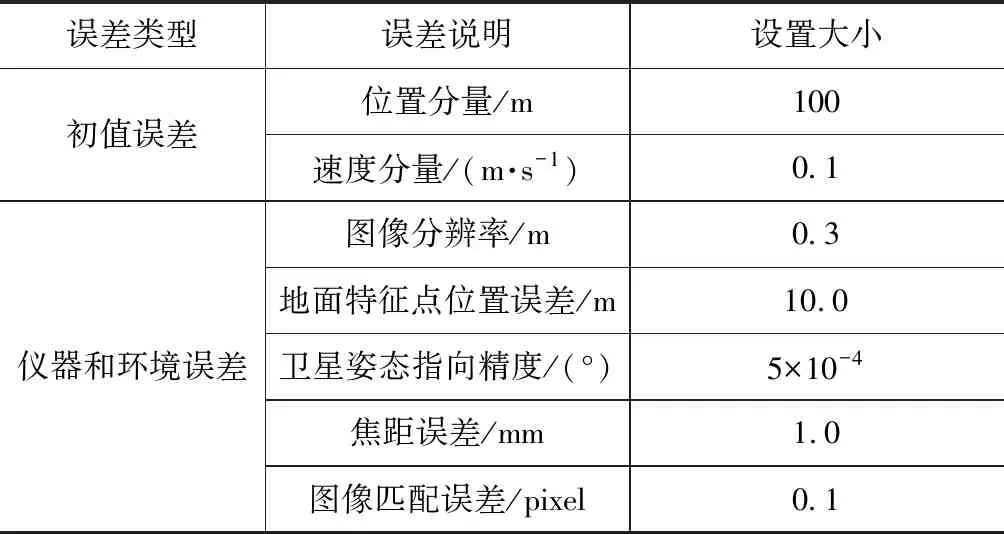
表2 基于地面图像定轨仿真误差参数

3.2 可观测性分析

在以上仿真条件下，对基于地面遥感图像的定轨系统的可观测性进行仿真分析。在2 d的定轨弧段内，实验结果显示：各定轨时刻的局部可观测矩阵的秩均为6，基值等于轨道状态量纬度，这表明各时刻均为局部可观测的，即该系统是完全可观测的。图2展示了可观测度随时间变化的情况，从图中可以看出，除了极少数时刻外，可观测度的值均小于500，整个定轨弧段内可观测度的均值为342.83，这表明该定轨系统可实现对轨道状态量较好的估计。

图2 可观测度随时间变化Fig.2 Variation of observability degree with time

3.3 基于单点的精密定轨与多点定位结果对比

利用Monte-Carlo实验对该系统的定轨性能进行定量分析。图3中展示了2 d的定轨弧段内，各坐标轴方向定轨位置误差、速度误差随时间变化的情况。图中的黑线表示估计得到的轨道与标称轨道间的误差，红线代表由估计协方差矩阵计算得到的3σ误差曲线。从图中可以看出，定轨误差在0.1 d内显著下降达到稳态。这表明在该实验条件下，定轨系统可以实现定轨误差快速收敛。重复进行500次Monte-Carlo实验，得到平均的定轨位置均方根误差为11.74 m，速度均方根误差为1.35 m/s。

上述分析讨论了利用遥感图像中的特征点焦平面坐标为观测量，结合卫星动力学信息的定轨结果。但通过分析式(4)中的成像共线方程可知，当同一幅图像中的特征点数大于等于2时，可以建立至少4个包含卫星位置坐标的独立方程，此时方程个数大于卫星位置坐标维度，因此可利用最小二乘法求解出卫星的位置坐标，称为多点定位方法。

图3 定轨误差随时间变化图Fig.3 Variation of orbit determination error with time

图4 多点定位Monte-Carlo仿真结果Fig.4 Monte-Carlo simulation results of multiple-point position determination

在相同的仿真条件下对2种方法进行比较分析。图4展示了500次Monte-Carlo仿真下多点定位方法卫星位置确定结果，仿真实验中假设每幅图像包含10个特征点。从图中可以发现卫星的定位误差集中在2～150 m的范围内。对多点定位方法和本文提出的定轨方法的定轨结果进行比较，结果见表3。由表可知，使用多点定位方法时，随着控制点数目的增加定位误差逐渐减小。本文提出的定轨方法得到的卫星平均位置均方根误差(RMSE)远小于使用多点定位方法得到的结果。这表明：与多点定位方法相比，本文提出的方法不但能同时估计卫星位置和速度，而且可提供更高的轨道确定精度。

表3 多点定位方法与基于特征点图像精密定轨结果比较

4 结束语

本文构建了一种基于地面特征点图像的卫星自主定轨方法。该方法将在轨获得的光学图像与预存特征点数据库进行匹配，获取地面特征点与焦平面像点的对应关系。通过选取特征点焦平面坐标作为观测量，应用EKF算法实现对卫星轨道状态量的估计。重点对该定轨系统的可观测性进行了讨论。通过构造局部可观测矩阵，证明了该系统完全可观测，且可观测度在102量级，具有较为理想的估计性能。定轨仿真实验同样验证了该方法具有较好的定轨表现，定轨位置精度接近10 m，速度RMSE优于2 m/s。与基于多特征点的多点定位方法相比，该定轨方法可获得更好的定轨表现。由于仿真使用的是合成的观测数据，未包含图像处理的过程，因此无法考虑成像扭曲、相机模型偏差等实际因素对定轨结果的影响。针对这一问题，在后续工作中将利用真实图像数据对该方案进行分析。