地球静止轨道卫星碰撞碎片短期演化风险分析

张海涛，张占月，吴 帅，魏 斌

(1.航天工程大学 研究生院，北京 101416；2.航天工程大学 太空安全研究中心，北京 101416)

0 引言

美国空间监视网2018年6月1日公布的数据显示：地球静止轨道(GEO)区域存在850个可探测的空间目标和大量无法探测到的空间碎片，且有大量空间目标以大椭圆轨道穿越GEO区域。

国外许多机构对空间碎片进行了较为深入的研究，开发的模型包括英国的DAMAGE[2]、西班牙的DELTA[3]、美国国家航空航天局(NASA)的LEGEND[4]、法国的MEDEE[5]、德国布伦瑞克大学的LUCA[6]、英国方位研究局的IDES[7]等。这些模型针对现有的空间环境进行演化分析，采用蒙特卡洛[8]仿真对未来的空间环境进行预估，验证了NASA专家Kessler提出的“凯斯勒现象”[9]。国内许多学者也对空间环境、碰撞风险分析等进行了深入研究，如庞宝君等[10]对空间碎片环境预测算法等进行了研究，白显宗等[11-12]研究了碰撞预警与态势，霍俞蓉等[13]提出了基于拉普拉斯变换的碰撞概率计算方法。以上研究主要是观测当前的空间环境，对空间碎片进行定轨，分析空间碎片对航天器的影响，从而提供预警。

GEO区域存在着大量无法探测到的空间碎片，一旦这些空间碎片与航天器碰撞，就会产生大量新的空间碎片，进一步恶化GEO区域的空间环境[1]，而短时间内人们无法对这些碎片进行定轨。本文运用解体模型仿真解体事件，对新产生的空间碎片与GEO区域现有航天器的碰撞概率进行了计算。

1 空间目标筛选

机构间空间碎片协调委员会(IADC)发布的《空间碎片减缓指南》指出：GEO区域是指海拔高度在(35 786±200) km以内，赤道两侧纬度15°以内的球面约束的环形区域[14]。初始空间目标筛选的目的是通过几何筛选方法，筛选出以近圆轨道运行在GEO环形区域和穿越该环形区域的空间目标，将其作为研究对象。美国空间监视网公布的GEO航天器指的是：轨道周期为0.99～1.01 d，偏心率小于0.01的航天器。截至2018年6月1日，GEO区域的航天器共850个，空间目标总数为16 996个。其中，850个空间目标是以近圆轨道运行在GEO环形区域的空间目标，另外需从总的空间目标中筛选出穿越该环形区域的空间目标。

当且仅当卫星地心距和星下点纬度同时满足以下2个条件时，空间目标运行在或穿越GEO环形区域，即

(1)

δ=arcsin(sini·sin(ω+f))∈(-15°,15°)

(2)

式中：a为轨道半长轴；e为偏心率；i为轨道倾角；ω为近地点幅角；f为真近地点角。空间目标筛选的流程如图1所示。从2018年6月1日公布的16 996个空间目标中，筛选出运行在或穿越GEO区域的1 277个空间目标，其中850个空间目标运行在GEO区域，427个空间目标的轨道穿越GEO区域。

图1 空间目标筛选流程Fig.1 Screening process of space objects

2 基于弦截法的接近分析算法

接近分析是指给定2个空间目标的轨道根数，分析小于给定门限值的起止时间，计算相对距离、相对速度、接近角等信息。在进行接近分析前，为了提高分析效率，需先对空间目标进行筛选，筛选出所有可能发生碰撞的空间目标，筛选出的空间目标即为GEO区域所有可能发生碰撞的空间目标。

接近分析算法分为解析法和数值法。其中：解析法是对空间目标之间的几何关系进行分析，建立解析表达式，通过求导获取空间目标的接近信息，其计算速度快，但对于轨道类型敏感，空间目标的相对距离目前仅针对近圆轨道，在小偏心率假设下存在解析解，无法获得完整的相对运动解析方程。数值法是利用2个空间目标的位置、速度信息，得到两者之间距离随时间的导数，通过求解导数多项式的零点来求解接近时刻和最小距离。相对解析法，数值法编程实现简单，对轨道类型不敏感，但计算时间更长。

在J2000地惯系下，空间目标p和空间目标t之间的距离

(3)

式中：rt，rp为空间目标p，t的位置矢量。相对距离的平方对时间的导数为

(4)

(5)

因此，求解相对距离函数的极小值问题可转换为求解函数L(t)的零点问题。一般的轨道类型无法获得其零点的解析解，运用数值方法可得到满足一定精度要求的数值解。函数求零点的方法有迭代法、牛顿法等[15]。案例仿真中，运用弦截法求解问题。

选取一定时间步长tstep-tstep-1(step≥1)，考虑时间区间(tstep-1,tstep]，当L(tstep-1)<0且L(tstep)>0时，L(t)在该时间区间至少存在1个零点，该零点是2个空间目标距离的极小值点。选取区间的2个端点tstep-1和tstep作为初始迭代值t0和t1，弦截法的迭代式为

(6)

由式(6)可见，当ti+1与ti的差值小于一定误差精度时，迭代结束，ti+1为L(t)在该时间区间的零点，即2个空间目标相对距离的极小值点为接近时刻，此时计算2个空间目标的相对距离，得到相对距离的极小值，该值即为接近距离。

弦截法的收敛阶为1.618，其收敛速度比线性收敛的不动点迭代法快，比牛顿迭代法慢。虽然弦截法比牛顿迭代法收敛速度慢，但其计算过程中不需要对距离求二次导数，即无需求解空间目标的加速度，从而规避了分析空间目标受摄动力这一问题，并降低了不收敛的风险[16]。

对于GEO区域空间目标的接近分析问题，从所研究时间区间的起点开始，选取一定的时间步长，对每一个时间步长区间进行接近分析，可得到接近时刻。时间步长一般取2个空间目标中较小轨道周期的1/5[17-18]，可保证在1个时间步长内，2个空间目标的相对距离只存在1个极小值，且在运用弦截法迭代求解时无法收敛到相对距离的极大值点。

3 轨道演化与近似碰撞概率计算

轨道数据采用TLE两行轨道根数，由于TLE轨道数据是在去除摄动短期项后的平轨道根数，SGP/SDP模型比高精度预报模型HPOP[19-21]预报精度更高，因此本研究进行轨道预报时采用SDP4模型。

目前，国内外对于空间目标碰撞概率的研究已较为成熟，通常分为数值法和解析法。其中，解析法计算速度快，但对轨道类型敏感，仅对特殊轨道在一定假设下存在解析解[22-24]，在仅作短期演化风险分析，不作长期连锁碰撞研究时，进行以下假设：

1) 2个空间目标的位置服从三维高斯分布，且相互独立。

2) 2个空间目标接近持续时间非常短，认为接近期间2个目标的相对运动为线性相对运动，且速度没有不确定性。

3) 2个空间目标的形状为半径已知的球体。

4) 2个空间目标的位置在轨道坐标系RSW下沿3个坐标方向的标准差相等，即2个空间目标的协方差矩阵为

(7)

在假设1～3下，2个空间目标的碰撞概率是2个空间目标半径之和Ra与相对距离r的函数。碰撞概率为

(8)

(9)

4 算例仿真

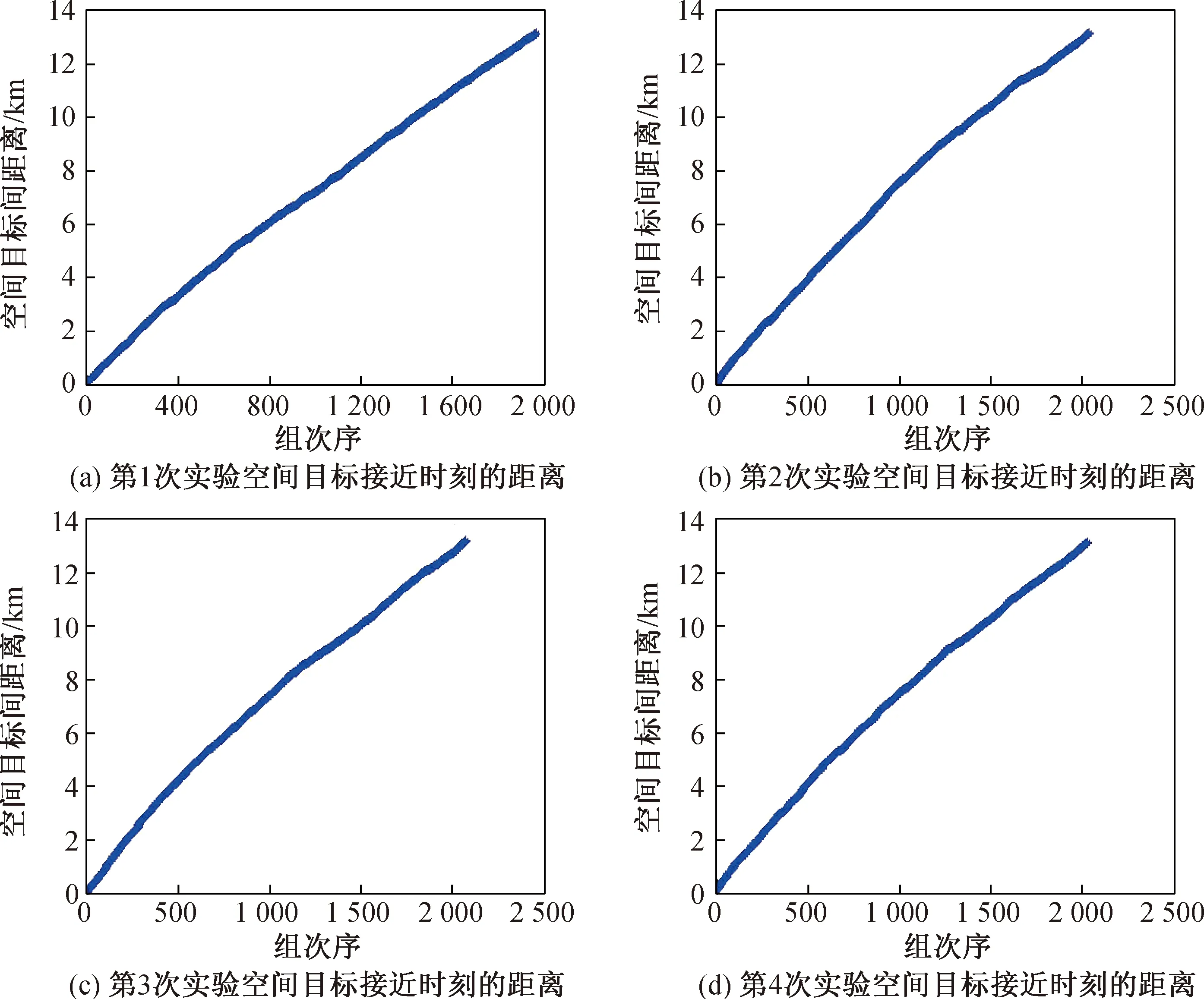
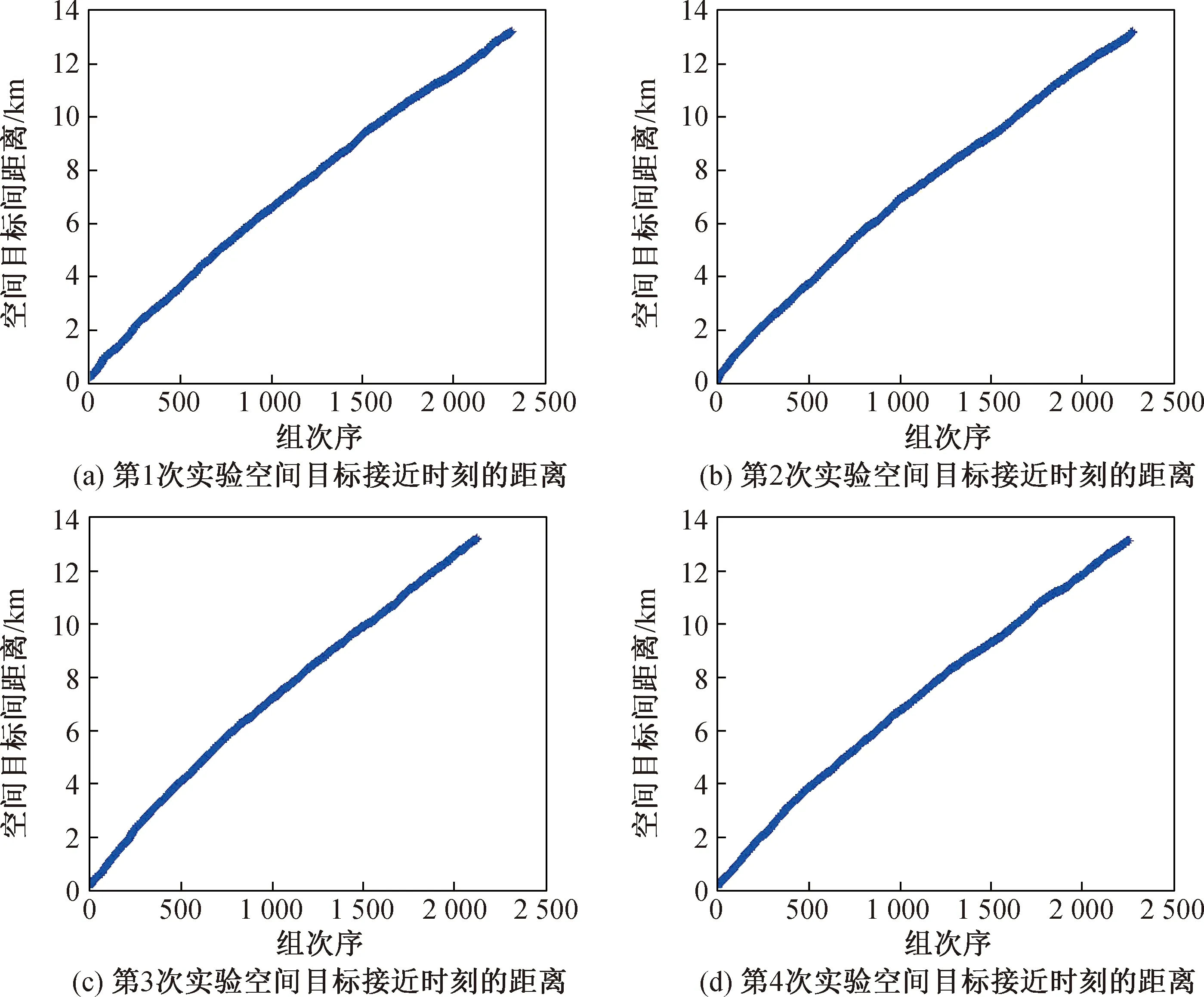
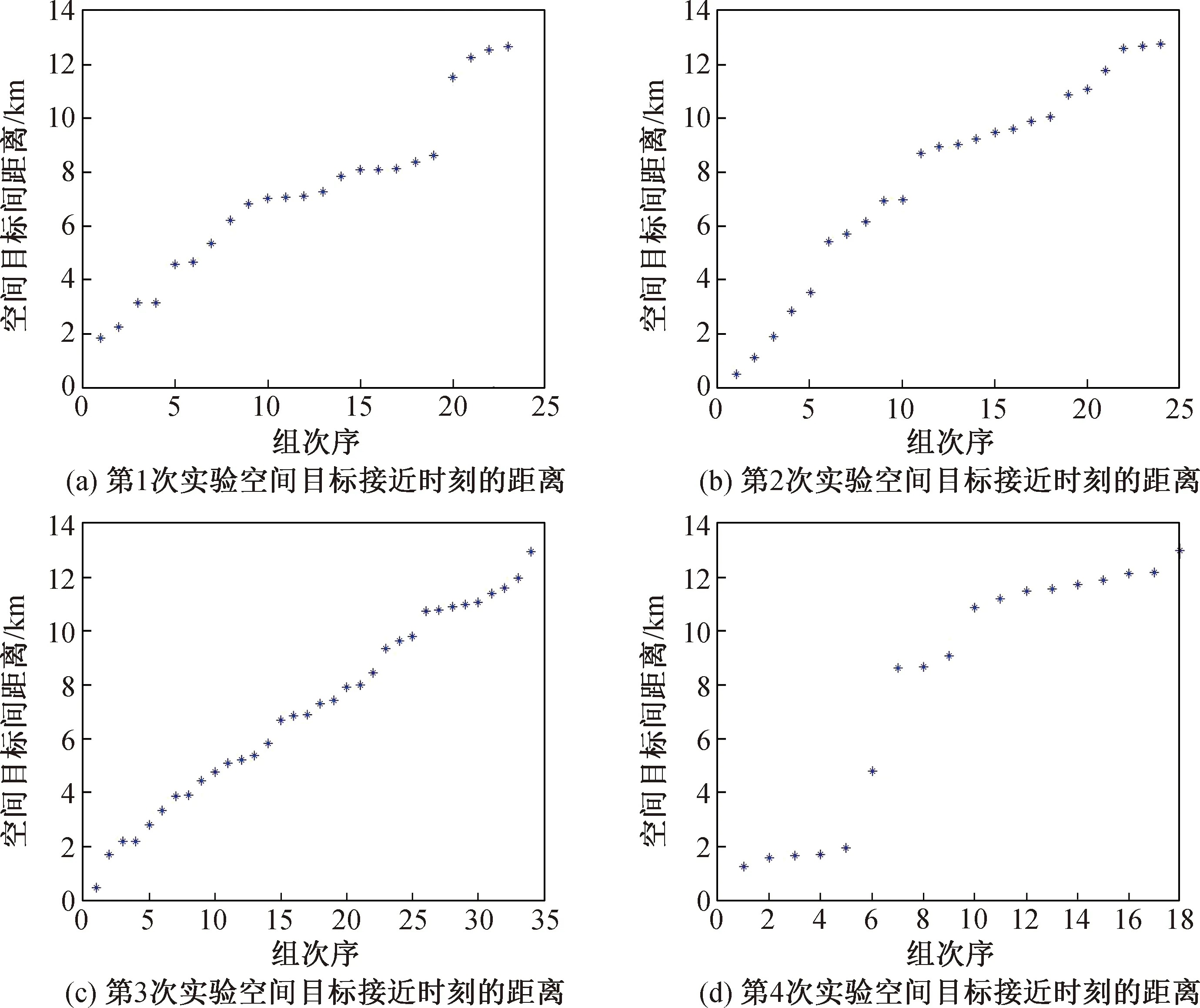
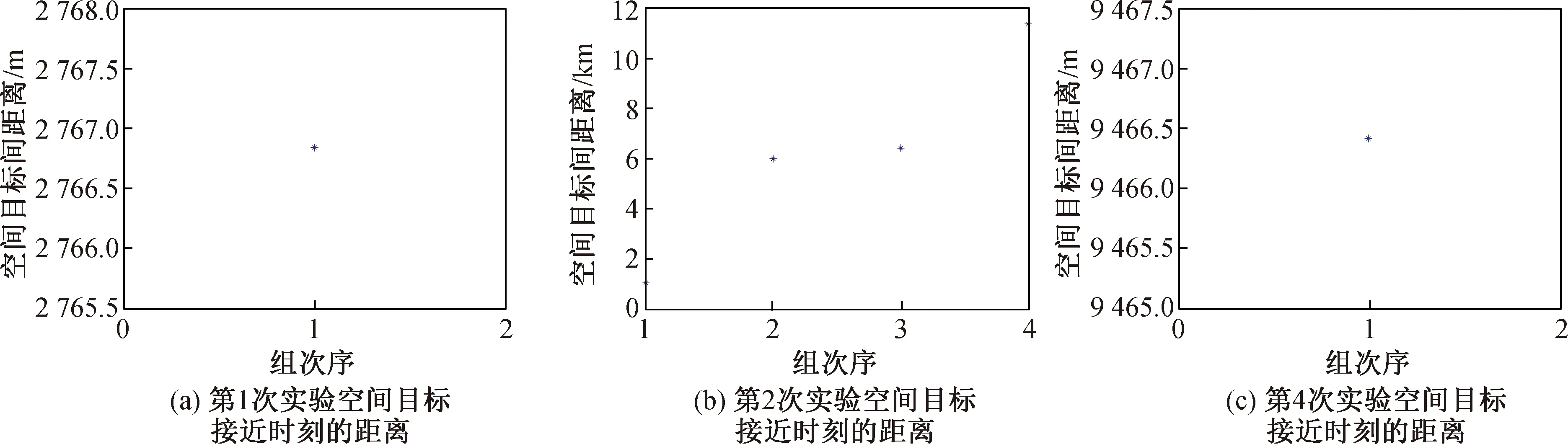
假设实际比能EP=mpv2/(2mt)，临界比能EP*=40 kJ/kg，则当EP≥EP*时，碰撞发生完全解体，当EP

解体模型选取NASA标准解体模型，并考虑质量守恒和动量守恒对解体模型进行修正[26]。空间碎片质量分别取不同值，使卫星发生完全和非完全解体。假设2个空间目标只在距离的极小值点才可能发生碰撞，2个空间目标距离大于等于20 km时不会发生碰撞，分别就2种来源的碎片与目标卫星发生完全和非完全解体碰撞进行仿真，对每种情形进行4次仿真实验，计算在72 h内最接近的时刻、接近距离、碰撞概率。解体产生的空间碎片用“361060001～361069999”进行编号。

4.1 完全解体仿真

4.1.1 情形1

假设该卫星与来自“闪电”轨道的碎片发生碰撞，碰撞相对速度为2 980.6 m/s，假设碎片的质量为25 kg，碰撞发生完全解体，对该过程进行仿真，2018年6月1日0时，空间碎片开普勒轨道根数见表1。

表1 空间碎片1的轨道根数

分析新产生的空间目标和现有空间目标组成的整体间的碰撞概率，4次仿真实验3 d内分别出现1 972，2 039，2 066和2 030组距离小于20 km的接近。每次仿真实验接近距离最小的2个空间目标的编号、距离最小的时刻、最小距离、碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表2，接近时刻的表示方法参照TLE中时间的记法，即前2位表示年份，后3位数字表示该年按顺序排列的天数，小数部分表示1 d中的小数部分(下同)。

表2 在情形1下所用空间目标间接近分析

对于4次仿真实验，碰撞解体后总的空间目标间最接近时的距离按从小到大排列，如图2所示。从图中可以清晰地看出3 d内空间目标间的最接近距离小于某一值的次数。例如：从图2(a)中可以看出，3 d内有200次空间目标间的最小距离小于2 km，有800次空间目标间的最小距离小于6 km。

图2 在情形1下所有空间目标间的接近距离Fig.2 Distance of closest approach between all space objects in situation 1

由4次仿真实验结果可得：新产生的空间碎片与原有的空间目标分别存在169，201，201和187组小于20 km的接近。每次仿真实验新产生的空间目标与原有空间目标间接近距离最小的2个空间目标的编号、距离最小的时刻、最小距离、碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表3，接近时刻的表示方法参照TLE中时间的记法。

表3 在情形1下空间碎片与原有空间目标碰撞分析

对于4次仿真实验，碰撞解体新产生的空间碎片与原有空间目标最接近时的距离按从小到大排列如图3所示。

图3 在情形1下新产生的空间碎片与原有空间目标的接近距离Fig.3 Distance of closest approach between new debris and original space objects in situation 1

当编号为36106的卫星与来自“闪电”轨道的空间碎片碰撞且完全解体时，4次仿真实验显示(见图2，3)，3 d内分别有1 487，1 512，1 601和1 597次空间目标间最小距离小于10 km的现象发生，其中分别有112，131，142和118次发生在新空间碎片与原有空间目标间，分别有1 375，1 381，1 459和1 279次发生在新产生的空间碎片间。其中，112，131，142和118个原有空间目标在轨正常工作的航天器分别有11，7，9和6个，可见该种情形下新的空间碎片对GEO区域的环境影响十分大。

4.1.2 情形2

假设该卫星与运行在GEO附近的碎片发生碰撞，碰撞相对速度为802.6 m/s，假设碎片的质量为320 kg，碰撞发生完全解体，对该过程进行仿真，2018年6月1日0时，空间碎片开普勒轨道根数见表4。

表4 空间碎片2的轨道根数

分析新产生的空间目标和现有空间目标组成的整体间的碰撞概率。由4次仿真实验可得，3 d内分别出现2 324，2 280，2 125和2 260组距离小于20 km的接近。每次仿真实验接近距离最小的2个空间目标的编号，距离最小时的时刻、最小距离、此时的碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表5，接近时刻的表示方法参照TLE中时间的记法。

表5 在情形2下所用空间目标间碰撞分析

图4 在情形2下所有空间目标间的接近距离Fig.4 Distance of closest approach between all space objects in situation 2

对于4次仿真实验，碰撞解体后总的空间目标间最接近时的距离按从小到大排列，如图4所示。

由图可见：3 d内新产生的空间碎片与原有的空间目标分别存在165，153，167和141组小于20 km的接近。每次仿真实验新产生的空间碎片与原有空间目标间接近距离最小的2个空间目标的编号、距离最小时的时刻、最小距离、此时的碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表6，接近时刻的表示方法参照TLE中时间的记法。

表6 在情形2下空间碎片与原有空间目标碰撞分析

对于4次仿真实验，碰撞解体新产生的空间碎片与原有空间目标最接近时的距离按从小到大排列，如图5所示。

图5 在情形2下新产生的空间碎片与原有空间目标接近距离Fig.5 Distance of closest approach between new debris and original space objects in situation 2

当编号为36106的卫星与GEO区域附近的空间碎片碰撞，完全解体时，4次仿真实验结果显示(见图4，5)，3 d内分别会有1 721，1 700，1 587和1 790次空间目标间的最小距离小于10 km，其中分别有103，112，115和101次发生在新空间碎片与原有空间目标之间，分别有1 618，1 588，1 472和1 689次发生在新产生的空间碎片之间。其中，103，112，115和101个原有空间目标中在轨正常工作的航天器分别有9，7，10和8个。可见该种情形下新的空间碎片对GEO区域环境影响非常大。

4.2 非完全解体仿真

4.2.1 情形3

卫星与来自“闪电”轨道的碎片发生碰撞，碰撞相对速度为2 980.6 m/s，产生的碎片质量为10 kg，碰撞发生非完全解体，2018年6月1日0时，对该过程进行仿真，空间碎片轨道根数见表1。

分析新产生的空间目标和现有空间目标组成的整体间的碰撞概率。由4次仿真实验可见，3 d内分别出现23，24，34和18组距离小于20 km的接近。每次仿真实验接近距离最小的2个空间目标的编号、距离最小时的时刻、最小距离、此时的碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表7，接近时刻的表示方法参照TLE中时间的记法。

表7 在情形3下所用空间目标间碰撞分析

对于4次仿真实验，碰撞解体后总的空间目标间最接近时的距离按从小到大排列，如图6所示。

由图可见：3 d内新产生的空间碎片与原有的空间目标分别存在14，13，17和9组小于20 km的接近。每次仿真实验新产生的空间碎片与原有空间目标间接近距离最小的2个空间目标的编号、距离最小的时刻、最小距离、碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表8，接近时刻的表示方法参照TLE中时间的记法。

表8 在情形3下空间碎片与原有空间目标碰撞分析

对于4次仿真实验，碰撞解体新产生的空间碎片与原有空间目标最接近时的距离按从小到大排列，如图7所示。

图6 在情形3下所有空间目标间的接近距离Fig.6 Distance of closest approach between all space objects in situation 3

当编号为36106的卫星与来自GEO区域附近的空间碎片碰撞且发生非完全解体时，4次仿真实验显示(见图6，7)，3 d内分别会有19，17，25和9次空间目标间的最小距离小于10 km，其中分别有11，8，10和5次发生在新空间碎片与原有空间目标间，分别有8，9，15和4次发生在新产生的空间碎片间。原有空间目标中无在轨正常工作的航天器。该种情形下新的空间碎片对GEO环境影响主要体现在新产生的空间碎片有可能发生2次碰撞，进而产生更多的空间小碎片。

4.2.2 情形4

假设该卫星与运行在GEO区域附近的碎片发生碰撞，碰撞相对速度为802.6 m/s，假设碎片的质量为10 kg，碰撞发生非完全解体，对该过程进行仿真，2018年6月1日0时的空间碎片轨道根数见表4。

分析新产生的空间目标和现有空间目标组成的整体间的碰撞概率。由4次仿真实验可见，3 d内分别出现1，4，0和1组距离小于20 km的接近。每次仿真实验接近距离最小的2个空间目标的编号、距离最小时的时刻、最小距离、此时的碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表9，接近时刻的表示方法参照TLE中时间的记法。

表9 在情形4下所用空间目标间碰撞分析

对于4次仿真实验，碰撞解体后总的空间目标间最接近时的距离按从小到大排列，如图8所示。

图8 情形4所有空间目标间的接近距离Fig.8 Distance of closest approach between all space objects in situation 4

由图可见：3 d内新产生的空间碎片与原有的空间目标分别存在1，3，0和1组小于20 km的接近。每次仿真实验新产生的空间碎片与原有空间目标间接近距离最小的2个空间目标的编号、距离最小时的时刻、最小距离、此时的碰撞概率和每次实验3 d内碰撞次数的期望(所有可能发生碰撞的碰撞概率之和)见表10，接近时刻的表示方法参照TLE中时间的记法。

对于4次仿真实验，碰撞解体新产生的空间碎片与原有空间目标最接近时的距离按从小到大排列，如图9所示。

当编号为36106的卫星与来自GEO区域附近的空间碎片碰撞，非完全解体时，4次仿真实验显示(见图8，9)，3 d内分别会有1，3，0和1次空间目标间的最小距离小于10 km，其中分别有1，2，0和1次发生在新空间碎片与原有空间目标间，分别有0，1，0和0次发生在新产生的空间碎片间，无在轨正常工作的航天器，可见该种情形下新的空间碎片对GEO区域的环境影响相对较小。

表10 在情形4下空间碎片与原有空间目标碰撞分析

图9 在情形4下新产生的空间碎片与原有空间目标接近距离Fig.9 Distance of closest approach between new debris and original space objects in situation 4

5 结束语

来自“闪电”轨道的空间碎片若与GEO卫星发生碰撞，两者相对速度较大，则会产生大量的空间碎片。本文在完全解体情形下开展了4次仿真实验。仿真结果显示，新产生的空间碎片在3 d内会与原有空间目标平均发生189.5次小于20 km的接近，最小接近距离降低到434.32 m。在不完全解体的情形下，4次仿真实验结果显示，新产生的空间碎片在3 d内会与原有空间目标平均发生131.5次小于20 km的接近，最小接近距离降低到214.45 m。因此，来自“闪电”轨道的空间碎片与GEO卫星发生碰撞，无论是否发生完全解体，对GEO区域的影响都非常大。

对于来自GEO区域的空间碎片与GEO卫星发生碰撞的情形，两者相对速度较小，较大质量的空间目标与GEO卫星发生碰撞，才会导致卫星完全解体。在完全解体情形下，4次仿真实验结果显示，新产生的空间碎片在3 d内会与原有空间目标平均发生13.3次小于20 km的接近，最小接近距离降低到1 893.31 m。在不完全解体的情形下，由4次仿真实验可见，新产生的空间碎片在3 d内会与原有空间目标平均发生1.3次小于20 km的接近，最小接近距离降低到2 766.84 m。GEO区域的空间碎片与GEO卫星发生碰撞，当发生完全解体时，对GEO区域影响较大，当发生非完全解体时，对GEO区域影响相对较小。本文给出了GEO卫星碰撞碎片短期风险分析的方法，解决了GEO区域空间目标碰撞短期无地面观测数据的问题。下一步将建立专用于GEO区域空间目标的长期轨道预报半解析模型，改进DAMAGE，LEGEND模型中“Cube”(立方体)碰撞概率计算模型在描述空间目标运动特性方面的不足，分析空间碎片与航天器发生碰撞后空间环境的长期状况。