基于MOEA/D的三锥体拦截器气动外形优化设计
2019-04-03曹粟,蒋锋,李易
曹 粟,蒋 锋,李 易
(1.西北工业大学 航天学院,陕西 西安 710072; 2.陕西省空天飞行器设计重点实验室,陕西 西安 710072; 3.上海航天技术研究院,上海 201109)
0 引言
与传统飞行器相比,高超声速滑翔飞行器突破了常规的弹道再入飞行模式,在再入大气层后能以极高的速度飞行,具有很强的突防能力。因此,未来临近空间防御问题也将愈加突出。通常情况下,为有效拦截临近空间目标,拦截器需获得更高的飞行速度,而再入式飞行是获得较高飞行速度的有效方式。然而,再入式飞行器通常面临速域宽、航程远和飞行环境恶劣的任务特点。在设计时,要考虑拦截过程中的总热流量、飞行时间、航程等问题[1]。因这些指标一般具有冲突性,故需采用多目标优化方法进行设计和研究。
求解多目标问题时,通常将原问题分解为多个单目标子问题。文献[2]基于边界交叉法,对再入轨迹优化问题进行分解和优化。文献[3]提出一种三维流场的乘波体外形快速生成方法,通过调整其前缘曲线,实现飞行器升阻比和容积率的两目标问题求解。本文主要采用基于分解的多目标进化算法(MOEA/D)和标量分解方法,将相互耦合的多目标优化问题转化为单目标问题,从而实现优化[4]。相较于传统的NSGA-Ⅱ等方法,本文方法具有更快的收敛速度,能得到更好的优化结果[5]。
本文首先建立拦截器的气动力、气动热和拦截弹道模型;然后以航程、总热流量和飞行时间作为多目标优化的目标函数,利用基于高斯伪谱法的GPOPS程序[6]对其进行求解;最后利用MOEA/D计算得到Pareto前沿与优化外形。优化结果验证了该方法的有效性。
1 拦截器分析模型的建立
1.1 拦截器几何外形
根据任务时序,三锥体拦截器会呈现2种形态,分别为安装有整流罩的三锥体外形和具有较高升阻比的双锥-尾翼组合体外形。在拦截飞行前段,刚进入并穿越稀薄大气区时,拦截器为三锥体初始形态;在进入稠密大气后,尾锥分离,呈现双锥-尾翼外形,从而为飞行器提供较大升力。
基于参数化建模的思想,为降低建模复杂度并减小计算量,将该三锥体外形参数设定为球头半径RN,3段长度L1,L2,L3,以及3段半径R1,R2,R3。三锥体半径的增加,可有效降低飞行器的热流率,但也会因此而增大飞行器的阻力系数,降低其气动性能。在分离后的双锥-尾翼组合体气动外形设计中,为简化计算,取尾翼前端位置为第3段锥体的中点。上述2种形态的飞行器的外形剖面如图1,2所示。
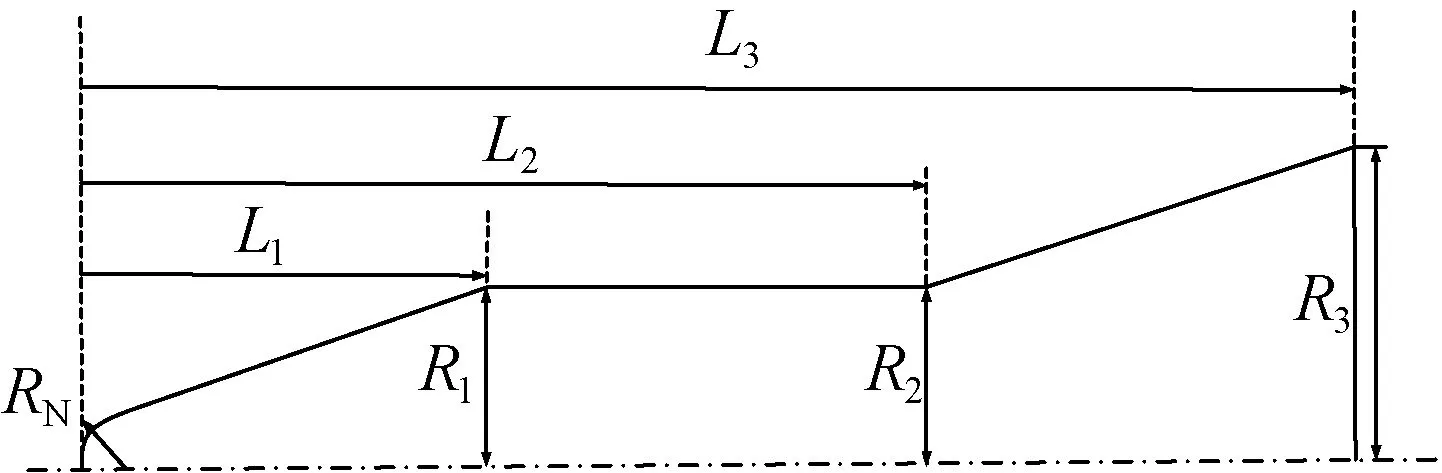
图1 三锥体气动外形剖面Fig.1 Aerodynamic profile of triple-cone interceptor

图2 双锥-尾翼组合体气动外形剖面Fig.2 Aerodynamic profile of combination
1.2 空气动力计算模型与验证
高超声速飞行器的空气动力计算对于确定其气动外形、飞行轨迹和性能极为重要。因当前的风洞试验无法完全模拟高超声速飞行的真实条件,故在概念设计中,需采用快捷有效的工程估算算法。
由于拦截器在飞行中主要处于连续流和自由分子流之间的稀薄过渡流区域,因此可用当地桥函数等加权函数来综合考虑其动力特性。在应用当地桥函数前,需分别确定连续流和自由分子流区域的气动特性。
对于连续流区,采用Dahlem-Buck方法[7]估算物面压力系数,并进行马赫数、背风区的经验修正,计算公式为
(1)
式中:Ccontinue为连续流区压力系数;Ma∞为来流马赫数;θ为来流与物面夹角;K为常数。
对于自由分子流区,通常采用经验公式拟合方法[8],具体采用文献[9]中物面压力系数计算公式
(2)
式中:Crare为自由分子流区压力系数;fn为粘性系数;S为参考面积;TW为物面温度;T∞为来流温度。
在得到飞行器在连续流区的气动系数Ccontinue和非连续流区的气动系数Crare后,利用特定的桥函数方法将两者进行组合,得到稀薄气体过渡流区的气动特性系数
Ctran=PbKn∞Crare+(1-PbKn∞)Ccontinue
(3)
式中:Pb=sin2φ,其中,φ=π(a1+a2lgKn∞),此处,a1,a2为待选系数,Kn∞为来流努森数。
为验证上文介绍的快速估算算法的可靠性,需将其与计算流体动力学(CFD)方法的计算结果进行比较。CFD方法主要包括基于自由分子流理论的直接模拟蒙特卡罗(DSMC)法和基于连续流理论的纳维-斯托克斯(NS)方程法。针对飞行器稀薄效应较为显著的50 km的飞行高度,本文分别采用DSMC法与NS方程法对三锥体外形进行气动计算,并与桥函数工程算法进行比较,结果如图3所示。
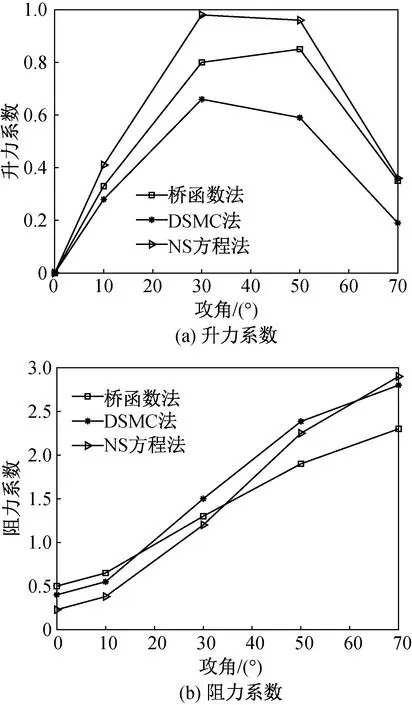
图3 三锥体气动系数计算对比Fig.3 Comparison of aerodynamic coefficients of triple-cone interceptor
由图可知:桥函数法与2种CFD方法的计算结果并无较大差别,升力系数相对误差最大不超过20%,阻力系数相对误差最大不超过10%。两者相对误差最大值均在大攻角处,且在攻角小于30°时相对误差均较小。因此,桥函数法的计算精度符合要求,下文在估算飞行器气动参数时将采用该方法。
1.3 拦截弹道计算模型
不考虑地球旋转,在侧滑角为0的假设条件下,拦截器无动力3自由度质点动力学和运动学方程为
(4)
式中:r为飞行器地心距;θ为经度;φ为纬度;v为飞行器相对地球速度;γ为速度倾角;ψ为速度方位角,ψ=0°表示正东方向;σ为倾斜角;D和L分别为阻力加速度和升力加速度;g为地球重力加速度,g=9.8 m/s2。拦截弹道计算方法采用高斯-伪谱法[10]。
1.4 热流计算模型
采用Fay-Riddle公式估算拦截器的驻点热流,将高温气体边界层偏微分方程转为常微分方程[11]。假设与气体热力学特性、输运特性有关的无因次参数为一系列常数:普朗特数Pr=0.71;路易斯数Le=1.0~2.0;ρsμs/(ρwμw)=1.0,其中,ρs为驻点空气密度,μs为驻点空气粘性系数,ρw为壁面空气密度,μw为壁面空气粘性系数。当飞行速度为1.77~7.00 km/s,飞行高度为7.6~37.0 km,壁温为300~3 000 K时,利用有限差分法,对平衡、非平衡和冻结流进行大量的数值计算。最终,驻点的热流密度qs可表示为
(5)
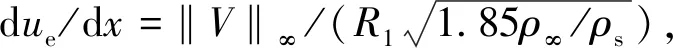
(6)
(7)
式中:Ts为驻点温度。
2 MOEA/D介绍
在此简要介绍MOEA/D的思路和流程。MOEA/D主要将多目标的优化问题分解为多个标量子目标进行优化,然后使用遗传算法求解这些子问题。因相邻两个子问题的优化解非常相似[2],故在MOEA/D中,每个子问题都可使用其相邻子问题的优化信息,从而提高优化效率,减小计算量。其流程如下[12]:
1) 初始化解集与种群。首先,令Pareto解集为∅。然后,计算权重索引集,将其记为B(i)={i1,i1,…,iT},其中,λi1,λi2,…,λiT为距离权重向量λi的欧几里得距离最小的T个向量。之后,建立初始种群x1,x2,…,xN,并设置种群的支配变量Vi=F(xi)。根据具体问题,初始化最优值的解集z=[z1z2…zi]T。
2) 更新解集。从B(i)中随机选择2个下标k和l,利用遗传算法的特点,从xk和xl中产生新解y,然后更新z。对j=1,2,…,m,若zj 3) 若满足循环终止条件,则停止循环。 3.1.1 设计变量 设球头半径为定值30 mm,设计变量为图1中长度变量L1,L2,L3,R1,R2,R3,决策变量x为 x=[L1L2L3R1R2R3]T (8) 3.1.2 优化目标 该飞行器飞行时间长,且要穿越稀薄大气与稠密大气区域,飞行器热环境严峻,这要求拦截器拦截时间尽可能短,并保证拦截范围尽可能大。因此,设置优化目标为最大化航程R、最小化飞行时间t和最小化飞行总热流量Q,并将GPOPS的弹道优化结果作为该气动外形的目标函数值,即 minF=[-RtQ]T (9) 3.1.3 约束条件 过程约束、控制量约束、初始状态量和终端条件设置如下:最大热流密度为1 600 kW/m2;法向过载nz=Lcosα+Dsinα<5;弹道倾角区间为[-5°,5°],末端倾角为0°;攻角区间为[-10°,30°];倾侧角区间为[-70°,70°];始端速度为7 864 m/s,末端速度为1 812 m/s;始端高度为100 km,末端高度为35 km;始端航向角为90°。 飞行器气动外形的设计变量的基准值和上下限见表1。优化初始种群规模为200,最大迭代步数为100,邻近个体的数量为30,不满足约束的惩罚因子为1 000。 表1 外形参数变量取值 图4为优化后的Pareto前沿三维示意图。针对拦截器外形进行单目标优化。单目标优化为多目标优化的一种特殊情况,即在分解目标时将分解向量中的元素λi设为1,其余分量设为0。因此,航程、飞行时间和总热流量单目标优化结果可近似认为是单目标最优解。得到单目标最优解后,代入弹道程序进行计算,可得飞行器的飞行轨迹,结果如图5所示。图中:实线部分为飞行器三锥体形态的轨迹;虚线部分为组合体形态的轨迹。基于该优化结果的飞行器外形如图6所示。图中:虚线部分为飞行器的基准外形。 选择航程作为单目标优化问题,航程最远弹道优化结果如图5(a)所示。图中:实线部分为单目标航程最远的气动外形对应的弹道优化结果;虚线部分为基准外形的最远弹道优化结果。因分离后的两锥-尾翼组合体拥有更大的升阻比,故根据“理想状况下升阻比越高,航程越远”的规律,飞行器分离时间较早。就优化结果而言,其航程高于基准值约17%,总热流量增加15%,飞行时间增加19%。图6(a)为优化后的气动外形与基准外形的对比图。由图可见:优化后的外形长细比更大,飞行器的升阻比等气动性能得到有效提高。 图4 优化后的Pareto前沿示意图Fig.4 Schematic diagram of Pareto frontier after optimization 图5 拦截弹道计算结果Fig.5 Results of intercept trajectory simulation 图6 气动外形优化结果Fig.6 Results of aerodynamic shape optimization 选择飞行时间作为单目标优化问题,飞行时间最短弹道优化结果如图5(b)所示。图中:实线部分为单目标再入时间最短的气动外形对应的弹道优化结果;虚线部分为基准外形的最短飞行时间优化结果。因三锥体形态较分离后双锥-尾翼组合体有更大的阻力系数,故飞行器在绝大多数时候都处于分离前的状态,从而实现速度与高度的快速下降。与基准外形相比,优化后,飞行器航程缩短了7.3%,总热流量减少了35.0%,飞行时间减少了9.9%。基于最短飞行时间的外形优化结果如图6(b)所示。由图可见:优化后的外形底部半径略有增大,阻力系数也因此而有所增大。 选择总热流量为单目标优化问题,总热流量最小弹道优化结果如图5(c)所示。图中:实线部分为单目标总热流量最小的气动外形对应的弹道优化结果;虚线部分为基准外形的最小总热流量优化结果。与图5(b)类似,飞行器直到最后时刻才进行分离。类似地,其航程缩短了9.5%,总吸热量减少了15.4%,飞行时间减少了8.7%。其外形设计结果如图6(c)所示。更钝的头部可有效减小驻点热流密度,从而减轻飞行器的热防护压力。此外,更大的底部半径可增大飞行器的阻力系数,有利于减少飞行器的飞行时间。 通过对比3个单目标的优化结果可知,较大的头部钝度或较长的底部半径可减小飞行器的热流密度,但会降低升阻比,进而缩短飞行器的航程。由此可见,在单目标优化中,飞行时间与总吸热量成正相关关系,但与航程存在冲突,并不存在同时满足每个目标函数均最优的解法,因而需要在多目标优化设计中寻找平衡点。 基于Pareto前沿结果与单目标优化结果,选择一个3目标函数均优于基准值的外形。3目标同时优化的计算结果如图5(d)所示。就优化结果而言,航程增加了12.5%,飞行时间减少了9.5%,总吸热量减少了10.0%。然而,由于尽可能简化了飞行器的几何外形参数,同时在气动数据和飞行气动热的计算中采用了快速估算算法,因此,优化结果在一定程度上存在误差,但仍具一定的参考价值。 本文针对一种可分离的三锥体临近空间拦截器进行了多目标优化。首先,结合基于高斯-伪谱法的弹道计算模型、气动力快速估算算法和气动热计算方法,建立飞行器分析模型。之后,采用MOEA/D计算Pareto前沿,得到3个单目标最优解和一个3目标同时改进的较优解。优化结果表明:该目标优化算法具有一定的参考价值,可为未来的拦截器设计提供参考。由于采用了快速估算算法,计算结果存在一定误差,因此,后续需研究更精确高效的气动模型计算方法,以及MOEA/D在飞行器优化问题上的改进方案。3 拦截器的多目标优化模型
3.1 优化问题设置
3.2 优化变量
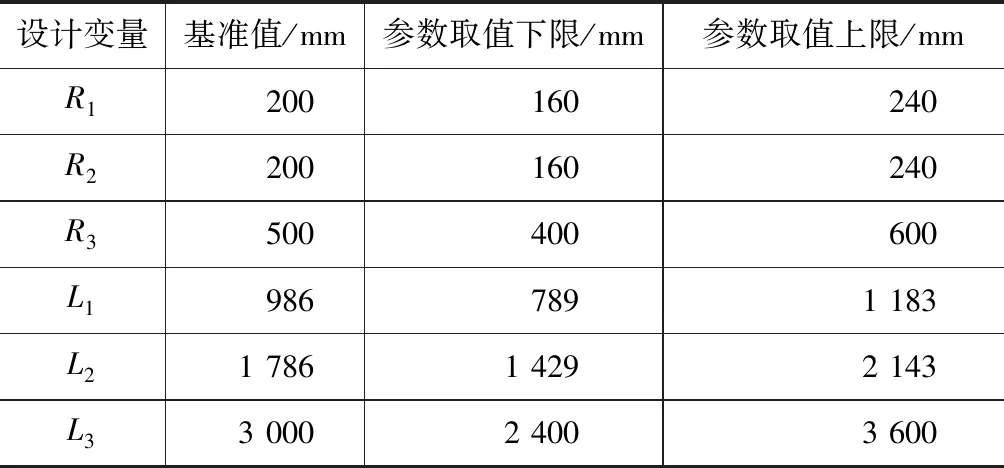
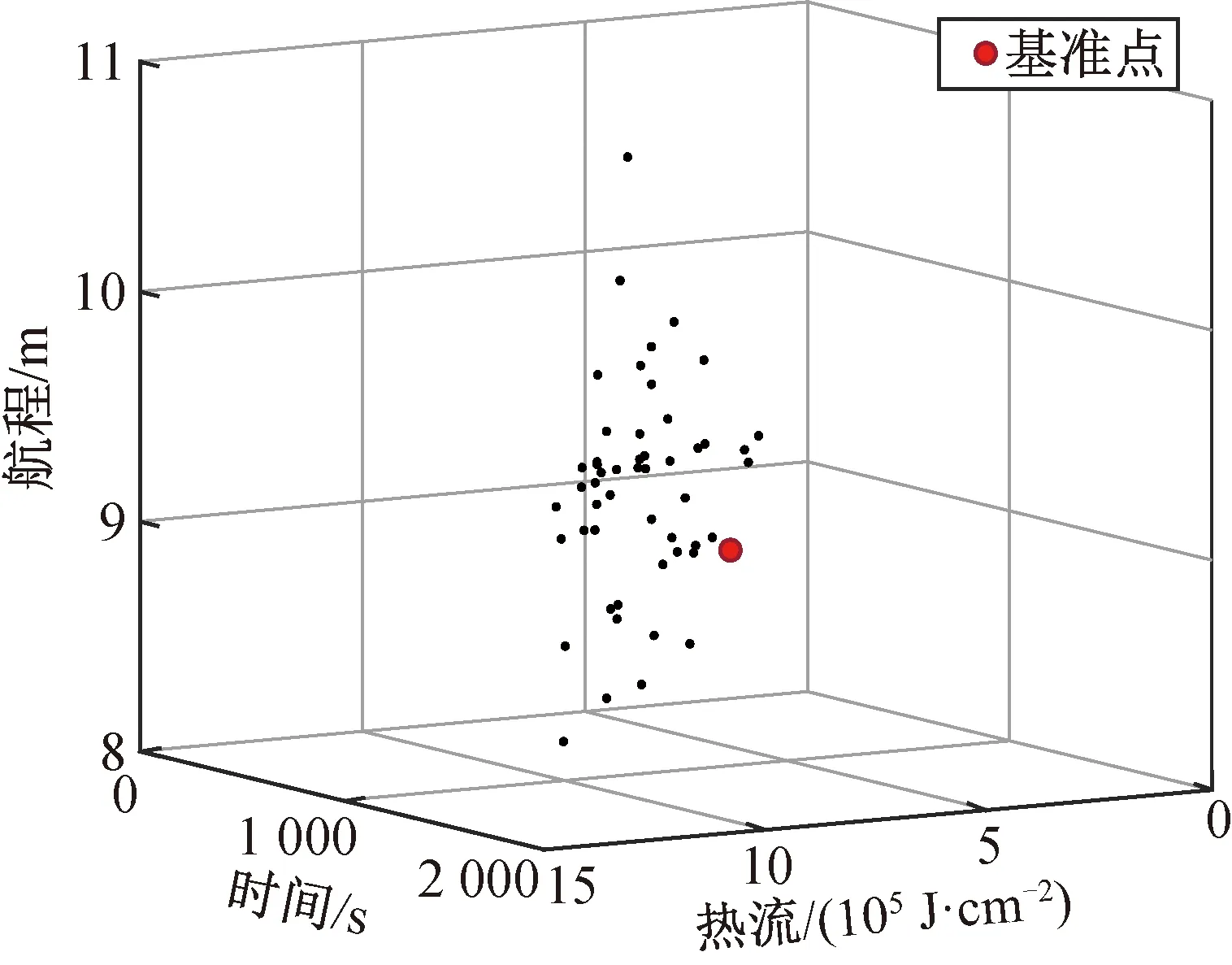
4 仿真结果
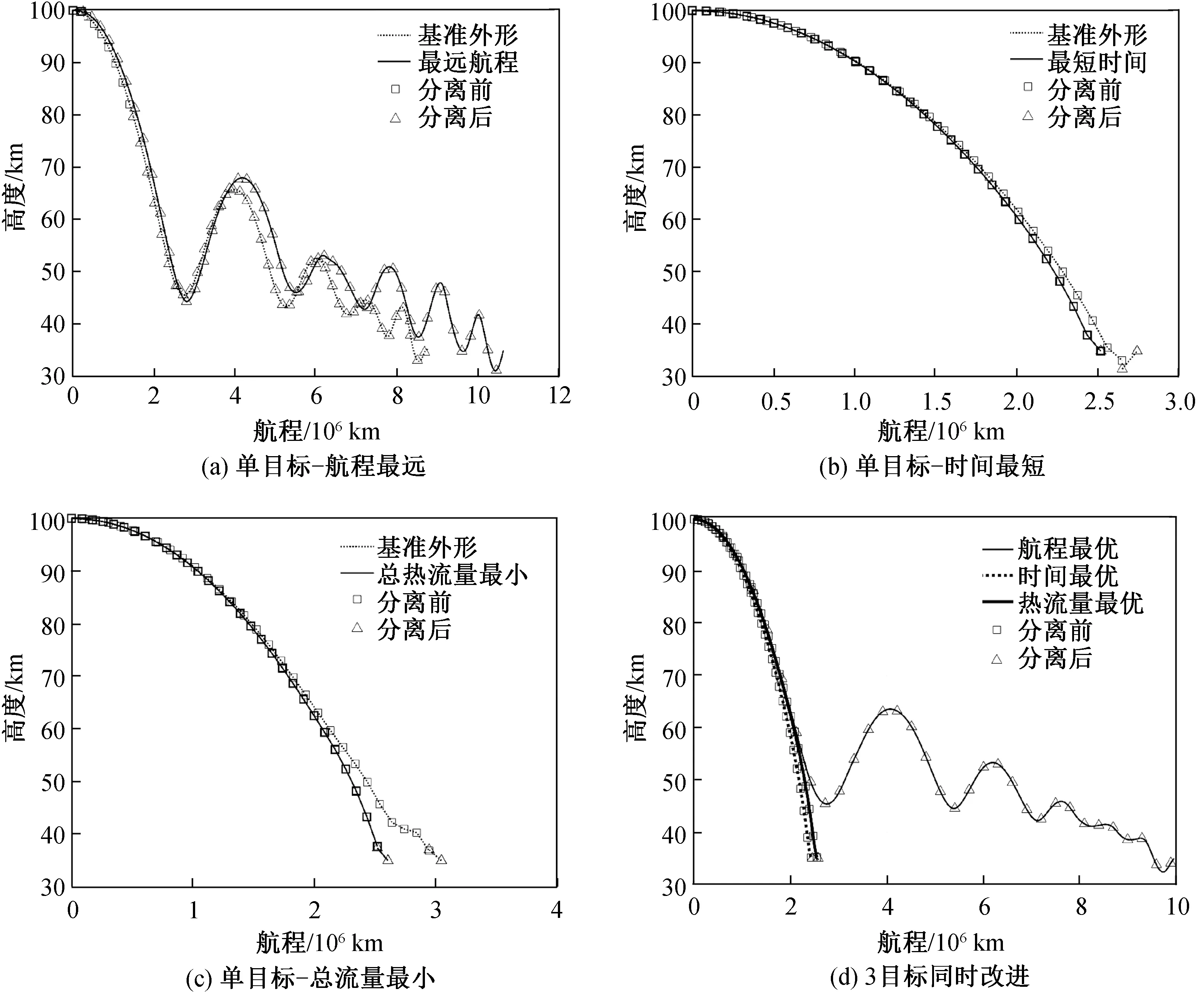
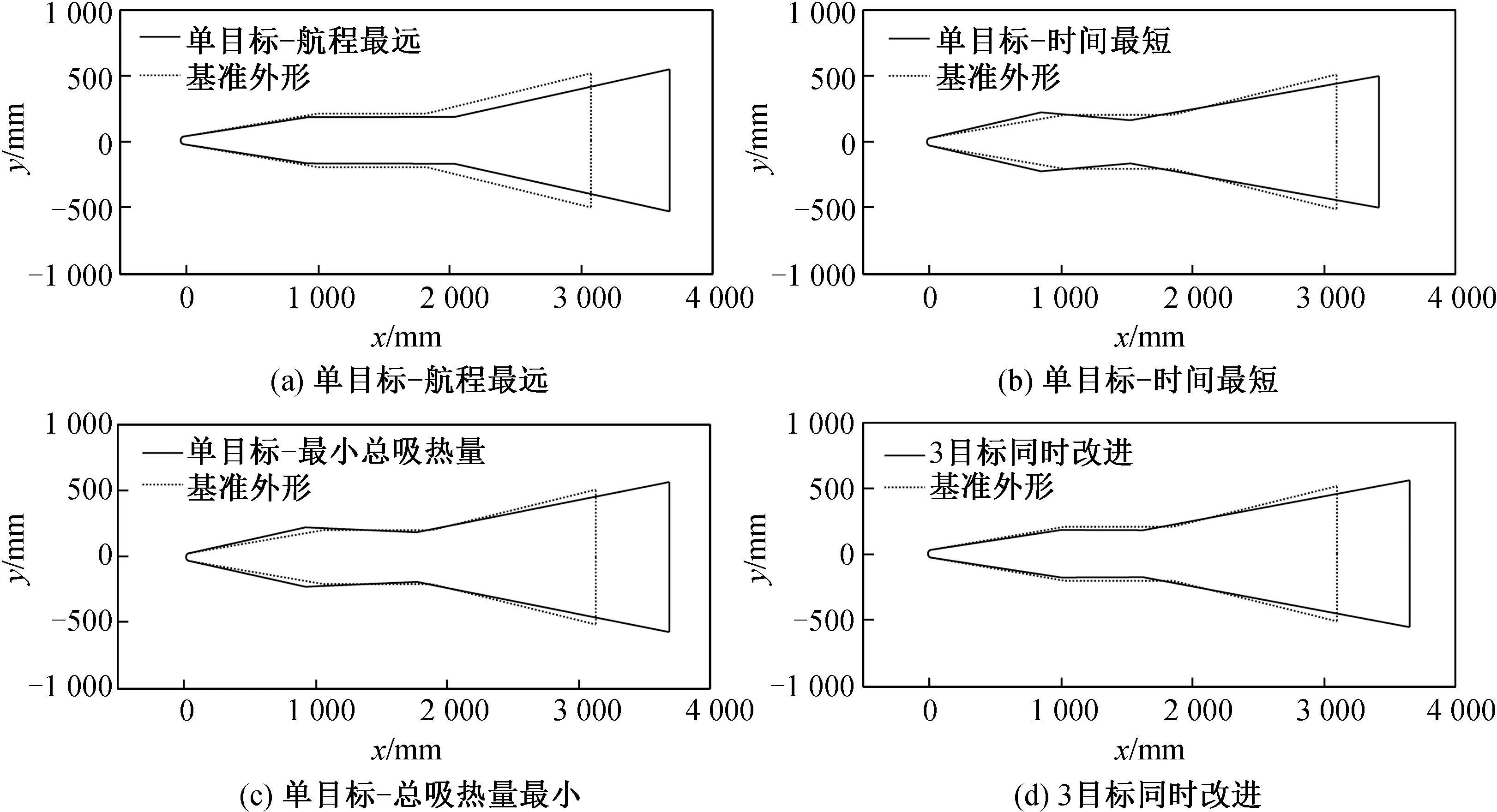
5 结束语
