佩戴部位对加速度计能耗监测准确性的影响：算法的调节效应

2019-04-03陈庆果

中国体育科技 2019年3期

陈庆果，李翔

《“健康中国2030”规划纲要》的实施和全民健身上升为国家战略把科学健身提到了新的高度，随着“互联网+”和大数据热潮的到来，运动类可穿戴设备呈井喷式的出现，各种品牌、各种型号的运动手环、运动手表和运动能耗监测仪层出不穷。但从体力活动测量的原理上看，这些仪器大部分都属于加速度计范畴，均是利用加速度传感器捕捉的客观原始加速度数据来监测运动状况。

在学界，加速度计能耗监测的研究由来已久，早在20世纪80年代初，Montoye等（1983）和Wong等（1981）就进行了一系列开创性的研究，把原始数据合成count值，再将其代入回归方程建立计算模型，成为能耗预测领域的经典算法。后来不断有学者通过丰富建模数据特征、完善count指标体系和利用硬件提升效益等手段不断优化回归模型。近年来，随着机器学习算法的兴起，为了充分挖掘原始数据蕴含的丰富信息提高预测的准确性，不断有学者将不同的机器学习算法引入到能耗预测中，Staudenmayer等（2009，2015）先后将神经网络模型应用到髋部加速度计和腕部加速度计中，研究结果均表明，机器学习算法在非周期性活动的准确性上明显优于传统的以count值为基础的线性模型，Rothney等（2007）和Trost等（2012）针对髋部加速度计的研究也得出相似的结论。但在此领域的研究中，鲜见对不同部位之间两类算法差异的系统比较，缺少对算法效应的整体考量。

针对不同佩戴部位的现有研究也存在同样的不足，例如，在线性回归预测能耗的相关研究中，髋部因其靠近身体的质心而被视为理想的佩戴位置，部分研究结果显示，相比大腿和腕部，髋部线性模型的预测精度显著提高（Preece et al.，2016），但仍然没法准确的预测非周期性活动的能耗（Hendelman et al.，2000）。Swarts等（2000）采用腕部－髋部的混合模型提高非周期性活动的预测准确性，Crouter等（2015）应用分段回归模型的研究却表明，腕部也能准确地预测运动能耗。目前对机器学习算法的探究结果则相对较少，Ellis等（2014）引入随机森林模型，髋部和腕部模型的RMSE分别为1.09 METs和1.00 METs，算法的部位特征不显著，对神经网络模型的研究也显示相似的结果（Montoye et al.，2015，2016），目前来看，还需更多的实证依据以形成概化性的结论。

综上所述，当前的研究主要是探讨单一算法不同部位间预测准确性的差异，或是单一部位间不同算法的差异，鲜见系统探讨佩戴部位和算法之间可能存在的交互效应，算法能否降低佩戴部位对预测准确性的影响也不得而知。本研究旨在通过对部位效应、算法效应及其之间的交互效应进行系统探究，明晰佩戴部位对能耗监测的影响效力，探究算法的应用价值。

1 研究对象与方法

1.1 研究对象

在告知测试内容和健康问询后，经受试者同意确定42人的测试名单（表1）。所有受试者无运动禁忌症，测试前24 h无大强度体力活动，测试均在餐后1 h进行，测试前签署知情同意书。

表1 佩戴部位对加速度计能耗监测准确性测试受试者基本信息Table 1 TheAnthropometryCharacteristicsofParticipant

1.2 测量仪器

本研究采用3个美国产Actigraph-GT3X+（以下简称GT3X+）收集人体活动中不同部位的加速度信息，GT3X+是目前应用最为广泛的3轴加速度计，重量约为27 g，对加速度原始数据的采样频率可以达到100 Hz，内存容量为250 MB。测试前利用Actilife6.0软件进行校对、信息录入和采样频率设置（30 Hz），然后使用相应长度的弹性绑带固定在受试者右侧髋部（右侧髂脊处）、右侧大腿处（大腿前正中线上1/3处）和右侧手腕处（腕横纹处）。每天测试完成后，将数据保存为*.GT3X格式，以便导出加速度原始数据。

能量消耗的标准测量采用意大利产的CosmedK4b2便携式气体代谢分析仪（以下简称K4b2），该仪器采用每口气呼气法进行测量，准确性得到广泛验证，被视为金标准。为保障测量精度，整个测试前更换氧电池，每天测试均对仪器进行预热和定标。测试中，为确保GT3X+和K4b2的数据同步，测试人员在每一分钟第一秒按压仪器主机上的Enter键开始正式记录数据，并使用心率带同步监控受试者心率，以此确定活动之间的间隔时间。每天测试完成后，将数据保存为*.xpo格式，后期再转制为周期为30 s的数据库。

采用恒康佳业HK-6000身高体重仪测量受试者身高和体重，使用韩国VIVENTE-GOLD体成分仪测量体脂率。

1.3 测量方案

活动方案由4类20项体力活动构成（表2），分别为5项静息类活动、6项走跑活动、5项生活方式活动和4项体育活动，每项活动的时间为5 min（跳绳除外），活动之间的时间间隔视心率的恢复状况而定，一般为1～5 min。实验方案基本囊括日常体力活动的主要类型和项目，兼顾项目的周期特征、肢体特征和强度特征。

表2 佩戴部位对加速度计能耗监测准确性测试项目Table 2 List of Physical Activies

整个测试分两个阶段进行，第1阶段进行形态学指标测量、静息类项目和走跑类运动的测试；第2阶段包括5项生活方式活动和4项体育活动测试。

静息活动和生活方式活动在实验室模拟的生活情景中进行，要求受试者按照日常状态完成活动。走跑活动（除自由走跑）在德国h/p/cosmos公司生产的Pular跑台上进行。体育活动中乒乓球和羽毛球采用多球练习的方式，受试者不捡球；跳绳和篮球运动均要求受试者按自己节奏进行。

所有测试共需120～140 min，温度控制在18℃～25℃，相对湿度在50%～60%。

1.4 原始数据的处理与指标的合成

研究将建立一般线性回归模型和神经网络模型，因模型数据要求不同，将前期导出的*.GT3X文件转换为*.CSV的原始文件后，分别进行不同的数据预处理和特征指标的提取，数据处理的时间周期为30 s，每个项目第一个和最后一个30 s的数据不纳入统计口径。

线性回归模型的输入指标为count值，虽然GT3X+的配套软件actlife6.11可直接导出，但因数据处理的过程是其商业机密，未见相关文献报告。为提高数据处理结果的普适性，本研究未直接使用软件导出的count值，而是参考相关研究成果自行合成，数据处理分为3个阶段：1）滤波：滤除噪声频段和干扰及特定波段频率，参考孙泊等（2013）的研究，采用二阶巴特沃兹0.2～10 HZ带通滤波器对X、Y、Z三轴的原始加速度数据进行滤波；2）数据的修正：为了去除重力趋势对各轴的作用，同时对3个轴过滤后的加速度数据进行去趋势处理，公式为特征指标的提取：由于原始信号均是双向的，先取绝对值后再计算积分，同时考虑到加速度计佩戴在不同部位，会出现传感器的运动轴与实际运动情况不能有效匹配（Schaefer et al.，2014），故采用三轴的数据合成矢量计数（vector magnitude，VM），公式为来表征count值。

神经网络模型特征指标的提取中，为降低模型的运算负担，同时鉴于Migueles等（2017）的研究显示，频阈指标在提高能耗预测准确性的作用有限，本研究仅选取时域类指标，直接从原始数据中（未滤波）提取每个轴每30 s中的9个指标：M、SD、Min、Max、P10、P25、P50、P75 和P90，3个轴共计27个指标，前4个指标的选取依据Montoye等（2015）的研究成果，后5个指标来自Staudenmayer（2009）的研究。

1.5 数据统计和分析

采用MATLAB7.0对数据进行预处理和指标的合成，形成每30 s的各种特征指标（过程见1.4），然后从K4b2导出*.xpo文件，并转换获取METs/30数据库，与加速度特征指标按照时间点一一对应形成数据库。

使用Matlab7.0软件进行6次留一交叉验证分析，分别建立髋部、手腕和大腿的神经网络模型和线性回归模型（共计6个模型），并输出相应的预测值。留一交叉验证分析以每个受试者为单位，在42名受试者中，每轮留1个个体数据作验证，其他41个个体数据建模，总共轮换进行42轮，得到42个测试结果，用参数的平均值来表征模型。该方法相对于传统的holdout检验（将数据分为两组，一组建模和一组验证），可以从有限的数据中获得尽可能多的有效信息，避免陷入局部的极值（范永东，2013）。

采用均方根误差（root-mean-square error，RMSE）指标来判断模型预测准确性，公式为：

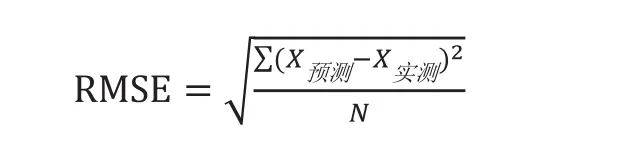
以个体为单位来计算该指标，并作为检验变量，采用SPSS22.0软件运用双因素重复测量方差分析进行佩戴部位和算法交互效应的分析，以及相同模型不同部位之间的比较和相同部位不同模型之间的比较。

使用MiniTAP软件进行等效性检验，以判断各模型预测METs和实测METs测量结果的等效性，标准为：预测均值90%置信区间是否落入实测均值的等效区间（μ±10% μ）（Nolan et al.，2014），如果落入则接受备择假设：下限＜检验值/校标均值＜上限，可认定两种测量方法等效。

统计分析中显著性水平定义为P＜0.05，高度显著性水平定义为P＜0.01。

2 研究结果

2.1 加速度计能耗方程的建构

2.1.1 不同佩戴部位线性回归方程的建构

手腕、髋部和大腿的线性回归模型见表3，R2分别是0.428、0.702和0.659，SEE分别为1.922、1.415和1.472。髋部模型的斜率最大、腕部模型的截距最大。

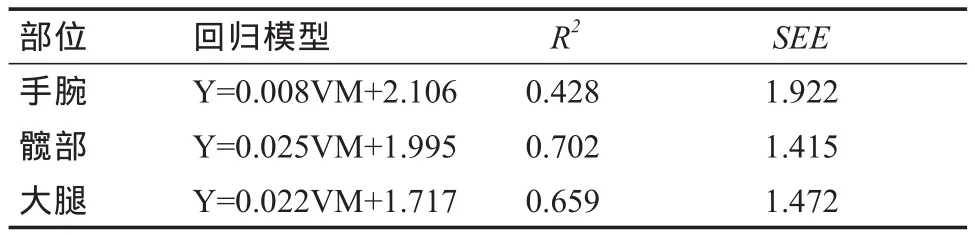
表3 不同部位佩戴加速度计能耗测量的一般线性回归模型Table 3 List of Linear Regression Model of Different Wearing Sites

2.1.2 不同佩戴部位神经网络模型的建构

在对数据采用标准公式Y=（X-Xmin）/（Xmax-Xmin）进行归一化处理后，将输入层和输出层指标数带入吴昌友（2007）介绍的公式（n为输入层指标数、为输出层指标数），确定各个部位神经网络模型的隐层节点数为10个，采用动量-学习率自动调整算法，初始动量取值范围0.2～0.9，学习率范围0.01～0.2，训练网络的最大误差设定0.001。将1 000次作为停止训练的标准。通过对网络结构和参数的多次调整和比较，各模型的平均参数见表4。

2.2 模型在各活动项目上预测准确性的分析

从表5可知，各模型的METs预测值随项目变化的趋势与实测值基本一致，但从同一活动项目预测值的变异上看，不同部位的神经网络模型变异较小，预测的结果较为一致，而线性模型中部位之间的变异较大，尤其是在走的项目和上肢活动为主的项目中。提示，部位对预测准确性的影响可能受到算法的调节，需要进一步使用两因素重复测量的方差分析进行检验。

表4 不同部位佩戴加速度计能耗测量的神经网络模型Table 4 List of Neural Network Model of Different Wearing Sites

表5 不同部位佩戴加速度计的不同能耗预测模型的预测值和实测值Table 5 Predictive Value and Measured Value of Different Models of Energy Expenditure

结合图1可知，相对各部位线性回归模型的散点，神经网络模型各部位的散点均较靠近参考线，通过对平均百分误差（BIAS）的计算，髋部、大腿和手腕3个部位中分别有7个、5个和6个项目的BIAS在±5%以内，在线性回归模型中，这一数值分别为3个、4个和0个。而BIAS在±20%之外的项目数量，线性模型也多于神经网络模型。

2.3 佩戴部位与算法的交互效应分析

本研究中佩戴部位和算法都是类别变量，检验变量为RMSE，按照温忠麒等（2012）的建议，结合数据获取的被试特征，采用双因素重复测量的方差分析进行交互效应的检验。

2.3.1 交互效应检验

表6为球形检验的结果，交互项的Mauchly'sW=0.923，P=0.201＞0.05，检验变量满足球形检验假设，适合进行球形检验，不采用Greenhouse&Geisser方法进行校正。

表6 交互项球型检验Table 6 Sphericity Test of Interaction Items

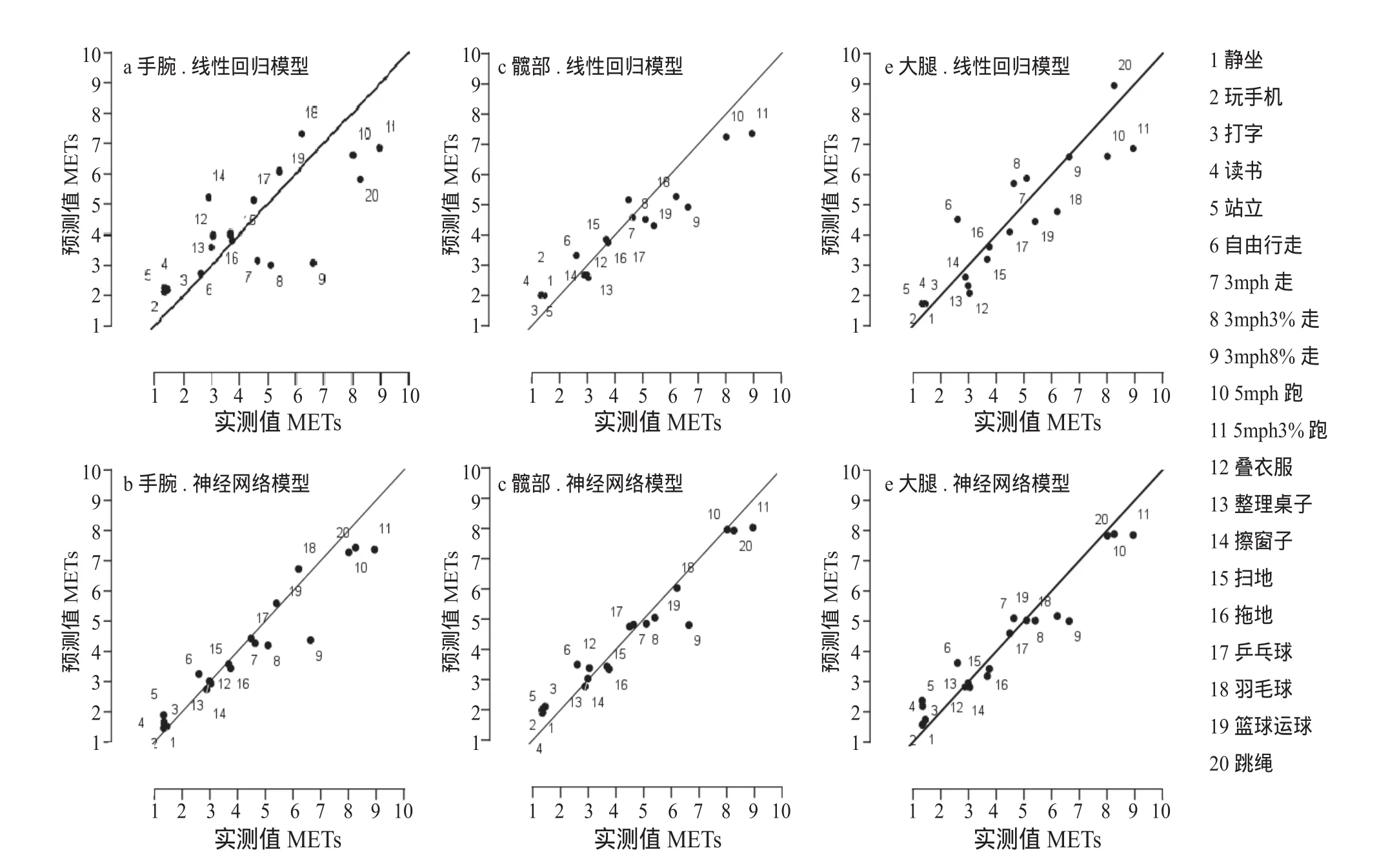
图1 各模型预测值和实测值之间散点图Figure 1. Scatter Plot between Estimated and Measured Values of Each Models

从表7可以看出，算法和部位的交互项存在着统计学意义，F（1、41）=5.376，P=0.006，表明算法与部位存在着交互效应，算法是部位对测量准确性影响的调节变量。

表7 算法*部位交互效应检验Table 7 Interaction Test Table from Algorithms*Sites

2.3.2 不同佩戴部位两种算法测量准确性的多重比较

在交互效应确认的情况下，应进一步明晰各自变量的单独效应，先逐一分析不同部位两种算法的差异。Bonferroni多重比较的结果显示（图2、表8）：在髋部，神经网络模型的RMSE=1.29，线性回归模型为1.31，两者之间平均差值仅为0.018，不存在统计学意义（P=0.293），在大腿和手腕，两种算法的差值增加，分别为0.204和0.279，均存在非常显著性差异（P=0.001和P=0.000）。

表8 不同佩戴位置中两种算法测量准确性的检验Table 8 Test of Accuracy of Two Algorithms in Different Wearing Sites

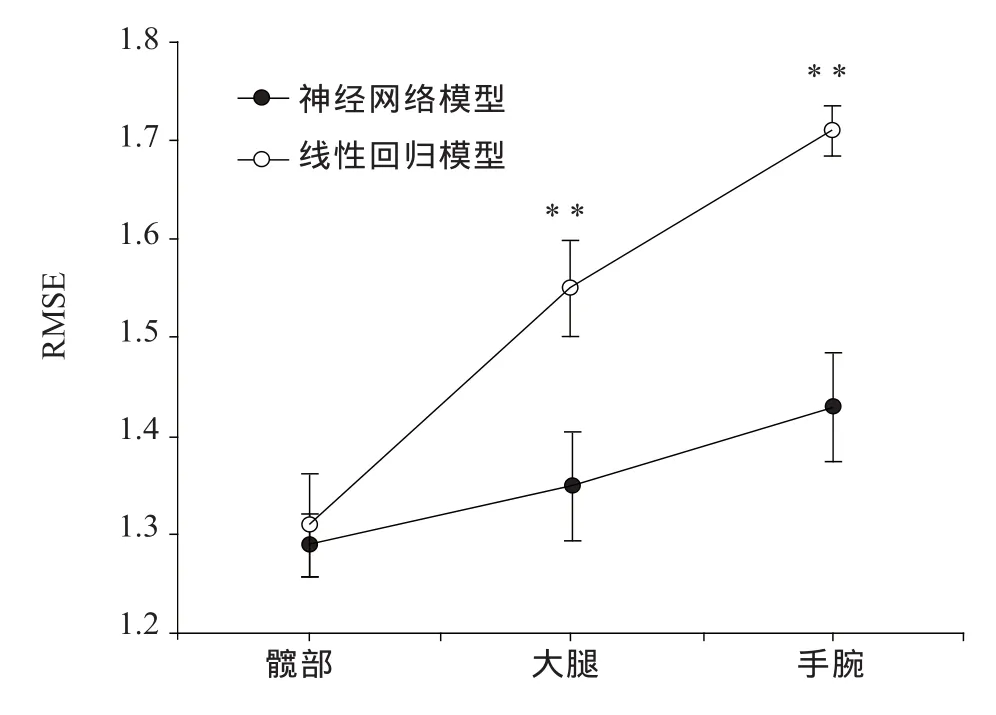
图2 不同佩戴部位中两种算法的测量准确性对比Figure 2. Comparison of Measurement Accuracy of Two Algorithms in Different WearingSites

2.3.3 不同算法中不同佩戴部位测量准确性的多重比较

继续探究佩戴部位的单独效应，分别在两种算法内进行重复测量方差分析。Bonferroni多重比较结果显示（表9）：在线性回归模型中，髋部与大腿、髋部与手腕和大腿与手腕之间预测准确性的差异具有统计学意义，两者之间的差值分别为-0.245、-0.402和-0.152，P值分别为0.000，0.000和0.015；在神经网络模型中，仅有髋部和腕部之间的差异存在统计学意义，而髋部与大腿、手腕与大腿之间的差值均不存在统计学意义（P=0.380和P=0.201），这也进一步表明了神经网络模型可以降低佩戴部位所产生的测量误差。

2.4 各模型的等效性校验

从表10可知，髋部的神经网络模型和线性回归模型以及大腿的神经网络模型预测数值90%置信区间分别为3.81～4.30、3.69～4.27和3.75～4.29，均落在了3.61～4.41的等效区间，可以认定，整体而言上述3个模型预测值与K4b2校标值测量之间具有等效性。

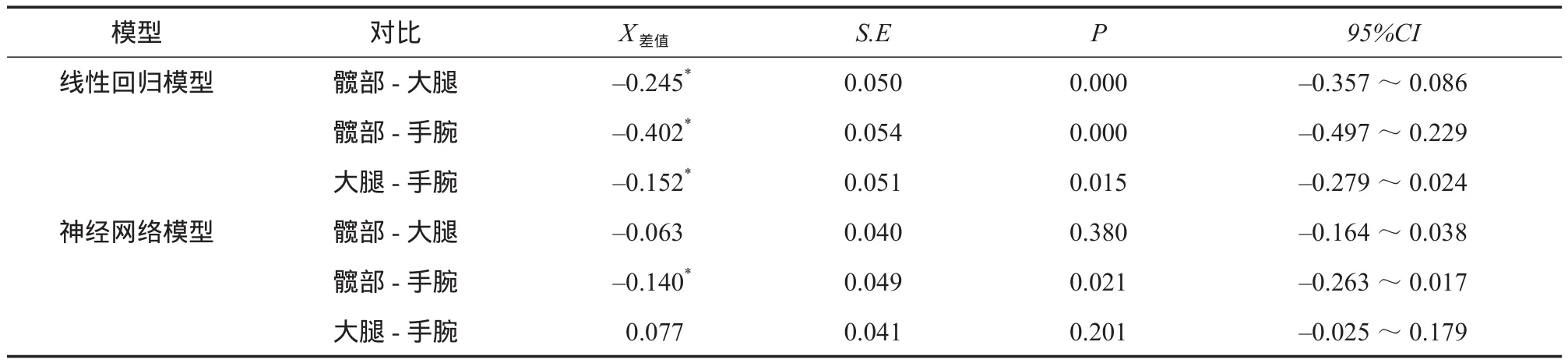
表9 两种算法中不同佩戴部位之间的测量准确性检验Table 9 Accuracy between Different Wearing Sitesin Two Kinds of Algorithms

表10 各模型预测值与校标的等效性检验Table 10 Equivalence Test Table of Model Predictions and Criterion

3 分析与讨论

3.1 实验方案的分析

在日常体力活动能耗测量的研究中，学者们普遍摒弃了早期以Freedson方程为代表的走跑运动实验方案（Hendelman et al.，2000），认为走跑方案难以准确反映日常体力活动的特征，其建构的方程不能准确测量日常生活中的非走跑类活动（Leenders et al.，2006），实验方案的制定必须是走跑方案与非走跑方案的结合（朱琳等，2012）。在此基础上，部分学者在研究中将静息类的体力活动融入到活动方案中，认为静息类的活动虽然梅脱值低，但在日常活动中占据较长时间，不能因其引入方案会影响方程对走跑和非走跑运动的预测准确性而视而不见（Chen et al.，2005）。此外，还有学者认为，在设计活动方案时应该考虑上下肢的运动特征。综上，本研究认为，在进行加速度计预测日常体力活动的能耗研究中，实验方案应是被预测人员日常生活的缩影，在构建时应考虑被试者因素、肢体活动特征因素和活动强度因素，综合搭配，选择适应种类和数量的体力活动，保证方案的代表性。

本研究的实验方案由5种静息类活动、6种走跑类运动，5种生活方式类活动和4种体育活动构成，基本囊括该群体日常体力活动的主要类型和项目，又兼顾了活动的肢体特征和强度特征。坐姿玩手机、坐姿打字和坐姿看书均涉及少量上肢肢体活动，而叠衣服、整理书桌主要是站姿状态下较大幅度的上肢活动，扫地拖地及所有的体育项目均是上、下肢活动兼有的非周期性活动，所有的走跑类活动为上、下肢活动兼有的周期性活动。本方案有6个活动属于小强度的体力活动（＜3 METs），8个活动属于中等强度体力活动（3～5.9 METs），6个活动属于大强度体力活动（≥6 METs），活动方案基本满足强度特征。

虽有研究表明，在走跑运动中，随着坡度的增加，基于回归模型的加速度计能耗预测误差加大，但是鉴于坡道环境下的走跑在日常走跑下占据较大比重，同时考虑到机器学习算法的普适性检验，遂将坡度走跑纳入实验方案中。

3.2 不同算法能耗预测准确性差异的部位效应分析

本研究结果显示，在髋部，神经网络模型和一般线性模型的RMSE分别为1.29 METs和1.31 METs，两者之间的差异无统计学意义，该研究结果得到部分其他研究的支持。Montoye等（2017a）的研究显示，在RMSE指标上髋部神经网络模型仅比线性回归模型高3%，差异不具统计学意义；Freedson等（2011）采用独立样本数据进行评估，结果显示，两种模型的RMSE分别为1.90 MET和2.07 METs，差值也较小。在对能量消耗（energy expenditure，EE）的预测上，研究结果也相似（Rothney et al.，2007）。而Staudenmayer等（2009）用已有模型与神经网络模型进行比较时，结果却显示，神经网络模型的RMSE为1.22 METs，大幅低于Swarts模型（1.77 METs）和Freedson模型（2.09 METs）。在该研究中，对于已有模型，采用的是完全独立的样本数据进行预测，这是导致其预测精度下降的主要原因。总体来看，在同类型数据样本中进行的对比研究，神经网络模型对髋部能耗预测的精度提高的作用有限。Freedsons等（2011）认为，建模数据中包含的活动特征信息有限是造成神经网络模型预测精度难以大幅提高的主要原因。该解释只是部分原因，而在非独立样本数据中出现，相似结果，提示，回归模型输入的特征指标可能在髋部这一佩戴位置已经涵盖绝大部分的运动信息，这也可能是造成两种算法预测精度差异不明显的主要原因。

在腕部能耗预测中，本研究结果显示，神经网络模型与线性回归模型预测准确性存在显著性的差异，Staudenmayer等（2015）使用高频数据得出的结果与本研究相似。目前来看，腕部线性回归算法预测精度低已经形成共识，Montoye等（1983）、Swartz等（2000）和Chen等（2003）的研究显示，其预测值和实测值的相关系数分别为0.36、0.18和0.70。而神经网络模型在腕部加速度计中的预测效力逐渐得到实证支持（Montoye et al.，2015），这主要是因为手腕处的运动信息特征丰富，传统线性回归模型输入指标count数值难以表征，造成信息大量流失，影响预测的精度和准确性。

目前对腿部加速度计预测准确性的研究相对较少，一项研究对比神经网络模型和线性回归模型结果显示，两个模型的RMSE相差高达0.67 METs（Montoye et al.，2017b），大大超过本研究两模型的差距（0.204 METs），究其主要原因，可能与统计分析技术有关，该研究中线性模型使用的是已有模型，这就造成独立样本数据和非独立样本数据的错位比较。

综上所述，似乎存在这样一个现象：越接近身体质心的位置，算法对加速度计预测准确性的影响就越小，或者说，佩戴部位的运动特征越丰富，算法的作用就越大，未来还需大量的实证研究对此形成概化性的结论。

3.3 算法调节佩戴部位对能耗预测准确性影响的效应分析

本研究结果显示，线性模型在髋部、大腿和手腕部位的RMSE分别为1.31 METs、1.56 METs和1.71 METs，且两两之间的差异存在统计学意义。实际上，佩戴部位对线性模型影响的研究由来已久，早在20世纪初Swarts等（2000）就考量了线性回归模型在髋部和手腕测量的准确性，结果显示，两个部位的加速度计预测的决策系数仅为0.317和0.033，虽然两个部位预测差异较大，但整体都低，究其原因，主要是硬件技术限制，使用的单轴加速度计很难捕捉丰富的运动信息。Chen等（2003）的研究采用能量代谢房的测试结果作为效标检验髋部和手腕的回归模型，结果显示，实测值和预测值的相关系数分别为0.9和0.7，因其测试的均是周期性的走跑活动，所以测量的准确性也主要反映的是在走跑活动中的准确性，该研究结果与Hildebrand等（2014）对走跑活动研究的结果相似。此外，Rosenberge等（2013）的研究也表明，两个部位能耗预测准确性存在显著性差异。目前对腿部能耗预测的研究相对较少，Puyau等（2002）采集儿童户外活动的数据进行分析后显示，腿部与髋部都能准确的预测走跑为主的活动能耗，这与本研究的结果有一定的出入，其主要原因还是与活动方案的设计有关，本研究的活动方案运动特征丰富，包含了上肢运动为主的活动，这势必会影响线性模型在腿部应用的准确性。

与线性模型部位之间的预测差异相比，神经网络模型预测的结果截然不同。本研究结果显示，仅髋部和手腕之间的差异存在统计学意义，且RMSE的差值也仅为0.14 METs，而大腿与髋部和手腕之间均不存在显著性差异。Montoye等（2017a）的研究显示，使用神经网络模型预测时大腿和髋部之间无显著性差异，且均显著性低于手腕部，这与本研究结果略有差异，体现在大腿和手腕的差异性上；Strath等（2015）利用时间序列模型预测的结果显示，髋部、踝关节和手腕的RMSE分别为1.05 METs、1.06 METs和1.03 METs，两两之间的差异均无显著性，该研究各个部位的预测误差均低于本研究，尤其是在手腕关节处；Ellis（2014）使用随机森林算法的髋部RMSE为1.18 METs，手腕为1.29 METs，且两者之间的差异也无统计学意义。

整体上看，机器学习算法中影响预测准确性的部位特征没有一般线性模型明显，线性模型不同部位之间预测准确性的差异更大，这也印证了算法能够减少佩戴部位对加速度计测量准确性的影响，与本研究的交互效应检验的结果是一致的。究其原因：1）因为其充分利用原始数据，将其合成为反映原始信息的众多指标，不像传统的线性回归模型，受算法限制只能将原始数据合成单一的count值，不能充分挖掘原始数据中蕴含的丰富信息；2）因为该算法具有“智能”特征，能够自主学习，依据现有数据优化算法，充分利用数据中蕴含的丰富信息。

3.4 计算模型输入指标的探讨

线性回归模型中输入的指标称为counts，通常是用单位时间内的积分值来表征，即加速度值与X轴围成的面积，亦有研究采用SVMBrandes et al.，2012）和SVM的校正指标（Hildebrand et al.，2014），少量研究还尝试使用过MAD指标（Bastian et al.，2015；Vähä-Ypyä et al.，2015）。对髋部加速度计的研究表明，积分值与能耗具有紧密的关联关系。但本研究结果表明，在大腿和手腕位置，积分值并不是合适的输入指标。未来应进一步研究是否有更为匹配相关佩戴部位的单一输入指标，探究是否具有低多重共线性的多元回归指标体系。

机器学习算法的输入指标体中一类是时域指标，一类是频域指标。时域指标因其提取简单、含义清晰而受青睐，并且有研究认为，频域指标适合应用于活动分类上，而在能量消耗预测上价值有限（Preece et al.，2009）。因此，本研究选择每个轴9个时域指标，共计27个指标作为输入指标，从预测的准确性上看，该指标群是满足应用需要的。目前，对指标的筛选和数量的确认缺乏明确的标准，少数研究采用试凑的方法对此进行研究，Kates等（2016）认为，对于活动类型识别的任务，更多特征指标的输入能够提高机器学习模型的准确性；而对于能耗预测的任务，特征指标的数量对预测准确性的影响具有边际效应，Montoye等（2015）的研究结果支持了这一结论。但上述研究对于不同指标组合的确认具有较大的主观性，如何客观地筛选指标是未来研究应该解决的问题。

3.5 本研究的局限

本研究中的受试者并没有包括超重肥胖群体，年龄段也均为18～29岁年轻人，所建立的模型跨样本的信、效度还有待后续研究；在研究方案上，所有活动均在实验室情境下以清单的形式执行，虽然活动项目众多，基本反映该群体日常体力活动状况，且各强度兼而有之，但还是与日常生活的实际情况有一定出入，未来在条件允许和技术成熟的情况下，应注重在自由生活情景下进行能量准确性的考察，进一步提高方程预测的外部效度。