基于改进SARSA(λ)移动机器人路径规划

宋 宇， 王志明

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

由于具有广泛的应用场景，如机械臂运动规划、机器人运动规划等，近年来，路径规划得到国内外学者的关注，路径规划的相关算法被不断提出。从蚁群算法[1]、A*算法、D*算法、RRT算法、PRM算法、人工势场法[2]、优化算法[3]到模糊逻辑算法、神经网络算法、强化学习算法[4]。其中人工势场法在数学描述上简洁、美观,且规划出的路径较安全、平滑，但存在目标点不可达、障碍物附近抖动的问题。针对人工势场法的不足,国内外许多学者提出了改进方法,如文献[5]提出了扇区划分后增加虚拟障碍物的方法,文献[6]提出了预规划路径后增加虚拟质点的方法，文献[7]采用高斯组合隶属函数建立引力点函数，消除了极小值问题。近年来，基于强化学习算法[8-9]已经被初步用于路径规划问题中。SARSA(λ)算法是一种基于值函数的强化学习算法,如果直接将 SARSA(λ)应用于路径规划,会使初次探索随机性和撞墙概率较大,学习时间较长。

文中通过人工势场法的合力引导机制减少了路径搜索时间，首次探索时选择势场合力方向最大的概率最大，再次探索时，Q值最大方向所占的比重增大。仿真实验表明，改进算法改善了人工势场法易陷入局部极值的现象。

1 Khatib人工势场法

Khatib人工势场法是通过计算合力机器人在一个虚拟势场环境中受到的合力来决定机器人下一步的方向，目标点在环境中任一点x产生的吸引力势场值为:

(1)

式中：xd----目标点坐标;

kp----引力增益系数。

如电场力等于电势的负梯度一样，引力为吸引力势场的负梯度，方向由机器人指向目标点。吸引力的大小为:

Fatt(x)=-grad[Uxd(x)]=-kp(x-xd)(2)

单个障碍物在环境中任一点x产生的排斥力势场值为:

(3)

式中：xobs----目标点坐标;

ε----斥力增益系数;

ρ(x,xobs)----机器人与障碍物之间的距离。

如电场力等于电势的负梯度一样，斥力为斥力势场的负梯度，方向由障碍物指向机器人。机器人排斥力的大小为:

(4)

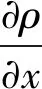
2 SARSA(λ)算法

SARSA(λ)算法是一种基于值函数的强化学习算法，在强化学习中，状态行为值函数的定义为：

(5)

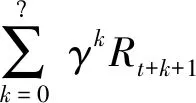
γ----折扣因子。

SARSA(λ)的Q值更新公式可以由式(5)得到，设状态行为对(s,a)的当前Q值估计值为Q(s,a)，机器人在状态s做出动作a后得到奖励r以及到达下一个状态s_，若用r+Q(s_,a_)去估计Q(s,a)，分别给当前估计值Q(s,a)与新的估计值r+Q(s_,a_)一定的概率置信度1-aa和aa，aa为一个0到1的数，则

Q(s,a)=(1-aa)*Q(s,a)+aa*(r+Q(s_,a_))(6)

展开得

Q(s,a)=Q(s,a)+aa*(r+Q(s_,a_)-

γ*Q(s,a))(7)

为了记录获得奖励之前的所有状态动作对，当机器人获得奖励或惩罚时，所有已经记录的机器人经历过的状态动作对都一定程度更新Q值，引入资格迹矩阵E(s,a)，得到SARSA(λ)的Q值更新公式为：

Q(s,a)=Q(s,a)+aa*(r+Q(s_,a_)-γ*Q(s,a))*E(s,a)

E(s,a)=γ*λ*E(s,a)(8)

机器人在一个回合内每走一步，之前步经历的资格迹衰减γ*λ倍。

3 改进算法

若地图大小为n*n，则初始化一个n*n行，8列的值全为k的Q表矩阵，k为一个大于0的正数，机器人可移动方向为上、下、左、右、上左、上右、下左、下右8个方向，此矩阵每一行代表一个栅格的Q值信息。同时初始化一个n*n行，8列的值全为0的资格迹矩阵。

3.1 选择动作

机器人选择下一个动作时，分别计算周围8个邻居格子的a值与q值，式(9)为由合力与Q表共同确定的转移概率。其中的qi值是查询Q表得到的，ai值的确定方法见4.2。机器人最终转移概率由式(10)确定，即50%的概率转移到由式(9)得到的P最大的栅格处，40%的概率转移到q值最大的动作所对应的栅格处，10%的概率向周围8个栅格方向随机移动一步。

(9)

3.2a值

计算当前点(即当前位置)受到的合力大小与方向，将此合力在上、下、左、右、上左、上右、下左、下右8个方向上投影，得到8个分力，将这8个分力的大小(可正可负)从小到大排序，ai为一个大小为1～8序号值，ai值越大，表示此方向合力越大，即机器人向此方向移动的概率越大。

3.3 奖励函数

机器人第一次到达目标点时奖励为R，记录此次机器人经过的总路径长度mindistance，以后每轮比较路径长度与此路径长度，若出现更小的路径长度，则更新最优路径长度mindistance。从第2轮开始的奖励规则由式(11)确定，其中的distance为本次从起点到终点的路径长度，其中的正负号由判断语句决定，若distance小于mindistance取正号，若distance大于mindistance取负号。dis为执行a动作前机器人到目标点的距离，dis_为执行a动作后机器人到目标点的距离。

(11)

3.4 Q值更新公式

如前所述，传统SARSA(λ)的Q(s,a)值是由当前的Q(s,a)值与r+Q(s_,a_)的加权平均得到的，其中Q(s_,a_)是由机器人做出动作a后到达位置s_，再次根据ε-greedy策略选择动作a_，查询Q表得到的。为了充分利用之前探索过的信息，此处将Q(s_,a_)改为

(12)

式中：Q(s_,i)----机器人在位置s_，选择动作i(i为1个1～8的整数，代表上、下、左、右、上左、上右、下左、下右)查询Q表得到的值。

即将式(8)改为:

(13)

式中：n----格子序号。

分别计算s_周围8个格子到目标点的距离加机器人从s_到8个格子的移动距离的和，将8个格子的对应距离值从大到小排序，n为格子的距离值的序号，即距离越小，n值越大，n为1～8的整数。

4 仿 真

文中在PyCharm2017.1.2环境下进行了仿真实验，学习率aa为0.01，折扣因子γ为0.9，资格迹衰减因子λ为0.9，其余参数的设置见表1。

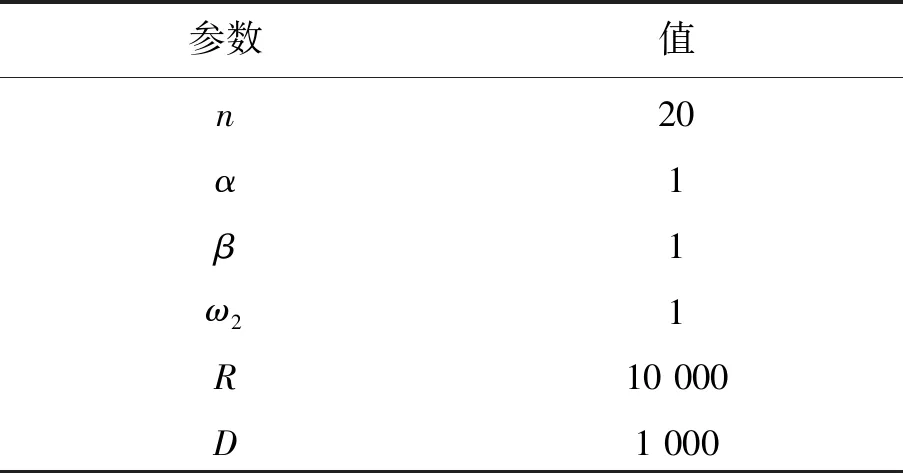
表1 参数设置

4.1 人工势场法目标点不可达地图环境

在合力为0的栅格附近人工势场法出现了在障碍物附近抖动的情形，如图1所示。

SARSA(λ)算法路径规划结果和改进算法路径规划结果分别如图2和图3所示。

图1 人工势场法路径 图2 SARSA(λ)路径 图3 改进算法路径

栅格地图大小为20×20，起点为左下角方块，终点为上方圆形，障碍物为黑色方块。图3中五角星为改进算法100次迭代输出的最优路径。传统SARSA(λ)容易撞墙而无法在100回合内找到目标点(见图2)，五角星为传统SARSA(λ)算法100次迭代中机器人所经过的所有路径点。

4.2 人工势场法目标点可达地图环境

在人工势场法与改进算法都能找到目标点的情况下，这里比较了直接应用SARSA(λ)算法与改进算法的从起点首次到达目标点用时，100次迭代内，成功到达目标点的路径的平均路径长度，100次迭代内，成功到达目标点的路径最短路径长度与从起点到达目标点的平均用时，相关指标对比见表2。

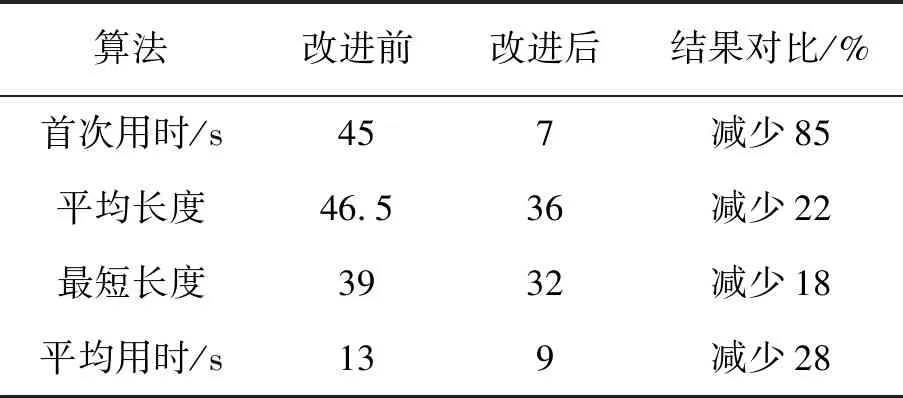
表2 算法结果对比

SARSA(λ)算法100次迭代输出最优路径如图4所示。

改进算法100次迭代输出最优路径如图5所示。

图4 SARSA(λ)算法路径图

图5 改进算法路径图

5 结 语

由于SARSA(λ)具有随机性与记忆性，寻路过程中随机挣脱极小值点的概率被增大。仿真实验表明，相比直接应用SARSA(λ)于路径规划，势场力的引入大幅减少了路径规划所用的时间，由于SARSA(λ)具有随机性与记忆性，一方面克服了传统人工势场法的目标点不可达的缺陷,另一方面增加了寻找到更优路径的概率。