基于决策者偏好的乡村旅游扶贫效率研究※——以秦巴山区陇南市为例

尚清芳

（陇南师范高等专科学校，甘肃 成县 742500）

乡村旅游扶贫作为一项重要的产业扶贫工程，对其效果需要客观的评价，对其的投入产出效率应有科学的测算。当前，乡村旅游扶贫备受关注，已成为学术研究热点之一[1-7]。这些研究主要集中在乡村旅游扶贫的精准识别、扶贫效应、路径选择等方面，而乡村旅游扶贫效率研究较少。乡村旅游扶贫效率是指特定时间内，以旅游扶贫既有的技术、资金、人力、资源投入所能实现的最大旅游产出，即乡村旅游扶贫的配置效率，这是当前乡村旅游扶贫研究的重点之一。国内许多学者对乡村旅游扶贫效率的研究主要集中在2015年以后[8-15]。在研究内容上，大多基于研究区域年度数据，对某一区域旅游扶贫效率进行评价，如高雪莲、丁文广根据2010-2014年陇东南地区旅游扶贫投入产出指标原始数据，计算出该区域5年的旅游扶贫总效率；耿长伟等以六盘山地区57个贫困县为例，根据2015年该区域旅游扶贫相关数据，测算出该区域旅游扶贫效率。在研究方法上，定量研究成为主流，主要借助数学统计模型为研究工具，如曹妍雪、马蓝首次运用三阶段数据包络分析方法对民族地区旅游扶贫效率进行评价；王凯等综合运用多种数学分析手段，建立产出导向SBM模型，对大别山旅游扶贫试验区扶贫效率的时空演化进行研究。在现有文献资料还可看到，当前国内学者乡村旅游扶贫效率大多以国家、大区域、省域为研究对象，小区域扶贫效率研究虽不多，但由于对小区块旅游扶贫效率分析更具现实意义，因而应予以关注。本文在借鉴国内外旅游扶贫效率相关研究基础上，运用数据包络分析方法，建立评价指标体系，对投入、产出指标权重受决策者偏好或指标重要程度影响的乡村旅游扶贫效率进行研究，根据陇南市2018年乡村旅游扶贫资料和数据，进行计算和分析，并对陇南市各区县乡村旅游扶贫效率进行了排序。

一、研究区域概况与研究设计

（一）研究区域概况[7][9]

秦巴山区陇南市地处陕、甘、川三省交界地带，下辖1区8县，有深度贫困县5个，总人口万人，总人口287.42万人。秦巴山区是国家集中连片特困地区，陇南市当前贫困人口31.69万人，贫困发生率13.4%。2018年，该市建成升级美丽乡村示范村81个，75个村被列为全国“乡村旅游扶贫重点村”，农家客栈734家，床位6550张，农家乐1270户，旅游专业合作社42家，旅游商品生产加工专业户450户；陇南市旅游接待1412万人次，旅游综合收入70.8亿元，其中乡村旅游接待688万人次，乡村旅游收入13.4亿元，乡村旅游直接从业人数2万余人，带动间接从业人数5万人。

（二）研究设计

1.评价指标体系的建立[12][14][16-18]和数据来源[19-21]

为对某一区域旅游扶贫进行DEA超效率评价，先需要构建符合当地旅游扶贫实际的评价指标体系，合理选择投入指标和产出指标。对国内近年旅游扶贫效率评价研究的投入和产出指标归纳整理。

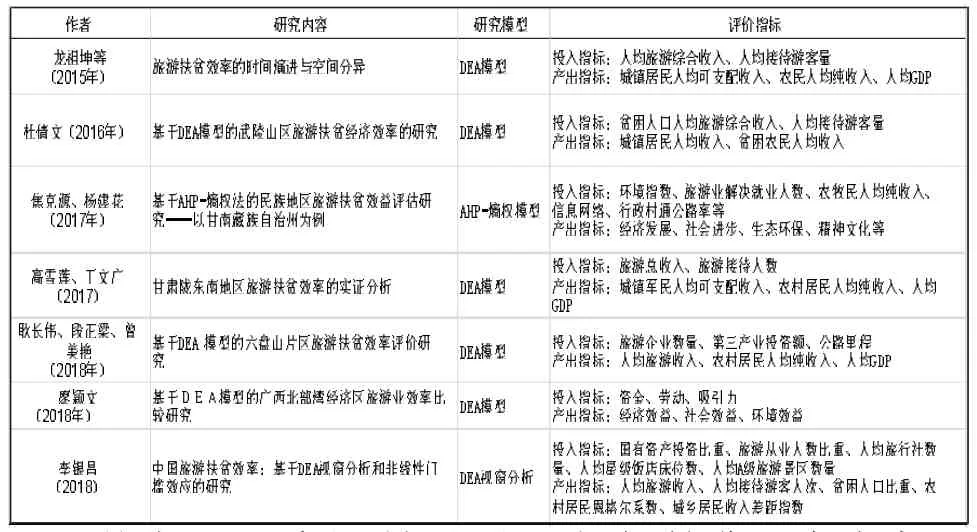
表1 旅游扶贫效率评价指标构建参考表

从表1可看出，针对不同地域、扶贫研究内容以及不同研究模型下，选取的旅游扶贫投入和产出指标有明显差异。但大多数的旅游扶贫效率研究都将资金、游客接待量等作为投入指标，产出指标中选取人均旅游收入等。本文结合秦巴山区陇南市旅游扶贫的实际，选取对乡村旅游扶贫效率影响较大的资源环境、资金、人力（2018年数据）作为乡村旅游扶贫效率评价投入指标，选取经济、社会、生态效益为产出指标，并以上述6个投入-产出指标构成乡村旅游扶贫效率评价指标体系（见表2）。

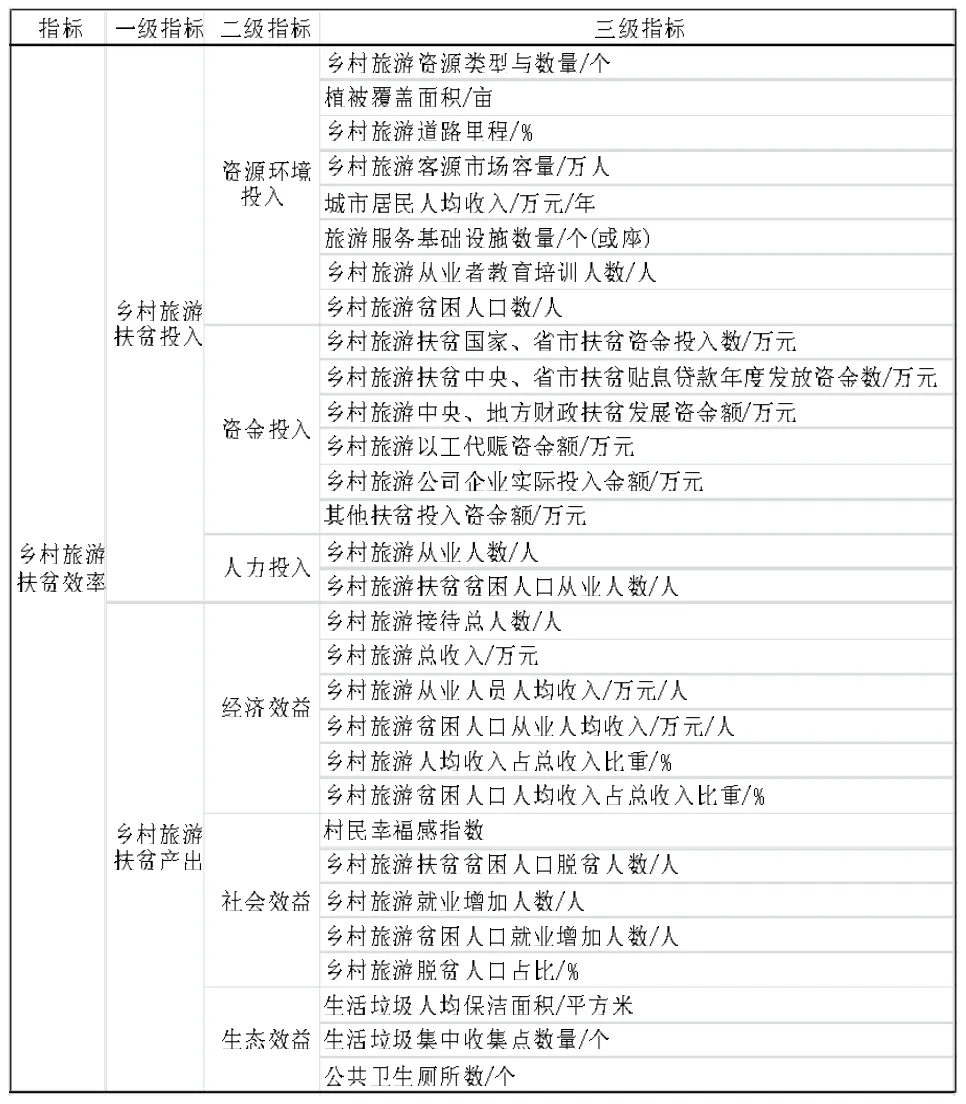
表2 乡村旅游扶贫效率评价指标体系

本文数据来自《甘肃发展年鉴2018》、《2018年甘肃省国民经济和社会发展统计公报》、《2018年陇南市国民经济和社会发展统计公报》陇南市统计局统计分析资料、陇南市扶贫办年度工作报告，以及部分区县旅游和扶贫统计资料。

2.研究方法

旅游扶贫是多投入、多产出的动态过程，扶贫效。，、产出函数关系，也无须对投入、产出指标值做无量纲化处理，同时还无须对指标做权重假设，排除了主观因素的影响，从而使评价结果更具客观性。但是，在乡村旅游扶贫中，不同地域和时间的旅游扶贫政策、资源禀赋、资金投入对扶贫效果的影响程度，即评价指标的重要程度或决策者偏好是不一样的，这是需要优先考虑的问题。本文参考文献[11][22-25]提到的超效率DEA方法，构建含有最优前沿面和最劣前沿面的基于决策者偏好的二阶段超效率DEA模型，对乡村旅游决策单元DMU（陇南市各区县）整体有效性排序。

相对于传统的DEA模型如C2R 模型和BC2 模型，这一方法的优点在于：1、以往的DEA模型通过测算各决策单元与最优前沿面的距离来确定决策单元的相对有效性，但当相对效率值均为1 时，决策单元之间难以相互比较排序。本文提出的超效率DEA模型，是同时基于最优前沿面和最劣前沿面的，能对集中在最优前沿面或最劣前沿面的决策单元进行效率评价，解决了决策单元在最优或最劣前沿面时，决策单元效率值为1 时相互无法比较的问题。2、一般认为，DEA模型用于处理多投入多产出的多目标决策问题时，其最大的优势是由于其不需做出权重假设，从而排除主观因素的影响而具有较强客观性。然而，事实上DEA模型的决策单元DMU中的个别指标由于权重的缺失，又难以体现其重要程度。例如政府通过乡村旅游扶贫项目的实施，期望增加贫困人口的旅游收入实现乡村旅游扶贫的目标，在政策上的重视以及资金投入的加大往往对乡村旅游扶贫效率有极大影响，即在乡村旅游扶贫中，投入、产出指标的重要程度是各不相同的，因此，对评价单元DMU各指标权重的忽视有时会得到背离现实意义的效率评价结果。这体现在：一方面，某一指标权重系数过大，易导致个别DMU虽有效但C2R模型评价该DMU只是相对有效；另一方面，传统的DEA模型得到的结果是难以体现决策者对个别指标的重视或偏好程度的。因此，本文中基于决策者偏好的二阶段超效率DEA排序方法，第一阶段运用最优效率和最劣效率对基于偏好的决策单元合理排序，第二阶段结合第一阶段的测算数据，对各决策单元整体进行排序，能较好的满足现阶段乡村旅游扶贫中提高贫困农民收入等目标的现实的效率评价需求。

第一阶段：体现决策者偏好或指标重要程度的超效率DEA模型

假设有n个决策单元DMUi（i=1,2,…，n）评价指标构成相同，每个决策单元包含k个独立子系统。设DMU的第 h（h=1,2,…，k）个子系统的输入、输出变量为：

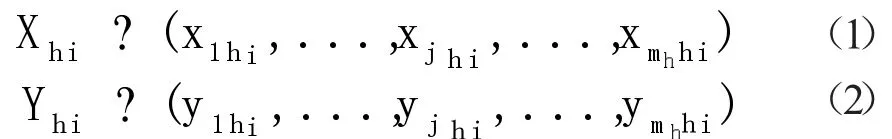
这里，Xhi，Yhi＞0，mh,sh分别表示 DMUi的第 h 个子系统的输入、输出维度。

假设决策单元DMUi0的第h个子系统超效率为φh0，U1r、U2r分 别 为 模 型（4）、（5）的 系 数 ，λ（0≤λ≤1）为决策者偏好或指标权重。建立基于决策者偏好参数的超效率DEA模型[11][22-29]：

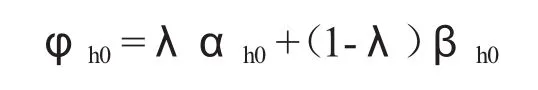
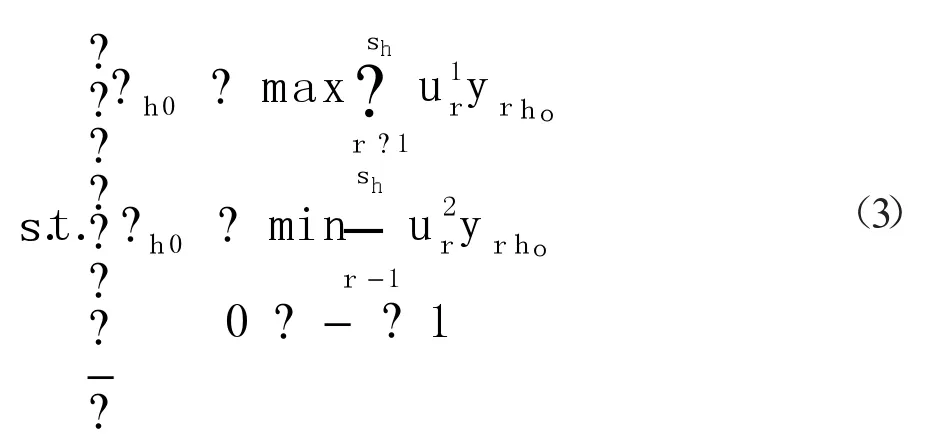
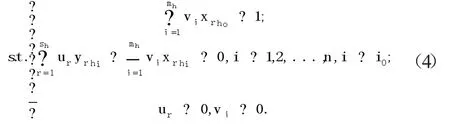
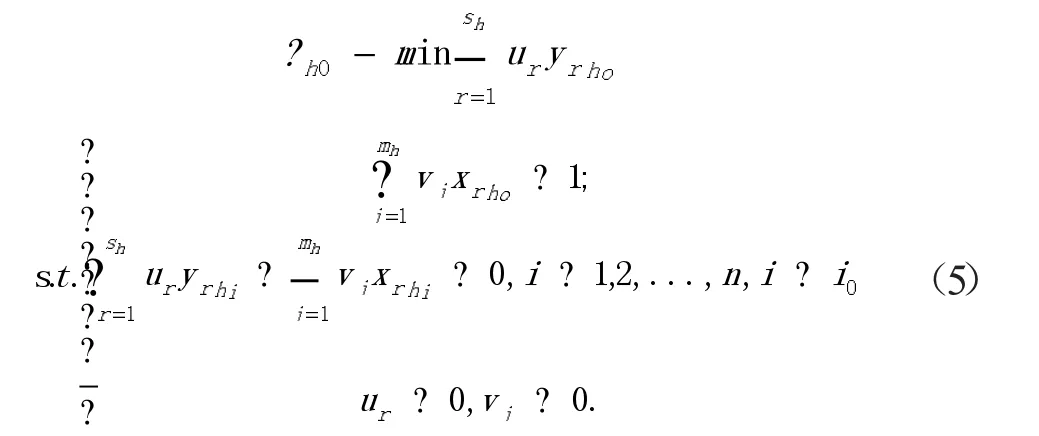
这里，αh0为最劣前沿面的超效率、βh0最优前沿面的超效率。αh0值越大该决策单元距离最优前沿面越近，决策单元越优，若αh0≥1，则该决策单元在最优前沿面上，是有效决策单元。βh0值越大，该决策单元距离最劣前沿面越远，决策单元越优，若βh0≤1，则该决策单元在最劣前沿面上，是无效决策单元。

结合模型（3），利用Lingo软件计算出决策单元DMUi的超效率向量：

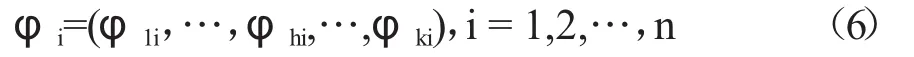
第二阶段：决策单元整体有效性排序模型。

为准确分析各决策单元DMUi的相对有效（纯技术有效），避免非最大生产规模决策单元相对有效评价出现失误，参考Charnes等（1984年）提出的C2GS2模型，建立基于第一阶段输出的非径向DEA（C2GS2）模型：

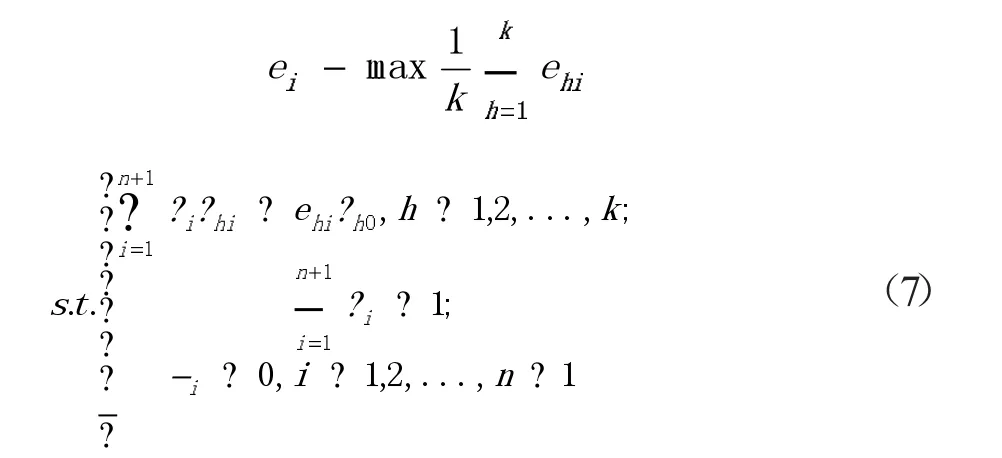
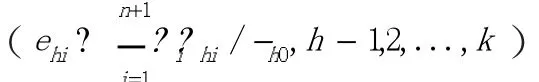
二、结果与分析

基于表1的乡村旅游扶贫效率评价指标体系和统计数据，按照基于决策者偏好的二阶段超效率DEA排序方法，分别运用模型（3）和模型（7），确定mh≤8，sh≤6，k=6，可计算出各决策单元DMUi（i=1,2,…，9）的最优超效率值αhi和最劣超效率值βhi。

表3中数据的说明：α11＞1,β11＞1，表明该决策单元DMU1,11，即第1个决策单元武都区的第1个子系统位于最优前沿面上，距离最劣前沿面较远；α62＜1,β62＜1，表明第2个决策单元文县的第1个子系统在最劣前沿面上；α68＞1,β68＞1，表示第 8个决策单元徽县的第4个子系统在最优前沿面和最劣前沿面交界上；上述情形之外的决策单元（αhi＜1,βhi＞1，）在最优前沿面和最劣前沿面之间。

假定决策者偏重最优效率，令λ=0.8，得出9个决策单元6个子系统的最优效率偏好度为0.8的超效率值（见表4）。

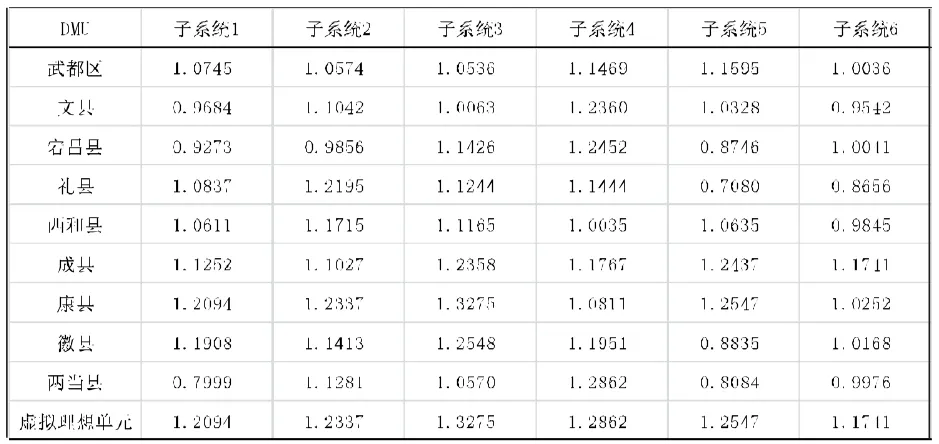
表4 陇南市2017年各区县(DMU)乡村旅游扶贫超效率值

根据表4，利用模型（7）分别计算每个区县的最优目标函数值，并对结果排序，见表5。

表5 陇南市2017年各区县(DMU)乡村旅游扶贫超效率整体排序表

综合表5的整体排序结果和表3子系统计算结果，可看出该排序方法能较好体现决策者偏好。表3中，康县、成县除子系统 6（αhi＞0，βhi＜0，在最优前沿面和最劣前沿面交界上）外，其他所有子系统的决策单元都在最优前沿面上（αhi＞0，βhi＜0），可看出决策单元康县和成县有效性明显强于其他区县，而且β66＞β67，因此在表5中看到的二县排序都靠前，并且康县排名在成县之前。决策单元武都区和西和比较，武都区和西和分别有4个和2个子系统在最优前沿面上，并且分别有2个和4个子系统在最优和最劣前沿面交界上，决策单元武都区有效性强于西和县，因此根据模型（7）计算后的排序结果表5显示的西和县排名在武都区之后是符合情理的。两当县虽然有3个子系统在最优前沿面上，1个子系统在最劣前沿面上，但是其基于决策者偏好的整体超效率值与虚拟理想决策单元的超效率值差距较大，整体有效性较差，因而根据模型（7）计算的结果显示两当县排名靠后。决策单元宕昌县有3个子系统在最劣前沿面，只有1个子系统在最优前沿面，但是其引用模型（7）计算出的整体超效率值更接近理想决策单元效率值，因而有效性较好，因此排序在礼县、两当之前。

三、结语

乡村旅游扶贫，应坚持因地制宜、因势利导的原则开展，那么，不同地域和时间的旅游扶贫政策、资源禀赋、资金投入对扶贫效果的影响程度，即评价指标的重要程度或决策者偏好各不相同。以往的在运用传统DEA超效率进行乡村旅游扶贫效率评价时，不仅因忽视指标重要程度或决策者偏好导致评价结果缺乏现实合理性，而且存在最优前沿面的有效决策单元难以排序问题。本文提出的基于决策者偏好的二阶段DEA模型，较好的解决了以往乡村旅游扶贫效率评价的排序难题，实证分析验证了该方法的合理性和可行性。