水毁作用下管道有限元模拟及计算分析

张 翼

中石油贵州天然气管网有限公司 贵州 贵阳 550023

1 引言

管道水毁灾害是长输管线中发生次数最多且分布地区最普遍的地质灾害。埋地管道产生悬空的主要原因是由于土体中水的作用或表面径流的冲击，从而导致表面覆土流失，而穿越河流的管道，则可能由于河流流速或方向的改变，导致其覆土缺失，产生悬空管道。由于水毁导致的管道悬空具有可预测、可加固以及可保护的特点，故研究水毁导致的管道悬空对管道维护工作具有指导作用且具有代表性。

2 管道有限元模拟分析

本文使用ANSYS对管道进行有限元分析。建模采用SOLID185单元模拟土体，土体本构模型采用Drucker-Prager(D-P)模型，土体参数为弹性模量3.2 5*107Pa，泊松比0.4 ，内聚力50000Pa，密度密度2000kg/m3，摩擦角20°。

采用SHELL181单元模拟管道，采用非线性面-面接触模型模拟管-土相互作用，其中目标面单元采用TARGE170单元，接触面单元采用CONTA174单元。管材物理力学性质为管材型号为X80，密度7850 kg/m3，弹性模量207GPa，泊松比0.3 ，σ1为544MPa，E2为6210MPa，屈服强度555-675MPa。

天然气管道外径1016mm，壁厚15.3 mm，按设计压力10MPa输气，输气时气的质量按计算得来的等效密度考虑到管道上，天然气密度取85kg/m3。

灾害体主要沿垂直于管轴方向发展，在地质灾害发生后形成。横向悬管管道水平，两端有土体，中部悬空，土体长度取为悬空管道长度一半。考虑到对称性，只建立一半模型。土体上表面和悬空自由面不约束，底面全约束，其他面除竖向位移外均约束。管道悬空中部对称约束，另一端只约束轴向。

2.1 完全悬空

弹性极限悬空长度下的计算结果：悬空长度280m，最大von Mises应力535MPa，最大应变0.0 02667，最大竖向位移8.2 231m。

2.2 承受均布荷载

取覆土厚度2.5 m、2m、1.5 m、1m和0.5 m，达到弹性极限悬空长度时的计算结果如下。

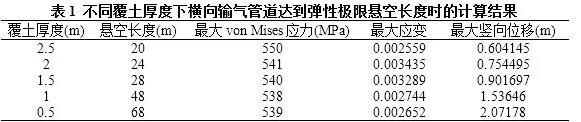
在悬空长度较短时，相比于悬空，覆土均布压力是影响管道受力和变形的主要因素，此时管道的最大von Mises应力和最大应变均位于悬空段中部上表面。而随着悬空长度的增长，悬空则慢慢起到主导作用，最大位移则始终位于管道悬空段中部，也是竖向位移。

2.3 横向悬管承受水流冲击

管道在悬空且承受不同流速水流冲击下达到弹性极限状态时的计算结果如下。

随着水流流速的增加，管道的最大von Mises应力、最大应变和最大位移均在增加。水流流速较低时（3m/s），该悬空长度下管道的应力水平很低，即低流速水流对悬空管道的冲击影响很小。水流流速15m/s时管道的最大von Mises应力为551MPa，没有超过管材最低屈服强度。随着流速的不断增加，管道所能承受的弹性极限悬空长度越来越小。

3 水毁作用下横向悬管受力及计算分析

3.1 完全悬空

（1）悬空管段受力模型

水毁灾害引起埋地管道的悬空管段可看作悬垂跨越管道，悬空管段两端土壤受一个横向的拉力H，管道内输送介质和自重单位载荷q造成管道下垂，下垂高度为f。

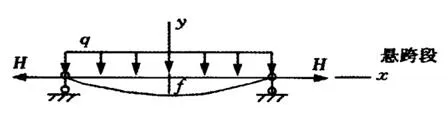
图1 悬空管段受力模型

（2）计算分析

天然气管道的管材型号为X80，弹性模量E为207GPa，屈服强度为555MPa；管道管外径D为1016mm，壁厚t有两种分别为15.3 mm和18.4 mm；管道内天然气的密度约为85kg／m3。因此可以计算出壁厚15.3 mm时管道的重量产生的单位长度上的重力qP为3700.3 N／m，管道输气时的重力qP，0为6241.4 N／m；壁厚18.4 mm时管道的重量产生的单位长度上的重力qP为4436.3 N／m，管道输气时的重力qP，0为6945.5 N／m。

取悬空段长度L为280m，悬空深度为8m。计算输气工况时的受力分析。代入数值后求得壁厚为15.3 mm时，I为0.0 0602kg/m2；壁厚为18.4 mm时，I为0.0 0717kg/m2。

综上，采用反复渐进计算方法计算出壁厚为15.3 mm时，上述悬空管段两端的拉力H为1789.4 kN，则拉应力σ为551.8 MPa；壁厚为18.4 mm时，上述悬空管段两端的拉力H为1943.4 kN，则拉应力σ为599.3 MPa。通过对相同管径，不同壁厚的管道应力进行试算的结果可以看出随着壁厚的增加，悬空管段两端的拉应力也逐渐增加，壁厚为15.3 mm时，拉应力未超过屈服强度，而壁厚为18.4 mm时拉应力为599.3 MPa，已经超过屈服强度，故当悬空段长度为280m时，壁厚为15.3 mm的钢管可以承受其拉应力，而壁厚为18.4 mm的钢管则有较高风险。

3.2 承受均布荷载

可见，随着覆土厚度的增加，管道单位长度载荷不断增加，其所能承受的最大悬空管道长度则逐渐减少。

3.3 横向悬管承受水流冲击

在水流的作用下，水下管道会产生悬空段。受水流冲击时管道最大悬空长度Lcr计算公式如下：

式中：fn为悬空管段自振频率，Hz；K为不同端点约束情况的系数；EI为管跨刚度，m；ms为管跨单位长度的质量，它由管道自身的质量m1、管内介质的质量m2组成。

3.3 .1 壁厚对管道最大允许悬空长度的影响

以管径813mm为例，计算不同壁厚情况下，不同水流速度下管道能够允许的最大悬空长度，计算结果如下。

根据计算可知，管道壁厚相同时，随着流速的增加，管道所能承受的最大悬空长度逐渐减少；水流流速相同时，随着壁厚的增加，管道所能承受的最大悬空长度逐渐增加；当流速、壁厚均相同时，输气工况下管道所能承受的最大悬空长度均小于未输气工况；壁厚对管道最大悬空长度的影响较小。

3.3 .2 管径对管道最大允许悬空长度的影响

以壁厚8mm为例，计算管径不同时，不同水流速度下管道能够允许的最大悬空长度，计算结果如下。

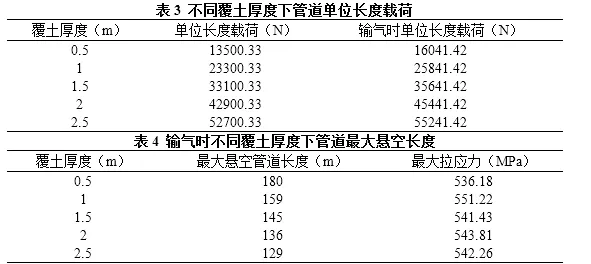
综上可知：管道管径相同时，随着流速的增加，管道所能承受的最大悬空长度逐渐减少；水流流速相同时，随着管径的增加，管道所能承受的最大悬空长度逐渐增加；当流速、管径均相同时，输气工况下管道所能承受的最大悬空长度均小于未输气工况；管径对管道最大悬空长度的影响要大于壁厚对其的影响。

通过对横向悬管的最大悬空长度的理论计算，得出以下主要结论：（1）壁厚对横向悬管最大悬空长度的影响较小，故在实际工程中壁厚的影响可以忽略。（2）管径对横向悬管最大悬空长度的影响较大，随着管径的增加，其能承受的最大悬空长度也逐渐增加，故在有水毁灾害发生的管段，可适当加大管径。（3）随着水流速度的增加，管道能承受的悬空长度逐渐减少，这与有限元建模分析的结果一致，故有限元模拟结果符合理论依据。

由于实际管道所处环境的复杂性，本文仅得出了应力随一些参数的变化趋势，可以在之后的研究中逐步细化；本文对影响因素的分析仅为单因素分析，后续可进行多因素综合分析讨论。