基于RTDS微网的混合储能优化配置研究

张雅雯， 周献远

(1.安徽电气工程职业技术学院， 安徽 合肥 230051； 2.国网安徽省电力有限公司检修分公司， 安徽 合肥 230000)

0 前言

由于能源危机和环境约束，在能源互联网和电改的契机下，各国相继将目光投向新型清洁可再生能源，微网愈发愈吸引了人们的关注。微电网通常是指功率数值在10MW以下，含有不同类型的分布式电源、储能装置、负荷以及控制装置的小型独立系统[1-3]。微网性能的优劣是由分布式电源的性能与其对应的控制策略决定的[4]。

由于光伏发电的不确定性，储能装置的合理配置能有效提高光伏发电系统的可预测性和可调度性。本文使用了大容量、可使用次数相对有限、低功率比的储能装置去补偿小容量、寿命长、高功率比的储能装置，优于单一储能，达到补偿微电网功率波动的效果，提高系统稳定性与经济性。

文献[5]中提出的优化对象为系统的可靠性及运行状态指标，将锂电池和超级电容器的混合储能应用于含独立光伏的发电系统，进行仿真以阐述混合储能的良好性能；文献[6]提出了主储能系统和子储能系统的容量优化配置方法，给定不同工况下系统期望稳定运行的时间指标，通过仿真分析验证方法的有效性和可靠性；文献[7]采用改进的常规细菌觅食算法对已有的模型进行求解，对微网进行实时调度，取得更好经济性；文献[8]着重阐述了传统粒子群优化算法易出现的搜索能力不强早熟收敛、陷入局部最优和早熟收敛等问题。

在基本粒子群算法的基础上，本文采用收敛速度更快、经济性能更优的改进粒子群算法，同时將该算法与RTDS有效相结合，在RTDS平台上搭建含光伏的混合储能模型，将优化前后的数据通过script文件导入RTDS中进行仿真，平抑了光伏发电侧的直流母线电压，同时维持了交流负荷侧电压和功率的稳定，提高了电能质量。

1 混合储能优化配置的算法介绍

1.1 基本粒子群算法

粒子群算法是建立在群体演化的算法基础上的，搜索采用的是位置-速度模型，原理是[9]：种群的规模是N，其中的粒子个体i在飞行过程中主要有在第k次迭代过程中个体寻找到的个体最优值pbest以及整个群体在当前时刻找到的群体中的最优值gbest，由于其简单易实现、可调参数少的优点，应用较为广泛。速度与位置的迭代表达式分别如式(1)、(2)所示：

(1)

(2)

1.2 改进粒子群算法

在搜索后期，种群中粒子的位置缺乏多样性，加之基本粒子群算法存在“局部最优”的缺点，所以要采取措施改进先前的算法，更新自己速度，从而达到避免收敛“早熟”的目的，求得全局最优解。其表达式如式(3)、(4)所示：

(3)

(4)

其中：wmax，wmin是w的最大值与最小值，其数值一般设置为0.9，0.4，stmax，st分别是迭代次数的最大值与当前值。

1.3 目标函数与约束条件

针对光伏系统而言，合理配置混合储能可提高配电侧的供电可靠性和稳定性[10-13]。配置储能装置时要考虑系统的全生命周期费用，包括系统的一次性投资、运行维护费用、折旧费用及装置损坏后的更换费用，将所有的费用折算成总费用。由于系统在运行中存在单体损坏的可能性，设置单体损坏的百分数为2%，目标函数表达式如下：

minC=Ci+Co+Cm+Cd

(5)

Pb≤Phmax,Pc≤Pcmax

(6)

Ebmax≤Eb≤Ebmax

(7)

Ecmax≤Ec≤Ecmax

(8)

(Ebmax-Ebmin)ηbd+(Ecmax-Ecmin)ηcd≥Q

(9)

LPSP(b,c)≤LPSPmax

(10)

式中：Ci，Co，Cm，Cd—依次代表储能系统的购买成本、维护成本、处置成本、运行成本；

Pb，Pbmax，Pc，Pcmax—依次为某瞬间蓄电池的输出功率、最大输出功率值、某瞬间超级电容器的输出功率、最大输出功率值；

Eb，Ebmax，Ebmin，Ec，Ecmax，Ecmin，Q—依次是蓄电池瞬间储存能量的数值、蓄电池储存能量下限、蓄电池储存能量上限、超级电容器某时刻的储存能量、超级电容器储存能量下限、超级电容器储存能量上限、重要负荷不间断供电小时数所需电能；

ηbd，ηcd—蓄电池放电效率、超级电容器放电效率；

LPSP(b,c)，LPSPmax—系统某时刻的负荷缺电率、系统最大负荷缺电率。

2 系统建模

RTDS是基于电磁暂态理论，采取并行运算的多处理器方法，由硬件和软件两部分组成。硬件用于计算和数据输出，软件RSCAD用于搭建电力系统的一次系统及其控制回路，实现对系统的实时仿真、监测和控制。

基于RTDS平台的大、小步长模型搭建含储能装置的光伏并网模型[14-17]，主要包括光伏电板、锂电池、超级电容器、逆变器、架空线、变压器及外接电力系统等，在RTDS上搭建的模型如图1所示：锂电池组和超级电容器分别通过双向换流器与交流母线相连；光伏系统采用增量电导法的最大功率点追踪控制算法最终与正弦三相脉宽调制(SPWM)变换器的交流母线相连。

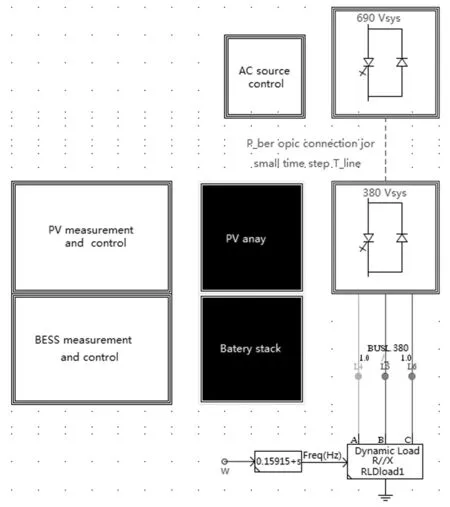
图1 含光伏系统的混合储能一次系统图

2.1 光伏电池阵列建模

2.1.1 光伏电池阵列模型

光照强度和温度的不同影响光伏阵列的输出，根据伏特效应光照射在光伏电池表面可以产生电流和电压。光伏电池等效数学模型如下：

(11)

(12)

(13)

式中：Um，Im，UOC，ISC依次是最大功率点处的电压，最大功率点处的电流，开路电压与短路电流。

2.1.2 最大功率控制模型

为了提高光伏发电的效率，需对其进行最大功率追踪，本文使用电导增量法，将光伏阵列的电压与电流作为输入，把MPPT处的电压参考值与目前算法的状态作为输出端，如图2所示：

图2 MPPT模块

2.2 储能电池建模

2.2.1 锂电池模型

本文采用的锂电池模型，如图3所示，电路中所有非线性元件都是关于SOC的函数，单变量函数用来描述这些元件的特性。

VOC(SOC) =-1.031e-35SOC+3.685+0.2156SOC-0.1178SOC2+0.3201SOC3

(14)

RSeries(SOC)=0.1562×2-24.37SOC+0.07446

(15)

RTransient(SOC)=0.3208×2-29.14SOC+0.04669

(16)

CSeries(SOC)=-752.9e-13.51SOC+703.6

(17)

RTransientL(SOC)=6.603e-155.2SOC+0.04984

(18)

图3 锂电池的等效电路图

2.2.2 超级电容器模型

超级电容器采用经典的RC模型，模型可简化为电容C和电阻R的串联模型，超级电容的电压和电流的表达式如下：

(19)

其中：VO为端电压，VOC为理想电容电压，iC为流经超级电容的电流。

2.2.3 储能电池换流器模型

为了抑制基波电压产生偏差，使电压与电流的相位保持一致，需对锁相环与比例积分进行调节，生成驱动信号的角度由锁相环的输出角度PHI来提供。储能所使用的换流器的控制为双环控制，外环为换流器的外特性，采用比例积分(PI)环节，内环为电流环，经过前馈解耦、比例积分调节器等环节，得到并网电流。与光伏逆变器相比，根据不同场景，储能换流器会自我更新有功控制的目标，最大效能地吸收和发出有功功率。储能换流器模型如图4所示：

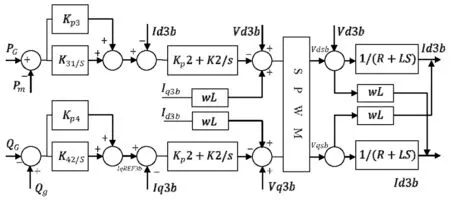
图4 储能换流器模型框图

3 算例分析

根据改进前后的粒子群算法，以某地区2011年的光照，温度及平均日照时数等数据为例，以光伏组成的发电系统为优化对象，容量、功率为约束条件，合理的配置系统的储能容量数量以达到经济投资最优，具体参数如表1。

优化的结果如下，结果的前两个分别为所需的蓄电池和超级电容的个数，最后一个为最终的最优适应度值，即文中的最小费用，变化图形如图5所示。图6所示为变权重系数的优化结果，图7所示为固定权重系数的优化结果。

表1 粒子群具体参数

图5 不同粒子群算法寻优结果比对图

图6 变权重系数优化结果

从最终的结果和曲线图得知：变权重法收敛速度更快，大概80，而固定权重法需要150左右才能稳定。变权重法所需的蓄电池和超级电容的个数小于固定权重法，最优适应度值即经济性变权重法同样优于固定权重法，达到预期效果。

将改进前后的粒子群算法分别与RTDS平台结合进行仿真，其结果如下：

图8为优化前光伏发电系统直流侧电压，由于光伏发电侧的间歇性和随机性，在0～0.4s内电压极其不稳定。

图9为优化后光伏发电系统直流侧电压，合理配置后的混合储能有效平抑了光伏发电侧的直流电压，使其维持在540V左右。

图8 优化前光伏发电侧的直流电压

图10为优化前负荷侧的电压波形图，由于光伏发电的不确定与电网不友好的特征，电压幅值波动较明显。

图11为优化后负荷侧的电压波形图，将改进后的混合储能数据通过脚本文件导入仿真平台中，有效提高了负荷侧的电能质量，平抑了电压波动。

图10 优化前负荷侧三相电压波形图

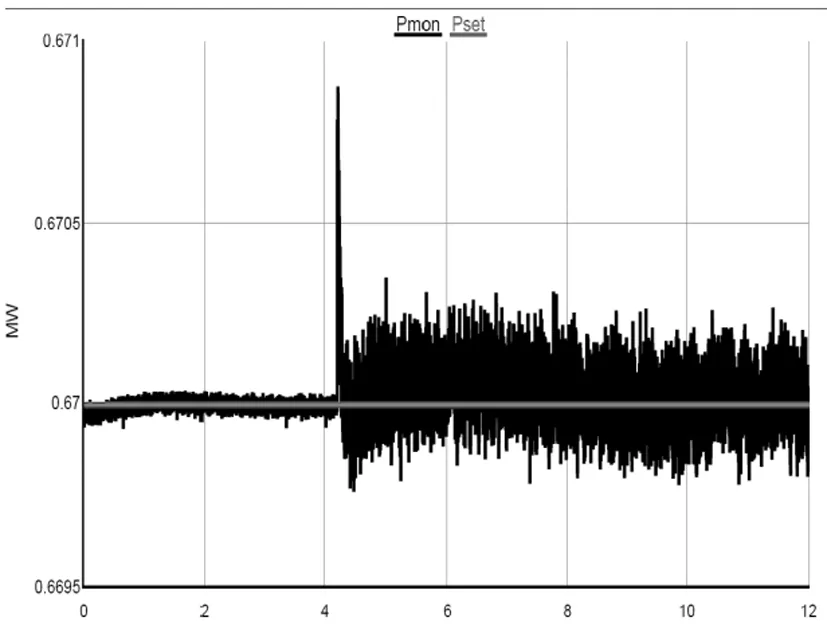
图12 优化前后负荷对比图

图12中Pmon、Pset分别为优化前、优化后负荷侧的有功功率，在合理配置储能容量的前提下，有效调节储能控制器，可以提高负荷侧的电能质量，确保其供电可靠性。

4 结语

本文基于RTDS搭建含光伏的混和储能微网模型，并对模型进行详尽阐述。以某地区2011年的光照、温度及平均日照时数等数据为参考，含独立光伏的发电系统为优化对象，通过对粒子群的研究，以容量、功率为约束条件，系统全生命周期最低为目标，将优化后的结果导入RTDS中进行仿真。结果表明，在收敛速度上，改进后粒子群算法明显优于基本粒子群方法，同时具有较好的经济性，有效平抑了光伏发电系统直流母线电压，保证了系统的供电可靠性，提高了电能质量，对未来新能源技术的发展探索有一定的借鉴意义。