基于TLS-ESPRIT电力信号扰动分析方法的研究
2019-04-01张红飞郭继刚
张红飞, 陈 朔, 郭继刚
(1.国网安徽省电力有限公司培训中心, 安徽 合肥 230022; 2.国网合肥供电公司, 安徽 合肥 230022)
0 引言
电力系统中的正常电压和电流信号应为标准正弦波。但由于各种信号扰动,理想状态的电压、电流信号在供电系统中较难维持,使电网中的电流和电压波形畸变较多[1]。受干扰的电流和电压信号主要包括两部分,基波分量和谐波分量,基波分量是指具有与电力系统提供的电压频率相同的电压频率的正弦信号。谐波分量是指正弦信号,其频率是电源系统提供的电压频率的整数倍。此外,在某些环境中,非整数谐波信号可能出现在电气负载中[2-7]。因此,通过使用新算法,精确谐波和间谐波参数的分析为谐波和间谐波的分析和控制提供了可靠的保证。
本文采用总最小二乘子空间旋转不变性算法求解电压扰动,称为TLS-ESPRIT算法。该算法的特点是结合子空间旋转不变性和总体最小二乘法,通过整体最小二乘法求解特征值和信号频率幅度。实验结果表明,该算法能有效降低噪声子空间的影响,降低计算复杂度,提高估计精度。
1 基于TLS-ESPRIT算法谐波间谐波检测原理
假设信号数学模型为:
x(n)=As(n)+u(n)
(1)
s(n)它是一个初始信号,不会添加任何噪声并包含分谐波信号,含有P次谐波信号。u(n)为高斯白噪声[8],可将s(n)用以下形式表示:
s(n)=akcos(nωk+φ)
式中ωk为角频率,φ为初始相位,ak为幅值。上式改写成复数形式为:
(3)
定义矢量:
X(n)=[x(n),…,x(n+M-1)]T
(4)
U(n)=[u(n),…,u(n+M-1)]
T
(5)
式中M>P,M为时间窗口长度[9]。
X(n)=S(n)+U(n)=ΓΦnA
(6)
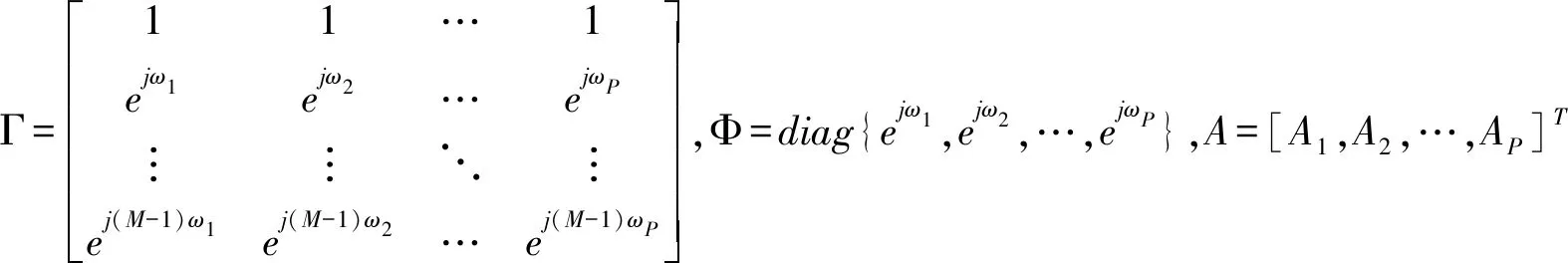
Φ中主要包括谐波信号的频率,在雷达信号空间谱估计算法中被称为旋转因子[10],令:
(7)
可得到S2=S1Φ,求出Φ从而得到P次谐波频率。按以下步骤实现子空间提取与实现:
(1)生成数据矩阵:
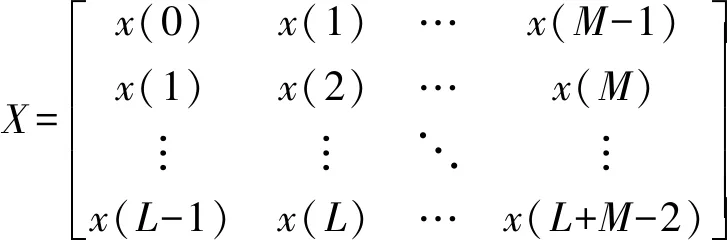
(8)
式中M>P,L>P,L+M为总采样点的数目[11,12]。

(US1+ΔUS1)Ψ=(US2+ΔUS2)
(9)
(10)
所以TLS的解等价于:
(11)
(3)关于上式的解最小范数解的TLS解的方法,通过构造矩阵:
US12=[US1|US2]
(12)
如果能得到一个酉矩阵F,此时使得矩阵F与US12相互正交,则形成的信号子空间与US1、US2列向量相互正交,此矩阵可以由特征分解得出。对式(12)进行奇异值分解以找到正确的奇异矩阵,求出一个2N×2N的右奇异矩阵:
(13)
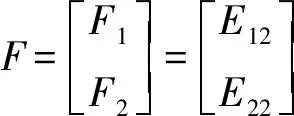
A(f)TT1+A(f)ΦTT2=0
(14)
(4)矩阵Ψ的特征值给出旋转因子Φ,对角线元素是采样频率。φp,fs为抽样频率,谐波频率为:
(15)
2 仿真实验
仿真信号设为:
x(t)=0.08cos(2π×30t)+0.8cos(2π×50t)+0.3cos(2π×170t)+
0.1cos(2π×250t)+0.07cos(2π×350t)+δ(t)
(16)
δ(t)为高斯白噪声,信噪比SNR=30dB,以1 280 Hz的频率采样,其基波幅度为0.8。 谐波频率为250 Hz和350 Hz,相应的幅度分别为0.1和0.07。 有30 Hz和170 Hz间谐波,幅值分别为0.08、0.3。 信号加入高斯白噪声后的波形如图1所示。
在matlab的仿真环境中,总体最小二乘法用于求解信号子空间并检测谐波频率幅度。得到的实验结果如图2所示,具体数值见表1。

图1 仿真谐波信号波形图

表1 TLS-ESPRIT幅值检测结果
3 实际数据分析
利用电能质量分析检测仪从炼钢厂电弧炉提取出电流数据,利用本文所述的TLS-ESPRIT算法对采样数据进行分析。实时信号波形图如图3所示。此时分析仪的采样频率为6 400 Hz,通过本文提出的TLS-ESPRIT算法分析得到的实时信号幅频特性图如图4所示。
通过分析结果可得到该电流信号中含有多次谐波、间谐波信号,通过本文的算法可以将基波和幅值较大的谐波间谐波信号分析提取出来。本组实验表明该算法能处理炼钢厂电弧炉实时数据,具有较好的应用前景。

图3 实时信号波形图
4 结论
本文提出将TLS-ESPRIT算法应用于电力信号干扰检测。仿真结果表明,该算法是一种有效,准确的谐波和间谐波估计算法,可为谐波、间谐波分析提供新的工具。
