柑橘采摘机械臂控制算法研究

郝光鹏，宁志刚

（南华大学 电气工程学院，衡阳 421001）

0 引言

柑橘采摘机械臂运动的控制是采摘机器人研究相关领域中不可或缺的重要部分，它包含了机械臂的运动学建模、动力学建模及运动学逆解算法优化等诸多方面[1-5]。采用仿真方法可以在研究机械臂整体控制系统的基础上，节省大量时间，提前发现问题，大大降低制造过程中的成本。

本文对柑橘采摘机械臂的控制算法进行了研究与优化。调用OpenGL（Open Graphics Library）搭建仿真平台，通过对机械臂进行运动学、动力学方面的建模以及相应算法的实现，完成柑橘采摘机械臂运动控制的仿真[6]。

1 系统流程

首先搭建基于OpenGL的机械臂仿真平台，然后进行运动学方面的建模，并使用MATLAB对逆解结果进行验证，达到预期指标后，进行动力学方面建模与仿真，验证控制算法，以实现对机械臂运动进行准确的控制。具体的流程如图1所示，仿真效果如图2所示。

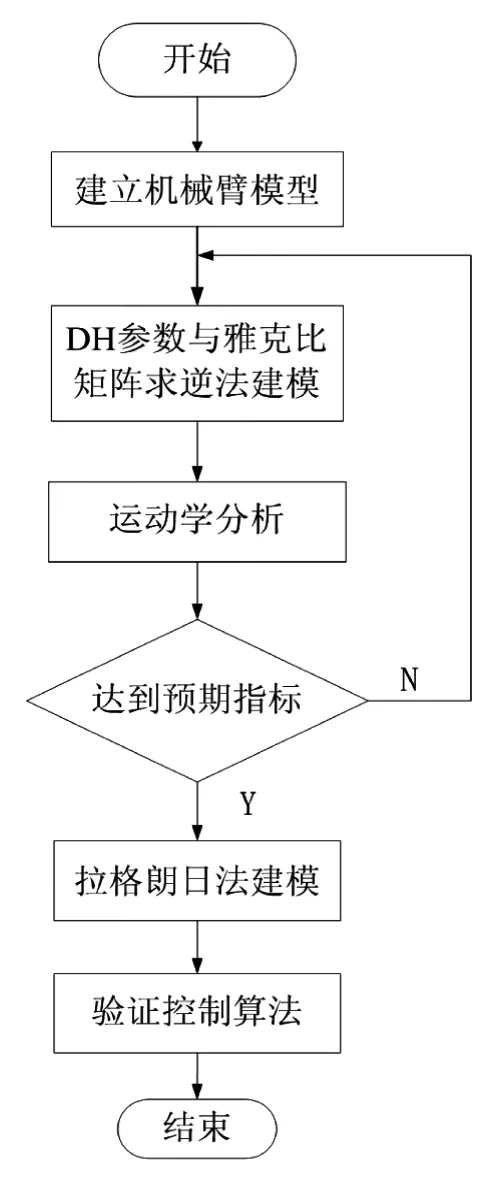
图1 系统流程图Fig.1 System flow diagram

图2 仿真效果图Fig.2 Simulation effect diagram

2 运动学建模

2.1 正运动学

本项目的机械臂由3段连杆与基座组成，全部为旋转关节，共有3个自由度。在考虑基座以及末端执行器的前提下，通过DH参数法，为机械臂各关节赋予相应的坐标系，并列出DH参数表。建立的坐标系如图3所示。其中，O表示所建立坐标系原点，X、Z分别表示所建立坐标系的X轴与Z轴。根据其标号依次为基坐标系1、底座与连杆1之间的坐标系1.5、关节坐标系2、关节坐标系3、机械臂末端执行器坐标系H。

图3 DH坐标系示意图Fig.3 Schematic diagram of DH coordinate system

根据赋予的坐标系得出相应的DH参数，如表1所示。其中，ai表示关节轴之间法线的距离，αi表示关节轴夹角，di表示公共法线在同一轴上的距离，θi表示公共法线在同一轴上的夹角。

表1 DH参数表Table.1 DH parameter table

通过计算得到相邻坐标系坐标变换矩阵T：

矩阵中s和c分别代表sin和cos。根据坐标变换关系可求出从基坐标系到末端执行器坐标系的变换矩阵：

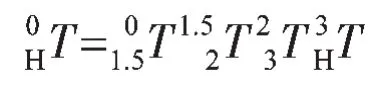
式中 aa表示l2cosθ1+ l3cos (θ1+θ2)，bb表示l2sinθ1+l3sin(θ1+θ2)。

同时，由于柑橘树高度、果实分布等自然特性，在机械臂连杆长度设置时应保证满足柑橘采摘的要求，机械臂的运动空间代表了机械臂的工作范围，使用MATLAB对机械臂运动空间进行模拟。其工作空间如图4—6所示。

图4 工作空间仿真图Fig.4 workspace simulation

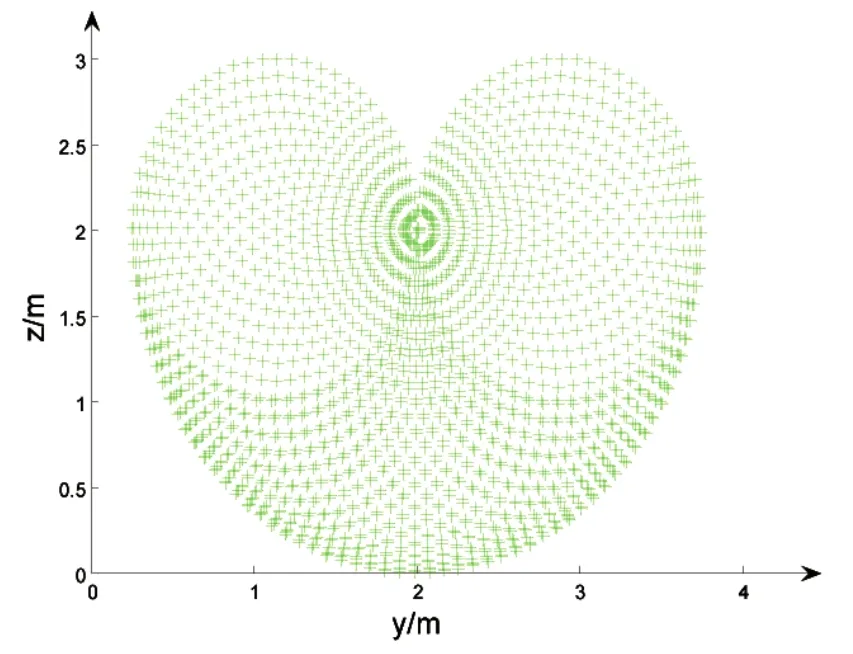
图5 YOZ空间投影图Fig.5 YOZ space projection

图6 XOY空间投影图Fig.6 XOY space projection

由图4可以看出机械臂的工作高度最高可达3 m，水平范围为半径0～2 m的圆。图5为工作空间在YOZ面上的投影，为2个半径为1 m的圆与1个半径为2 m的圆组成的心形图。图6为工作空间在XOY面上的投影，为1个半径为1.5 m的圆，此外，工作空间在XOZ面上的投影与图5相同，由此可得，机械臂运动范围基本覆盖柑橘生长空间，满足柑橘采摘的要求。

2.2 逆运动学

已知机械臂末端位姿求各关节参数的过程称为逆运动学。由于自由度较少，本方案采用雅克比矩阵求逆法进行逆运动学计算。雅克比矩阵作为从关节空间到操作空间的映射，可得如下关系式：

式中 x为操作空间；q为关节空间。

计算流程如图7所示。

图7 逆解框图Fig.7 Block diagram of inverse solution

由图7可得如下表达式：

式中 下标d表示期望值；c表示当前值。

首先，设置末端执行器期望的位置xd，并与当前末端执行器位姿比较，将误差与雅克比矩阵的逆相乘，并将结果送至各关节控制器中，确定各关节位置，然后使用当前关节位置，利用正运动学求出此时末端执行器位姿，与期望位姿进行比较，求得它们之间的差值，然后进行迭代运算，直到dx的值满足要求。

运动学逆解建模完成后，验证OpenGL中的运动学逆解结果。验证效果如图8所示。

图8 MATLAB验证图Fig.8 MATLAB diagram

OpenGL实际末端执行器位姿与MATLAB计算所得的误差约为0.05 m，可以达到柑橘采摘的要求。各关节角度、角速度、角加速度的变化如图9—11所示。

由图9可知，各关节角从（0，0.785 398 2，-0.785 398 2）变化到（0.785 398 2，-0.785 398 2，0.785 398 2），达到了期望的设计目标，由此说明了逆运动学求解的正确性。机械臂在运动过程中，如果速度和加速度突然发生变化，就会导致机械臂抖动。由图10—11可知，角速度和角加速度曲线光滑，在启动与停止时机械臂加速度为0。这表明机械臂运动整体过程中符合连续性要求，运行平稳，达到了期望效果。结果表明，OpenGL使用的运动学逆解可以满足柑橘采摘的要求。

图9 关节角度随时间变化图Fig.9 Change of joint angle with time

图10 关节角速度随时间变化图Fig.10 Change of joint angular velocity with time

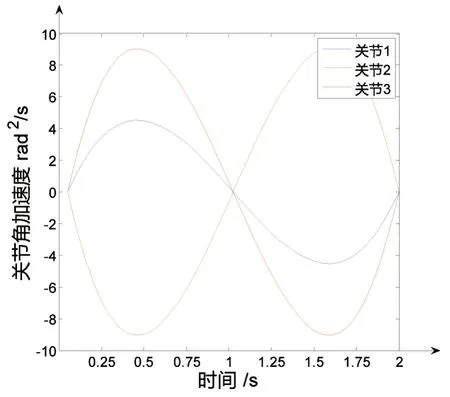
图11 关节角加速度随时间变化图Fig.11 Change of joint angular acceleration with time

3 动力学建模

由拉格朗日法推导得到的机械臂动力学方程为：

式中 M为质量矩阵，由每个关节自身加速需要的扭矩与其他关节加速对该关节的影响叠加而成；v由科里奥利力和离心力组成，表示关节匀速运动对每个关节所需要施加力矩的影响；g由系统势能对关节位置的偏导求得。对于每一行为，每个关节需要克服其之后所有连杆的重力在该关节上的分量；q为机械臂末端执行器位置；τ为力矩。同时在末端执行器受力分析中需要考虑柑橘自身的重量对动力学所建立模型带来的影响，将其转化为关节扭矩，假设柑橘的平均质量为80 g，重力加速度为9.8 m/s2，代入动力学方程左边：

首先，编写程序读取文本文档中已提供的机械臂的长度、质心位置、质量、转动惯量、初始关节角度等参数，以获得质量矩阵。一个n×n的质量矩阵的第i个对角项，表示第i个关节加速运动时需要克服其它所有连杆的质量或惯量。质量矩阵为对称矩阵。一个关节的加速运动同样会造成第二个关节需要施加额外的力矩，以维持其运动状态，这种现象称为动力学耦合。以此可得到如下质量矩阵：

其中 I表示各机械臂转动惯量，θ由DH参数法求得。根据定义代入已给出的机械臂相关参数，得到v及g，从而获得机械臂动力学方程。等式右边的τ是被控量，表示根据建立的动力学模型，让关节按照设定好的轨迹运动时，每个关节驱动器所需要施加的力矩。根据所建立的动力学模型，在MATLAB中使用rne函数可对模型进行验证，其关节力矩与时间、角度、角速度、角加速度关系如图12—15所示。

通过MATLAB对动力学模型的验证，得到图12—15的关节动力学特性曲线。由这些图可知，在机械臂运动的过程中各关节力矩均为线性变化，过渡过程比较平稳，符合OpenGL中机械臂运动状态，表明关节能够按照所期望的速度及加速度运行，同时也进一步表明所规划的轨迹较为合理。

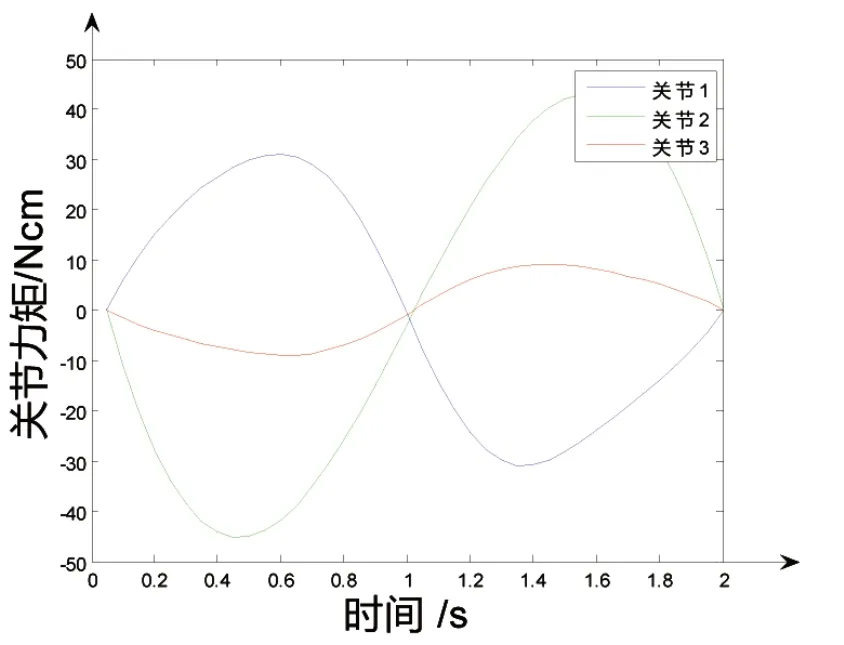
图12 关节力矩随时间度变化图Fig.12 Variation of joint torque with time

图13 关节力矩随角度变化图Fig.13 Change of joint torque with angle

图14 关节力矩随角速度变化图Fig.14 Variation of joint torque with angular velocity

图15 关节力矩随角加速度变化图Fig15.Variation of joint torque with angular acceleration

4 结束语

本文根据柑橘采摘机械臂结构的特点，在OpenGL平台上建立了3D仿真模型，进行运动学以及动力学建模计算，对末端执行器的运动路径进行了规划，并利用MATLAB对仿真结果进行了验证。结果表明，该算法控制效果良好，能满足柑橘采摘机械臂运动控制的要求。