相位差谱法合成人工地震动及其验证

高 陆 军

(中铁五局集团路桥工程有限责任公司，贵州 贵阳 550001)

0 引言

实际地震动是一种强度和频率均具有非平稳特性的随机过程[1,2]。目前常用强度包络函数来刻画强度非平稳，而对于频率非平稳，有学者提出用相位差谱的概念来描述[3,4]。地震动相位差谱与地震动时程强度及频率含量非平稳之间有着重要关系,在地震动空间相关性研究中也有重要应用。

本文考虑地震动空间效应和三维性，基于相位差谱法生成非平稳地震动，并通过频域拟合目标反应谱法对新合成地震动进行幅值精度迭代调整。最后以人工合成的地震动反应谱为目标反应谱，从PEER中选取实际地震动。将该地震动施加到某三跨高墩钢构桥上，对本文提出的人工地震动合成方法进行验证。

1 理论分析

1.1 三角级数法合成地震动

三角级数法是人工合成地震动的常用方法，它具有原理简单、计算速度快编程简单等特点。但该方法得到的地震动反应谱和抗震计算的目标反应谱之间存在较大的误差，精度相对而言不高，不能满足抗震设计要求。

1.2 强度非平稳

为表征地震波强度非平稳，通过三角级数法合成地震波时，用平稳过程与地震动强度包络曲线的乘积来刻画强度非平稳。

三角级数法合成地震动虽然快捷方便，但合成的地震动与实际地震动相比，不具有频率非平稳特性。特别是对于细长型结构如桥梁等，三角级数法不能考虑地震动的行波效应。

2 基于相位差谱的地震动人工合成

2.1 相位差概念

Ohsaki[12]用相位差谱的概念来体现真实地震动相位角之间的相关特性，相位差是指相邻频率对应相位之差，其计算式为：

(1)

其中，k=0.1,…,N/2-1,Δφ(ωk)为相位差；φk和φk+1为相邻两个频率对应的相位角；N为傅里叶变换阶数；相位差的定义域为[0,2π]。

假设频率为0处的相位也为0，则Δφ(0)=0，而其他频率部分的相位角根据相位差定义计算：

φk=Δφ(ωk)+φk-1

(2)

根据式(2)将区段相位差谱合成相位谱，代入公式中，替换随机相位角，即合成基于相位差谱的人工地震动。但此时的人工地震动精度不够，需要进一步迭代修正。

2.2 相位角的统计特性

式(1)为相位差的定义式，不方便用统计的概念来计算相位差概率分布密度函数。根据蒙特卡洛方法，对数正态分布的随机统计参数可以由正态分布的统计参数得到：

(3)

(4)

其中，μ和σ分别为正态分布序列ck的均值和均方差。再通过相位差和正态序列ck的转换关系Δφ(ck)=eck，即可生成具有对数分布的随机相位差谱。

2.3 精度迭代修正

为进一步提高准确率，对合成地震在频域内进行迭代调整，基本步骤如下：

1)根据时频关系，并引入单位脉冲反应函数得到人工地震动的反应谱R(ω,c)：

(5)

其中，Sa(ω,ζ)为人工反应谱;ω和ζ分别为结构圆频率和阻尼比；h(·)为单位脉冲反应函数。

2)将人工合成的各频率分量时程对应的反应谱与目标反应谱之商作为精度控制指标，当该商不在较好精度范围内时，对其幅值修正并再次合成地震动反应谱，再次做商进行精度修正。按照上述方法多次调整幅值，直到控制指标在满意精度范围内为止，即拟合精度迭代计算。

(6)

幅值迭代修正表达式如下：

(7)

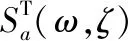
3 准确性验证

3.1 地震波的选取

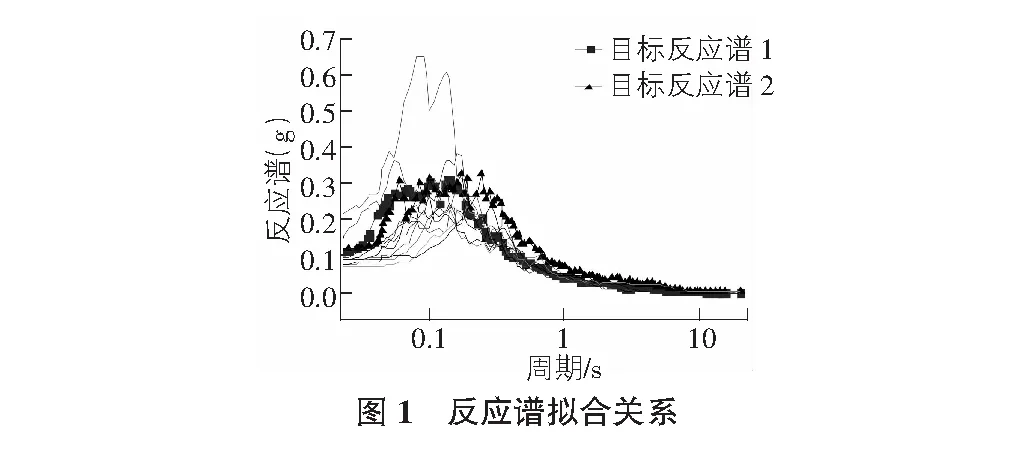
为验证本文合成地震动的准确性，将三角级数法和基于相位差谱法与实际地震动对结构响应进行对比分析。将本文前两者人工合成的地震动转化为反应谱，并以该反应谱为目标反应谱，从PEER中选取十条真实地震动。真实地震动与两条反应谱相互关系见图1。

选取拟合度较好的真实地震动作为分析对象，其加速度时程与反应谱如图2，图3所示。

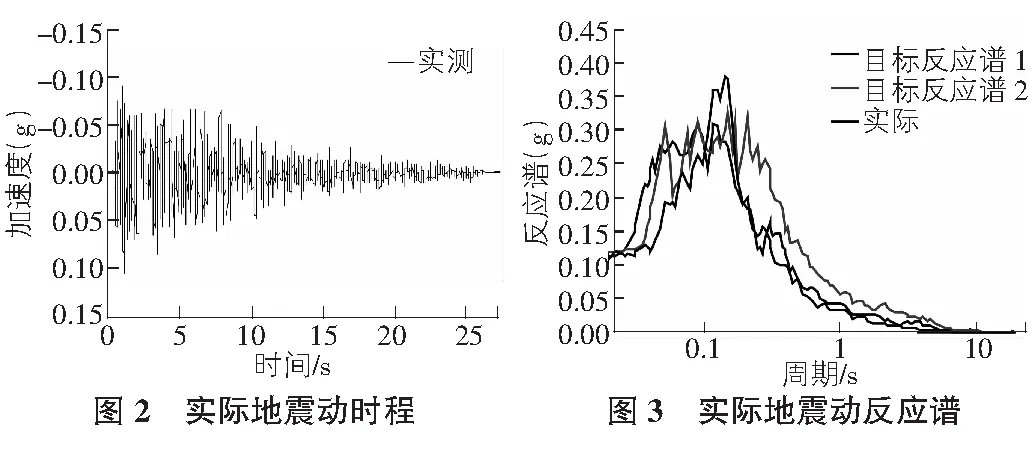
其中，目标反应谱1为相位差谱法合成的地震动反应谱，目标反应谱2是三角级数法合成的地震动反应谱。

3.2 计算模型简介

以某三跨高墩刚构桥为分析载体，其跨径组成为85 m+118 m+85 m，墩高度分别为71 m和63 m。将本文中上述人工合成的两种地震动作为激励输入到全桥中，并与施加的真实地震动进行响应对比。刚构桥梁示意图如图4所示。

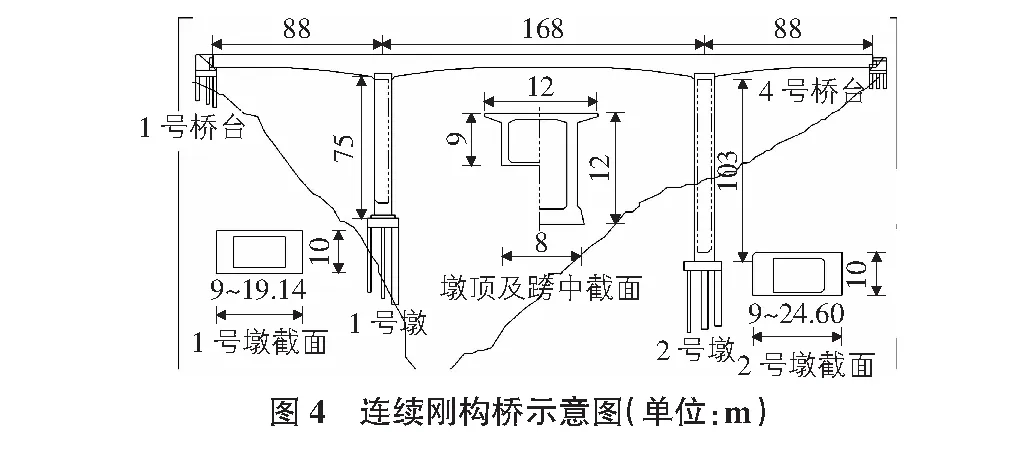
采用一致激励法，分别计算该刚构桥在上述两者人工地震动和真实地震动的结构响应，以此来验证本文方法的准确性。

3.3 响应结果对比验证

借用通用软件ANSYS，建立刚构桥有限元模型，并将合成的地震动和真实地震动作用于该模型中进行动力响应分析。将结构响应峰值作为分析对象，主梁和1号墩的纵向位移如图5，图6所示，桥墩纵向剪力如图7，图8所示，桥墩纵向弯矩如图9，图10所示。

分析对比本文两种人工合成地震动和真实地震动结构动力响应，据图5～图8，可获得如下规律：1)对该桥进行时程分析后，三种地震波产生的纵向位移、墩底剪力和墩底弯矩变化规律基本上一致；2)从图5，图6知，人工合成地震动产生的纵向位移响应略比真实地震动的纵向位移大，但总体规律保持一致；3)三种方法所提供的地震动对结构主梁及墩剪力弯矩响应值基本上保持一致，而墩底处基于三角级数合成的地震动要大一些。

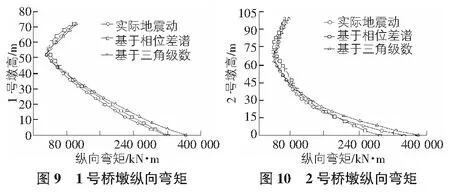
通过时程分析，基于三角级数法、基于相位差谱合成和实测地震动的反应谱大致相似，其纵向的位移、剪力和弯矩分布规律和数值基本一致，故本文合成的地震动具有实际地震动的相应特性，可以用于桥梁结构的地震响应分析。

4 结语

本文基于相位差谱合成人工地震动，得出了以下结论：

1)相位差谱法合成地震动克服了三角级数法缺点，更好地表征地震动强度非平稳和频率非平稳性，更加符合真实地震动，为抗震研究提供了基础；

2)通过蒙特卡洛方法，将具有对数正态分布的相位差谱转化为正态分布的统计参数特性。用目标反应谱对合成的反应谱进行迭代拟合精度修正；

3)基于三角级数法和实测地震波两种方法对基于相位差谱法合成的地震波进行验证，通过刚构桥的动力分析证明其准确性。