2018年全国Ⅰ卷理科解几题研究

江苏省扬州中学 (225009)

戚有建 王 晨

很多高考题看起来很平常，实际上却丰富多彩，都是专家经过精心思考编制出来的，所以有很大的教学价值和研究空间，本文从一道高考解几题出发，首先对问题进行了一般化研究、然后对问题进行类比和逆向研究、最后揭示了问题的深刻背景并进行推广．

一、考题展示

(1)当l与x轴垂直时，求直线AN的方程；

(2)设O为坐标原点，证明：∠ONA=∠ONB.

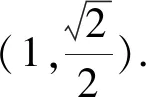
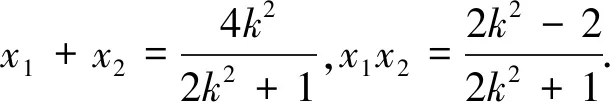
综上得∠ONA=∠ONB.

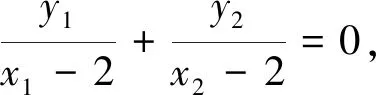
二、一般化研究

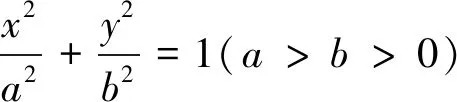
图1

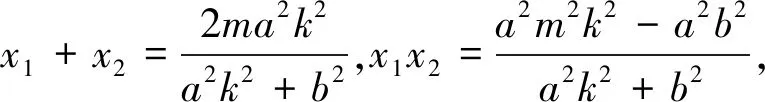
综上得kAN+kBN=0.

图2

说明:(1)命题1中规定了|m|a时(如图2)也成立；

(2)此结论对圆也成立，因为圆可以看作是椭圆的特殊情况.

三、类比研究

既然椭圆有这样的结论，那么双曲线、抛物线也会有类似的结论.

命题3 已知抛物线y2=2px(p>0)及M(m,0),N(-m,0)(其中m≠0)，过点M的直线l交抛物线于A,B两点，设直线AN,BN的斜率分别为kAN,kBN，则kAN+kBN=0.

说明:2015年新课标全国Ⅰ卷理科20题就是由命题3改编而来

四、逆向研究

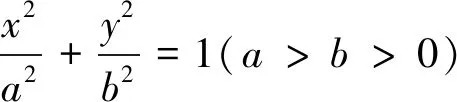
命题6 已知抛物线y2=2px(p>0)及N(m,0)(其中m≠0)，设不垂直于x轴的直线l与抛物线交于不同的两点A,B，若kAN+kBN=0，则直线l过定点M(-m,0).

五、背景研究

在命题1中，有xM·xN=a2，这是偶然还是必然呢？其实是必然，研究后发现本题有丰富的背景，它与极点极线知识有关，实际上，关于极点极线有如下两个常用结论：

(1)如图3，设P为不在圆锥曲线上的点，过点P引两条割线交圆锥曲线于E,F,G,H，设EG,FH交于M，EH,FG交于N，则称MN为点P对应的极线，同理，称PN为点M对应的极线，PM为点N对应的

图3

极线.

图4

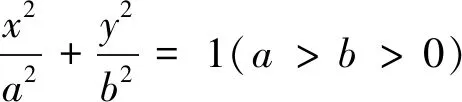
六、推广研究

图5

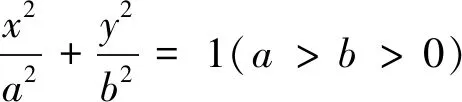
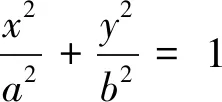
综上得kAN+kBN=2kMN.

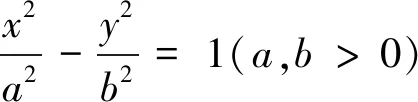
命题9 已知抛物线y2=2px,(p>0)及M(m,0),N(-m,n)(其中m≠0)，过点M的直线l交抛物线于A,B两点，设直线AN,BN,MN的斜率分别为kAN,kBN,kMN，则kAN+kBN=2kMN.