例谈“两组数列项的交或并”
2019-04-01江苏省常州市前黄中学国际分校213161
江苏省常州市前黄中学国际分校 (213161)
陆 德 常 莲
数列是高中数学教学的重点,也是难点,解决数列综合题和探索性问题既考查基础知识、基本技能和基本数学思想方法,更凸显考生综合运用数学思想方法分析问题与解决问题的能力.两组数列中的项合并或取公共项后从小到大依次排列形成的新数列问题一般难度较大,要求较高,需要一定的逻辑推理能力,科学理性的思维方法.
题型一:两组数列项的“并”
例1 (2018年江苏高考数学第14题)已知集合A={x|x=2n-1,n∈N*},B={x|x=2n,n∈N*}.将A∪B的所有元素从小到大依次排列构成一个数列{an}.记Sn为数列{an}的前n项和,则使得Sn>12an+1成立的n的最小值为.
解析:(方法一)此题作为小题来说,最优解法是列举法:
所以n的最小值为27.
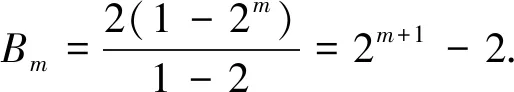
当m=5时,上式为-198>0不成立,此时n=21;当m=6时,上式为226>0成立.此时n=38,此时B5=62,现假设A中共选中t个数,则At=t2,Sn>12an+1,即为62+t2>12[2(t+1)-1],整理得t2-24t+50>0.又t∈N+得t=1(舍)或t=2(舍)或t≥22(t∈N+),所以n=t+5≥27,因此n的最小值为27.
评注:本题考查的是数列综合问题,严格解决比较难下手,但列举法不难得出答案,方法二先指定{an}中的末项2m,通过对m的分析间接得出n的精确值.
甘肃渭河流域地处104°35′~106°44′E、34°05′~35°10′N[1],属河谷温暖半湿润气候区,年均气温10.7 ℃,年降雨量480~610 mm,位置优越,交通便利,是重要的西菜东调基地。韭菜一直是当地农业的支柱性产业,截止2015年,韭菜种植面积0.72万hm2,总产值56 667万元,是全省甚至整个西北地区最大的冬春季节韭菜供应基地。由于独特的气候类型及地理位置,韭菜以其产品鲜嫩、营养丰富、气味芳香等特点,深受全国消费者喜爱,产品远销陕西、青海、宁夏、新疆、广州、武汉、上海等20多个省、市和地区。
例2 已知数列{an}和{bn}的通项公式分别为an=3n+6,bn=2n+7(n∈N*),将集合{x|x=an,n∈N*}∪{x|x=bn,n∈N*}中的元素从小到大依次排列,构成数列c1,c2,c3,…,cn,…
(1)求c1,c2,c3,c4;
(2)求证:在数列{cn}中,但不在数列{bn}中的项恰为a2,a4,…,a2n,…;
(3)求数列{cn}的通项公式.
解析:(1)c1=9,c2=11,c3=12,c4=13.
(2)(ⅰ)设a2n-1=3(2n-1)+6=6n+3=bk=2k+7,n∈N*,则k=3n-2,即a2n-1=b3n-2.所以{an}中的所有奇数项都能在{bn}找到.
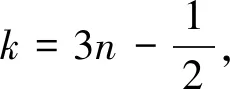
评注:由于{an}和{bn}的公差分别为3和2,故第(3)问中对{an}中的n从被2除的情况分类讨论,对{bn}中的n从被3除的情况分类讨论,判断项的大小,求出数列的通项.本题两组数列均为等差数列.
例3 已知数列{an}的通项公式是an=2n-1,数列{bn}是等差数列,令集合A={a1,a2,…,an,…},B={b1,b2,…,bn,…}n∈N*.将A∪B中的元素按从小到大的顺序排列构成的数列记为{cn}.
(1)若cn=n,n∈N*,求数列{bn}的通项公式;
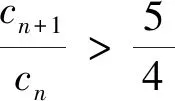
解析:(1)因为A={1,2,…,2n-1,…},A∪B中的元素按从小到大的顺序记为{cn},且cn=n,n∈N*;又因为5,6,7∉A,则5,6,7∈B,所以等差数列{bn}的公差为1,且3是数列{bn}中的项;因此3只可能是数列{bn}中的第1,2,3项.当b1=3时,则bn=n+2;当b2=3时,则bn=n+1;当b3=3时,则bn=n.
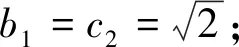
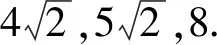
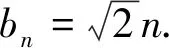
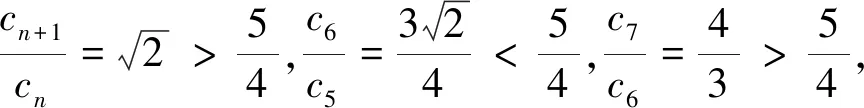
评注:本题考查了等差数列和等比数列的综合运用,对元素2采用分类讨论的方法求得数列{bn}的通项公式,体现分类讨论的思想.
题型二两组数列项的“交”
例4 两个集合A={-3,0,3,6,…,a100}和B={15,19,23,27,…,b100}都各有100个元素,且每个集合中元素从小到大都组成等差数列,则集合A∩B中元素的最大值为.
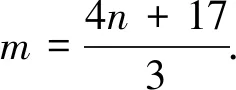
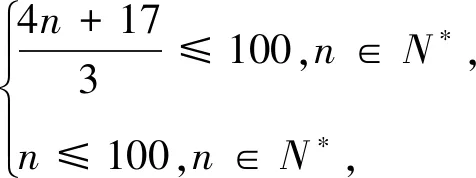
评注:求两数列中的公共项,即寻求两组数列项之间的联系,一般令am=bn转化为关于m,n的不定方程,再根据题设条件结合整数性质求解.
例5 已知数列{an}的通项为an=7n+2,数列{bn}的通项为bn=n2.若将数列{an},{bn}中相同的项按从小到大顺序排列后记作数列{cn},则c9的值是.
解析:(方法一)令am=bn,即7m+2=n2,所以7m-7=n2-9,7(m-1)=(n+3)(n-3),令n+3=7k或n-3=7k,所以n=7k-3(k∈N+)或n=7k+3(k∈N).因此n=4,11,18,25,32,……或n=3,10,17,24,31,……,所以c9=312=961.
(方法二)令am=bn,即7m+2=n2,当n=7k+0时,bn=(7k+0)2=7·7k2不符合;当n=7k+1时,bn=(7k+1)2=7(7k2+2k)+1不符合;当n=7k+2时,bn=(7k+2)2=7(7k2+4k)+4不符合;当n=7k+3时,bn=(7k+3)2=7(7k2+6k+1)+2符合;当n=7k+4时,bn=(7k+4)2=7(7k2+8k+2)+2符合;当n=7k+5时,bn=(7k+5)2=7(7k2+10k+3)+4不符合;当n=7k+6时,bn=(7k+6)2=7(7k2+12k+5)+1不符合;所以n=3,10,17,24,31,……或n=4,11,18,25,32,……,所以c9=312=961.