低耦合度半对称三平移并联机构拓扑设计与运动学分析
2019-04-01沈惠平赵一楠许正骁杨廷力
沈惠平 赵一楠 许正骁 李 菊 杨廷力
(常州大学现代机构学研究中心, 常州 213016)
0 引言
三自由度三平移(3T)机构为国内外学者研究较多的一类机构,这类机构具有结构简单、有效工作空间大、动态性能好等优点,在工程中有较好的应用价值。CLAVEL[1]发明了著名的三维平移Delta机构,之后一些学者研究了Delta机构的衍生操作手[2-4];TSAI等[5-6]提出了一种移动副驱动、支链含4R平行四边形机构的三自由度移动并联机构;文献[7-8]对3-RRC三平移机构进行了运动学和工作空间分析;KONG等[9]提出了一种三自由度3-CRR机构,该机构具有良好的运动性能,且没有明显的奇异位置;LI等[10-11]提出了3-UPU型三平移机构,并对该机构的瞬时运动性能进行了分析;李仕华等[12]提出了一种新型3-RRUR三平移并联平台机构;陆晶等[13]提出了一种3-RRRP(4R)三平移机构,并对机构进行了运动学和工作空间的分析;谢俊等[14]提出一种以三平移全解耦并联机构为主体的茶叶筛分机,并对机构的运动学和解耦性进行了分析;ZENG等[15-16]设计了一种三平移tri-pyramid并联机构,并对其位置方程的正反解、雅可比矩阵和各向同性等运动学特性进行了分析;PRAUSE等[17]对多种三平移并联机构分别进行了数综合、边界状况和工作空间等特征的比较,选出了性能较好的机构;MAHMOOD等[18]提出了一种三自由度3-[P2(US)]机构,并对机构进行了运动学和灵巧度分析;杨启志等[19]设计了一种三平移并联移栽机器人,并对其进行了运动误差分析。
本文根据基于方位特征(Position and orientation characteristics, POC)方程的并联机构拓扑设计理论[20-21],设计一种低耦合度三平移并联机构3Pa+2RSS,并对其位置正逆解、奇异位形、工作空间及其内部奇异区域等进行分析。
1 机构设计与拓扑分析
1.1 机构设计
根据基于方位特征(POC)方程的并联机构拓扑设计理论[15],设计的机构简图如图1所示。
机构动、静平台由3条支链连接,其中,混合支链Ⅰ由3个4R平行四边形机构串联而成,从静平台0到动平台1相连的平行四边形RaiRbiRciRdi(i=1、2、3)分别记为①、②、③;其中,平行四边形①、②共面连接后,与平行四边形③垂直连接。显然,此时平行四边形②的输出杆上S点的POC集为两平移(2T),而平行四边形③末端输出杆上T点的POC集为三平移(3T),混合支链Ⅰ的拓扑等效结构可表示为HSOC1{P(4R)-P(4R)-P(4R)}。
而支链Ⅱ、Ⅲ为无约束支链R-S-S,其中,R21、R31转动副与静平台0相连,球副S23、S33与动平台1相连。
1.2 并联机构的拓扑分析
1.2.1机构的POC计算
并联机构的POC方程[15]为
(1)
(2)
式中MJi——第i个运动副的POC集
Mbi——第i条支链末端的POC集
MPa——机构动平台的POC集
选定动平台1上任一点为基点o′,确定支路末端构件的POC集,混合支链Ⅰ的POC集为
无约束支链Ⅱ和支链Ⅲ的POC集相同,分别为
确定动平台的POC集为

即动平台上任一点的POC集为三平移零转动(3T0R)。由此可知,机构只需一条混合支链就可实现三平移的设计要求,考虑到机构自由度为3,因此,还需要另两条各含一个驱动副的支链连接动定平台,因此,两条支链可采用R-S-S无约束支链或R-T-T支链。
1.2.2机构的自由度计算
并联机构的全周DOF公式[15]为
(3)
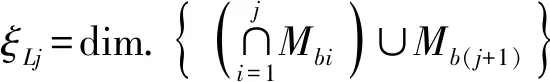
(4)
v=m-n+1
式中F——机构自由度
fi——第i个运动副的自由度
m——运动副数
v——独立回路数n——构件数
ξLj——第j个独立回路的独立位移方程数

Mb(j+1)——前j+1条支链末端构件POC集
确定由第Ⅰ、Ⅱ支链构成的第1个回路的独立位移方程数为
确定由第Ⅰ、Ⅱ支链构成的子并联机构(Sub-PM)的自由度和POC集分别为
确定由上述(Sub-PM)和支链Ⅲ构成的回路的独立位移方程数为
确定机构的自由度为
因此,该机构自由度为3,当取静平台0上的转动副Ra1、R21、R31为驱动副时,动平台1可实现3个平移的运动输出。
1.2.3机构耦合度κ的计算
由基于序单开链(SOC)的机构组成原理[15]知,任一机构可分解为约束度为正、零、负的3种有序单开链(SOC),第j个SOCj的约束度定义为
(5)
式中mj——第j个SOCj的运动副数
Ij——第j个SOCj的驱动副数
进一步,一组有序的v个SOC可组成一个零自由度的独立回路数为v的基本运动链BKC(Basic kinematics chain),对一个BKC而言,须满足
因此,BKC的耦合度为
(6)
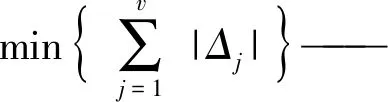
在1.2.2节中,已计算出机构两个回路的独立位移方程数,即ξL1=ξL2=6,因此,它们的约束度分别为
耦合度为
因此,该并联机构仅包含一个BKC,其耦合度κ=1,这样,机构位置正解求解时仅需建立含一个虚拟变量的非线性位置方程,并可通过一维搜索法求解该机构的位置正解。
2 机构位置分析
2.1 基于有序单开链的机构位置正解求解原理
由基于有序单开链的机构组成原理[15]可知,机构可分解为若干个BKC,而每个BKC可分解为一系列约束度分别为正值、零、负值的单开链回路,因此,机构位置正解的求解,可转换为该BKC内3种单开链回路的位置求解,而3种单开链回路的约束特性及其建模方法分别为:

2.2 位置正解求解
已知:输入角θ1、θ2、θ3,求:动平台上o′的坐标(x,y,z)。
2.2.1坐标系的建立和参数标注
机构的运动学建模如图2所示,设机构的静平台0为等边三角形,3个转动副分别位于等边三角形的内切圆的3个切点A1、A2、A3上;以静平台0的几何中心o为原点,建立笛卡尔静坐标系,x轴垂直于平行四边形①所在的平面并通过点A1,y轴平行于平行四边形①平面且指向右侧,z轴由右手法则确定。

图2 3T机构的运动学建模Fig.2 Kinematic modeling of 3T parallel mechanism
动平台1也为等边三角形,动坐标系原点o′位于动平台1的中心,x′轴垂直于C2C3,且通过G1点,y′轴与C2C3平行,指向点C2侧,z′轴根据右手法则确定。
设等边三角形静平台0的内切圆半径为a,等边三角形动平台的边长为l2;平行四边形短杆2、5、8的长度为l3,长杆3、6、9的长度为l4;平行四边形之间的连接杆4、7的长度均为l5,连接杆10的长度为l6;两条简单支链上的驱动杆11、12的长度为l7,连杆13、14的长度为l8。
A1B1与y轴负方向的夹角为θ1;A2B2与oA2延长线的夹角为θ2;A3B3与oA3延长线的夹角为θ3;D1C1与y轴正方向的夹角为δ*;F1E1与x轴负方向的夹角为γ。
易知,在静坐标系oxyz下,各点的坐标为

2.2.2Δ1>0的第一单开链回路的位置求解
在Δ1>0的回路上,设定虚拟变量δ*,而中间变量γ可通过方程求出为关于δ*的函数。
由2.2.1节知,由第Ⅰ、Ⅱ支链构成的第1回路为
{A1-B1-C1-D1-E1-F1-G1-C2-B2-A2}
易求出点C1、D1、E1、F1、G1的坐标为
(7)
同时,可计算得点o′的坐标
(8)
进一步,点C2、C3的坐标,用o′点的坐标表示为
(9)
(10)
由几何约束B2C2=l8有
整理并简化得
Asinγ+Bcosγ+C=0
令tanγ/2=u,则有
其中
A=2El4-2l4zB2

显然,γ为虚拟变量δ*的函数。
2.2.3Δ2<0的第二单开链回路的位置求解
第二单开链回路{A3-B3-C3}中:A3、B3、C3的坐标已求得,由几何约束C3B3=l8,建立位置约束方程
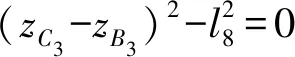
(11)
该方程中仅包含一个虚拟变量δ*,因此,可通过一维搜索,不断改变δ*的赋值,直至满足式(11)成立,获得真实的δ;再代回式(7)~(10),即可求得各个运动副位置的真实值,从而得到该机构的位置正解。计算过程如图3所示。

图3 本机构运动学正解求解流程图Fig.3 Flow chart of forward kinematics of proposed PM
2.3 位置逆解求解
已知:动平台1上o′的坐标(x,y,z),求输入角θ1、θ2、θ3。
由o′坐标(x,y,z),可求F1、E1、D1点的坐标为
(12)
由式(7)、(12),可求出γ为
另外,C2、C3的坐标已由式(9)、(10)给出,因此,由杆长条件建立位置约束方程
(13)
(14)
(15)
即可求解输入角θ1、θ2、θ3为
(16)
其中t1=l4l5-l4zD1t2=-l7zC2t3=-l7zC3

综上所述,当给定动平台1上o′的坐标(x,y,z)时,输入角θ1、θ2、θ3各有两组解,故逆解的数目为2×2×2=8,因此,机构有8种构型。
2.4 正逆解验证

由Matlab计算该机构位置正解,如表1所示。
表1位置正解数值
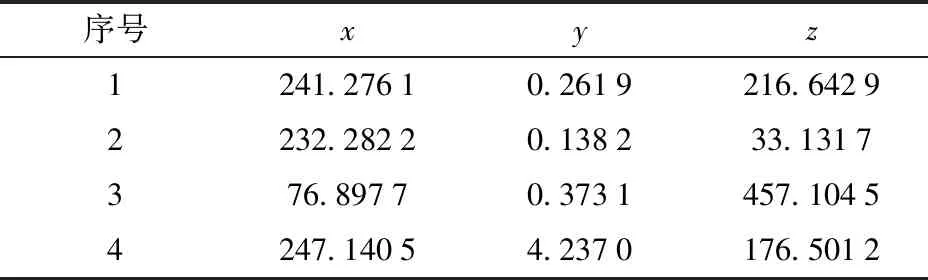
Tab.1 Numerical values of direct kinematicsmm
取表1中第3组正解数值,代入逆解式(16)中,得到θ1、θ2、θ3的8组逆解数值,如表2所示。

表2 位置逆解数值 Tab.2 Numerical values of inverse kinematics (°)
可见,表2中第3组的逆解数据和正解求解时给定的3个输入角一致,其最大相对误差为0.55%;同样,用表1中的其他正解数据,也验证了正、逆解公式的正确性。
3 机构奇异性分析
3.1 雅可比矩阵


(17)
其中
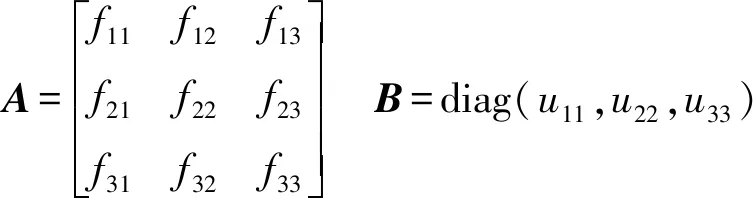
f11=xD1-xC1f12=yD1-yC1f13=zD1-zC1
f21=xC2-xB2f22=yC2-yB2f23=zC2-zB2
f31=xC3-xB3f32=yC3-yB3f33=zC3-zB3
u11=-(yD1-yC1)l4sinθ1-(zD1-zC1)l4cosθ1
u22=-(xC2-xB2)l7sinθ2/2+(yC2-
u33=-(xC3-xB3)l7sinθ3/2-(yC3-
3.2 奇异性分析
依据矩阵A、B是否奇异,将机构奇异位形分为如下3类[22]:
(1)第Ⅰ类奇异,即
detB=0
(18)
这种类型的奇异位形发生在并联机构的工作空间边界或者位置逆解数目发生变化时的位形,称为串联奇异(边界奇异)。当机构发生第Ⅰ类奇异时,机构的执行构件将失去某个方向的运动能力,此时,至少有一个运动链达到了工作空间的边界。
根据式(18)有,u11u12u13=0,所以u11、u12、u13中至少有一个为零,当u11=0,即tanθ1=-(zD1-zC1)/(yD1-yC1),即点C1、D1所在直线斜率和角θ1的斜率相等,即当Rd2Ra2和Rd1Ra1平行时如图4a所示。

图4 第Ⅰ类奇异位置Fig.4 The first kind of singularity
同理u22、u33为零的条件分别为
tanθ2= -(zC2-zB2)/(xC2-xB2)cos60°+
(yC2-yB2)cos30°
tanθ3= -(zC3-zB3)/(xC3-xB3)cos60°-
(yC3-yB3)cos30°
对应的条件分别为点C2、B2、A2和点C3、B3、A3分别在A2oz和A3oz平面共线,两个条件中,其中一个发生即为串联奇异的第2种情况。机构的2条RSS支链是对称的,因此,图4b为其中一种情况,即一条支链达到工作空间边界的情况。
当机构处于以上任一位置时,均会发生奇异。
(2)第Ⅱ类奇异,即
detA=0
(19)
这种类型的奇异位形发生在并联结构的工作空间内部,称为并联奇异(内部奇异)。此时固定并联机构的输入驱动关节,末端执行器仍存在瞬时运动,表明机构至少获得一个瞬时自由度,这时并联机构失去刚度,无法承受任何承载。
由式(19)可知,将矩阵A看作3个行向量,即:A=[e1e2e3]T,detA=0存在两种情况:
①2个向量线性相关
设ke1=e2(即e1、e2线性相关)
k(f11,f12,f13)T=(f21,f22,f23)T
即杆Rc2Rb2和杆S23S22在空间内平行,如图5a所示。
设ke2=e3(即e2、e3线性相关)
k(f21,f22,f23)T=(f31,f32,f33)T
即杆S33S32和杆S23S22在空间内平行,如图5b所示。
②3个向量线性相关
设e2=k1e1+k2e3(k1k2≠0),则有
k(f21,f22,f23)T=k1(f11,f12]f13)T+k2(f31,f32,f33)T
通过Matlab计算表明,该种情况下k1、k2的解无法解出,因此,此种情况不存在。
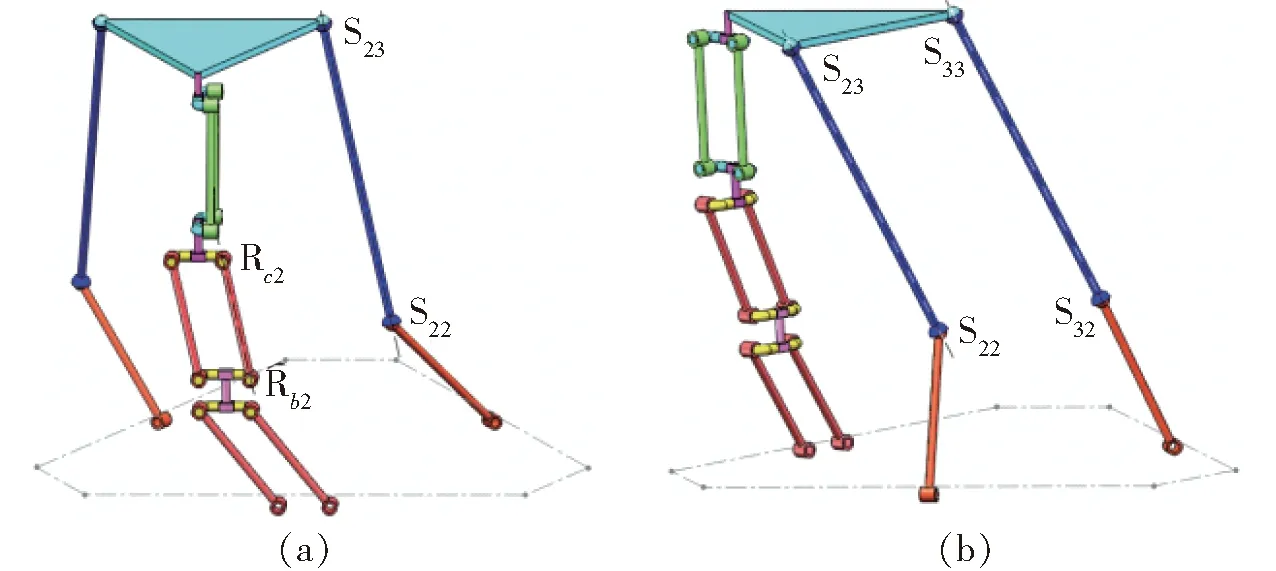
图5 第Ⅱ类奇异位置Fig.5 The second kind of singularity
(3)第Ⅲ类奇异,即
detA=0且detB=0
此时机构的驱动关节和末端执行器都存在着瞬时互不影响的非零输入和输出,对应的位姿就是第Ⅲ类奇异,处于该类奇异时,机构将失去自由度,在机构设计阶段应予以避免。
4 机构的工作空间以及内部奇异分析
U副在实际中应用广泛,相比于S副有着更大的转动范围,且结构更简单。因此,两条RSS无约束支链,实际制作时采用RUU支链,自由度、输出和运动学分析不变,但被动副的运动范围增加了很多,因此,工作空间大大增加。根据实验室已经制作的使用RUU支链替代RSS支链的样机的尺寸比例,在SolidWorks中设计虚拟样机如图6所示,在每一个U副上建立空间直角坐标系uiviwi(i=1,2,3,4),向量ai(i=2,3)表示平行于驱动副转动轴线并指向静坐标系x轴正方向的向量;向量bi(i=2,3)表示与驱动臂平行,并指向被动U副的向量。

图6 虚拟样机设计Fig.6 Virtual prototyping design

图7 被动副U22建模Fig.7 Modeling of passive joint U22
图7为支链Ⅱ中连接主动臂和从动臂的U副U22的建模图,αu1为向量n1绕着向量u1轴转动,距向量w1轴产生的偏角;αv1为向量n1绕着向量v1轴转动,距向量w1轴产生的偏角;在虚拟样机中调试动平台运动,得到向量u1和向量n1的夹角范围为30°≤arccos(u1n1) ≤120°,向量v1和向量n1的夹角范围为0°≤arccos(v1n1)≤180°。
图8为支链Ⅱ中连接从动臂和动平台的U副的U23建模图,αu2为向量n2绕着向量u2轴转动,距向量w2轴产生的偏角;αv2为向量n2绕着向量v2轴转动,距向量w2轴产生的偏角;在虚拟样机中调试动平台运动,得到向量u2和向量n2的夹角范围为50°≤arccos(u2n2)≤150°,向量v2和向量n2的夹角范围为90°≤arccos(v2n2)≤180°。

图8 被动副U23建模Fig.8 Modeling of passive joint U23
另一条RUU支链建模同理。
机构的工作空间分析,采用离散化空间三维搜索法,将搜索范围设定为:-100 mm≤x≤300 mm,-400 mm≤y≤400 mm,-450 mm≤z≤650 mm,-π≤θ≤π。
通过Matlab求得工作空间,如图9所示。

图9 工作空间及其奇异情况Fig.9 Workspace and singularities
串联奇异可以通过实际控制手段避开,因此,本文主要讨论并联奇异,即第Ⅱ类奇异。根据第Ⅱ类奇异判别式(19),利用Matlab软件编程求解,得到如图9所示的机构工作空间的三维立体图,其中,红色的点为发生第Ⅱ类奇异时在工作空间内的位置,绿色部分为无奇异区域。图10为4个x-y截面随着z值的改变奇异与非奇异工作空间情况,表明该工作空间内部的无奇异工作空间较大。
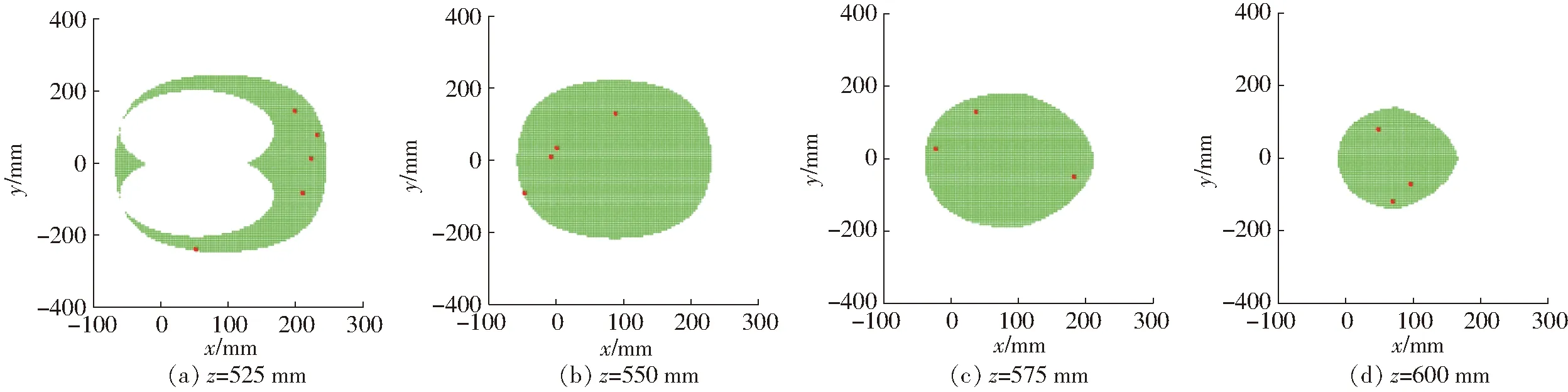
图10 工作空间内不同x-y截面内奇异情况Fig.10 Singularities in workspace from different x-y sections
5 结论
(1)提出了一种低耦合度三平移并联机构,其结构简单,具有单一动平台,可实现较大范围的三维移动。
(2)机构耦合度κ=1,因此,其位置正解求解仅需建立含一个虚拟变量的非线性约束方程,并用一维搜索法即可求得。
(3)给出了该机构发生奇异位置的几何条件和工作空间内奇异产生的位置,表明机构的有效工作空间较大。
