三元组描述符的特征匹配算法

沈学利 陈鑫彤

1(辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)2(辽宁工程技术大学研究生院 辽宁 葫芦岛 125105)

0 引 言

基于局部特征的图像匹配是图像拼接、水印嵌入、SLAM系统、三维重建等的主要步骤，是计算机视觉的一个热门研究方向。常见的匹配方法按照描述符的类型不同可分为两大类：二进制描述符、非二进制描述符。

非二进制描述符主要有：尺度不变SIFT(Scale Invariant Feature Transform)[1]的特征点检测和匹配算法，其匹配效果较好，但匹配速度较慢，算法复杂度高。加速鲁棒性算法SURF(Speeded UpRobust Feature)[2]的特征点提取与匹配，其复杂度比SIFT算法低、鲁棒性好，但相较于二进制描述符匹配速度太慢。文献[3]在SIFT算法上进行改进的ASIFT算法，仅考虑了仿射空间中图像特征点提取和匹配，对具有大视差的匹配图像具有很强的鲁棒性，但并不适合对实时性要求较高的情景。文献[4]提出的“风”(AKZE)算法，率先提出搭建非线性金字塔以更好地保护图像边缘信息，使得构建的描述符的鲁棒性增加，但搭建的非二进制描述符维度过高匹配速度较慢，匹配的鲁棒性太差，不适用对实时性和鲁棒性要求较高的场景。

针对KAZE算法和AKAZE算法搭建描述符匹配速度较慢、鲁棒性较差等问题，本文提出三元组[10]描述符与KAZE/AKAZE算法相结合的算法，可命名为KAZE/AKAZE-LATCH算法。经实验表明：KAZE-LATCH算法的鲁棒性和匹配速度都远优于KAZE算法，AKAZE-LATCH算法的整体性能相较AKZE算法有大幅度提高，AKAZE-LATCH算法鲁棒性和速度都优于KAZE-LATCH算法。

1 KAZE/AKAZE算法

1.1 非线性金字塔搭建

非线性尺度空间的构建主要基于非线性扩散滤波原理。依据非线性扩散滤波原理，KAZE/AKAZE算法与物理学中二维热扩散过程描述相似，将图像亮度视为能量，亮度随尺度变化模拟热传导流动，通过热流扩散过程函数描述图像亮度扩散。公式如下：

(1)

式中：div和▽L分别表示散度和梯度，函数c(x,y,t)表示扩散的传导函数，该函数的引入使得扩散能够适应图像局部特征，其中参数t为尺度参数，t越大，图像表示形式越简单。传导函数主要由梯度幅值控制，可变传导函数如下：

c(x,y,t)=g(|▽Lσ(x,y,t)|)c(x,y,t)=g(▽Lσ(x,y,t))

(2)

式中：▽Lσ为图像经高斯平滑之后的梯度，g是扩散函数，本文中为保留较大宽度区域，选取g为：

(3)

式中：参数k表示控制扩散对比度因子，边缘信息保留量与参数k成反比，比值越大，同一点位置相对扩散越小。式(1)为非线性扩散偏微分方程，在KAZE算法中通过AOS(Additive Operator Splitting)算法[12]求解，采用隐式差分格式，对式(1)进行离散变换，可得：

一个黑社会组织，之所以能够作恶近20年，得益于背后的“保护伞”——无为县法院刑事审判庭原副庭长吴业平。据周帮海供述，吴业平有“能量”。七年前，周帮海的“马仔”吴克任犯下两起寻衅滋事与两起故意伤害案件，他向吴业平送上2万元并请求轻判。在“吴庭长”的操纵下，身负四起情节严重案件的吴克任，仅被判处缓刑2年。连吴业平自己都说：“像这样的案子判缓刑，在法院还从来没有过。”

(4)

式中：Al是i尺度上图像亮度Li在维度l上的传导矩阵，τ为步长，m为L的行列乘积，i为图像序列。Al由式(4)可求解出Li+1为:

Li+1=(I-τ∑Al(Li))-1Li

(5)

式中：I为单位矩阵，此方法对任意时间步长τ都绝对稳定。

在AKAZE算法中，式(1)利用FED算法解非线性扩散偏微分方程，FED算法比AOS算法速度更快、精度更高。FED算法可表示为：

Li+1,j+1=(I+τjA(Li))Li+1j=0,1,…,n-1

(6)

式中:I表示单位矩阵；A(Li)为图像Li的传导矩阵；n表示显性扩散步数；τj表示对应步长，可表示为：

(7)

KAZE/AKAZE算法构建非线性尺度空间过程，是通过指数步长的系列组合生成(O个组，S个层)来离散化尺度空间，利用组索引值O和层索引值S分别识别不同的组和层，组、层与尺度参数δ的关系如下：

(8)

式中:δ0代表基本尺度，O表示组序号，S表示层序号。

因为非线性扩散滤波模型构建的尺度空间以时间为单位，所以将以图像像素为单位的尺度参数转化成以进化时间为单位的尺度参数。在高斯空间中，使用标准差为δ的高斯卷积，相当于图像进行时间t=δi/2的滤波。由此可知尺度参数δi与进化时间t之间的映射关系为：

(9)

KAZE/AKAZE算法构建尺度空间的流程是：首先通过高斯卷积平滑处理图像，减小噪声和形变等干扰；然后计算图像梯度直方图，以获取对比度因子参数k，确定保留边缘信息量；最后用进化时间序列构造非线性尺度空间，并且通过AOS算法或者FED算法及简单迭代求解，获取到非线性尺度空间图像序列：

(10)

1.2 KAZE/AKAZE特征点定位

AKAZE/KAZE算法使用Hessian矩阵在非线性金字塔上寻找极大值从而确定特征点，如下式：

(11)

式中：σi为尺度因子初始值，Lxx、Lyy和Lxy分别表示x方向，y方向和xy方向的2阶导数。对于每一个经过hessian矩阵归一化的像素点，将其与金字塔相邻尺度中σi×σi区域以及本身所在尺度σi×σi区域的像素点进行比较，求取区域特征点。

定位特征点的位置，以特征点为中心，画出半径为σi的圆分为6个扇形，如图1所示。计算每个扇形内所有像素点在水平和竖直方向的一阶导数的高斯加权值，高斯加权值最大方向即为特征点的主方向。

图1 特征点方向

2 KAZE/AKAZE-LATCH描述符建立

前面对KAZE/AKZE算法非线性金字塔发搭建、特征点定位、特征点的方向，进行了详细的叙述，在本节中需要对描述符的建立进行详细的阐述。传统的二进制描述符如：BRIFE、BRISK等都是根据两像素之间的关系建立描述符，这种描述符的鲁棒性较差，易受光照、尺度、噪声等的干扰，导致匹配效果较差。故在本文中提出AKAZE/KAZE-LATCH算法，利用LATCH算法建立三像素之间的关系建立描述符。

如图2所示，假设以特征点为中心的采样窗口内有p1、p2、p3三个像素块，每个像素块中包含m×m个像素，比较两个像素块与对应位置像素块的平方和，可表示为：

(12)

则LATCH描述符可表示为：

(13)

图2 三元组描述符

选择24σi×24σi采样区域建立描述符，原LATCH描述符选择确定的m×m像素块建立关系，为了使LATCH描述符具有更强的尺度不变性，本文提出根据尺度关系建立像素块，像素块尺寸为3σi×3σi。若像素块尺寸为非整数，则使用双线性差值算法计算像素块的像素值，如图3所示，可表示为：

(14)

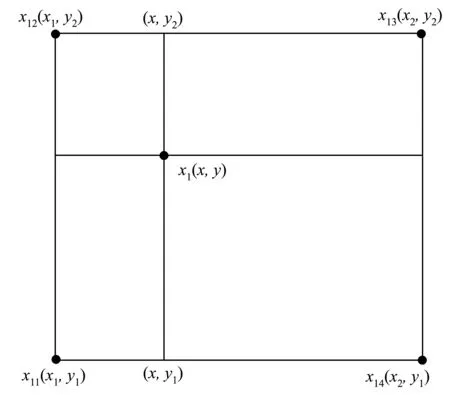
图3 双线性差值算法

3 实 验

3.1 实验过程

为了验证所提算法的优越性，选择SIFT算法、ORB算法、AKAZE算法、KAZE算法等四种具有代表性的基于局部特征的匹配算法，在INRIA数据[13]中具有模糊变换、光照变换、视角变换和JPEG变换的图像进行对比实验。

其中SIFT算法的描述符为非二进制，并且为最经典的匹配算法；ORB算法描述符是二进制描述符，在众多二进制匹配算法中效果最佳；本文算法是在KAZE算法和AKZAE算法的基础上进行改进。故选择了上述四种算法进行对比实验。

本文实验实验平台为个人笔记本，匹配AMD-A84-500、4 GB内存，基于Opencv 3.10在Visual Studio 2013上进行实验。

3.2 实验结果

在本文实验中SIFT算法为128维描述符；ORB算法的二进制描述符为256 bit；KAZE算法的描述符为64维；AKZAE的描述符为256 bit；本文所提算法描述符为256 bit。

图4为基于局部特征图像匹配的评价图像，每一组6张图像，第一张为基准图像，剩余的五张为待匹配图像，随着同组图像编号的增加图像变化程度增加。如图4所示，(a)和(b)为图像模糊变换，(c)和(d)为图像JPG压缩，(e)和(f)为具有视角差的wall图像，(g)和(h)图像为光照发生变换。

(a) Bike图像(1/6) (b) Bike图像(6/6)

(c) BUC图像(1/6) (d) UBC图像(6/6)

(e) wall图像(1/6) (f) wall图像(6/6)

(g) Leuven图像(1/6) (h) Leuven图像(6/6)图4 图实验图像

3.3 实验分析

KAZE算法率先提出了使用非线性金字塔有效地保护了图像边缘信息，利用加速鲁棒性算法SURF(Speeded Up Robust Feature)的思想建立描述符，使得KAZE算法的鲁棒性进一步增加，故匹配正确率优于SIFT算法。AKAZE算法使用精度更高、速度更快的FED算法解非线性函数，LDB二进制描述符不仅计算了像素块之间的强度关系还表达了梯度关系，使得描述符的鲁棒性大大增加，故相对于KAZE算法正确率得到极大提升。SIFT算法为最为经典的匹配算法，采用128维梯度描述符，搭建的高斯差分金字塔使得描述符的鲁棒性不及KAZE算法，但仍然优于二进制描述符ORB算法。ORB算法描述符为二进制描述符，通过比较特征区域中像素值大小建立描述符，故ORB算法的鲁棒性最差。本文所提的KAZE-LATCH算法，使用非线性金字塔一方面增加描述符的鲁棒性，另一方面计算三个像素块之间的信息建立描述符，使得二进制三元组描述符的鲁棒性进一步增加，故匹配正确率相较于KAZE/AKAZE算法有巨大提升。AKAZE-LATCH算法的利用FED算法搭建的非线性金字塔精度更高，LATCH描述符的鲁棒性相较于LDB算法的鲁棒性更强，故AKAZE-LATCH算法匹配正确率要优于AKAZE算法和KAZE-LATCH算法。

图5为SIFT算法、ORB算法、KAZE算法、AKZE算法、KAZE-LATCH算法和AKAZE-LATCH算法对具有模糊变换、光照变换、视角变换和JPEG变换的图像进行匹配时，匹配正确率的统计。由图5(a)折线图分析可得，在模糊变换情境中，匹配正确率由大到小排序为：AKAZE-LATCH算法、AKAZE算法、KAZE-LATCH算法、KAZE算法、SIFT算法、ORB算法对于具有模糊图像致使描述符的鲁棒性下降，二进制描述符的稳定性虽不及非二进制描述符，但AKAZE-LATCH算法本身具有很大的优势，故匹配正确率最高。由图5(b)可得，在具有JPEG变换图像中，匹配正确率顺序排列为：AKAZE-LATCH算法、AKAZE算法、KAZE-LATCH算法、KAZE算法、ORB算法、SIFT算法。JPEG压缩致使图像的信息丢失，利用局部梯度建立的描述符的鲁棒性会严重下降，故SIFT算法的匹配正确率最低。由图5(c)可得，在具有视角差图像中，匹配正确率顺序排列为：AKAZE-LATCH算法、KAZE-LATCH算法、AKAZE算法、KAZE算法、SIFT算法、ORB算法。由图5(d)可得，在具有亮度变换图像中，匹配正确率顺序排列为：KAZE算法、AKAZE-LATCH算法、KAZE-LATCH算法、AKAZE算法、SIFT算法、ORB算法。

(a)

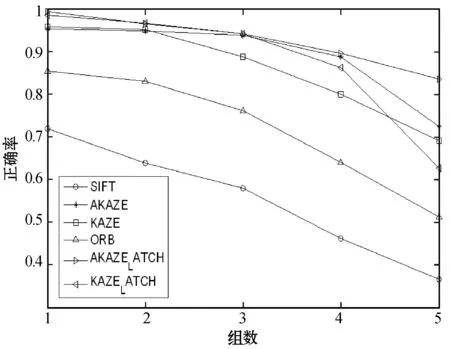
(b)

(c)

(d)图5 匹配正确率

由表1可以得到匹配速度顺序排列为：KAZE-LATCH算法、AKAZE算法、ORB算法、KAZE-LATCH算法、KAZE算法、SIFT算法。由于二进制描述符使用汉明距离计算相似度，比非二进制描述符匹配速度快，故SIFT算法和KAZE算法匹配速度较慢。AKAZE算法的非线性方程由速度更快的FED算法计算，故匹配速度远超过KAZE算法。而LATCH描述符根据三个像素的关系确定描述符，相对于LDB描述符需要计算梯度，速度上进一步提升，故AKAZE-LATCH算法速度快于AKAZE算法。KAZE-LATCH算法与AKAZE-LATCH算法相比，虽描述符种类相同，但FED算法计算速度要优于AOS算法，故KAZE-LATCH算法匹配速度不及AKAZE-LATCH算法。ORB算法只需要搭建高斯金字塔，特征点检测速度也较快，描述符又为二进制，故匹配速度最快。

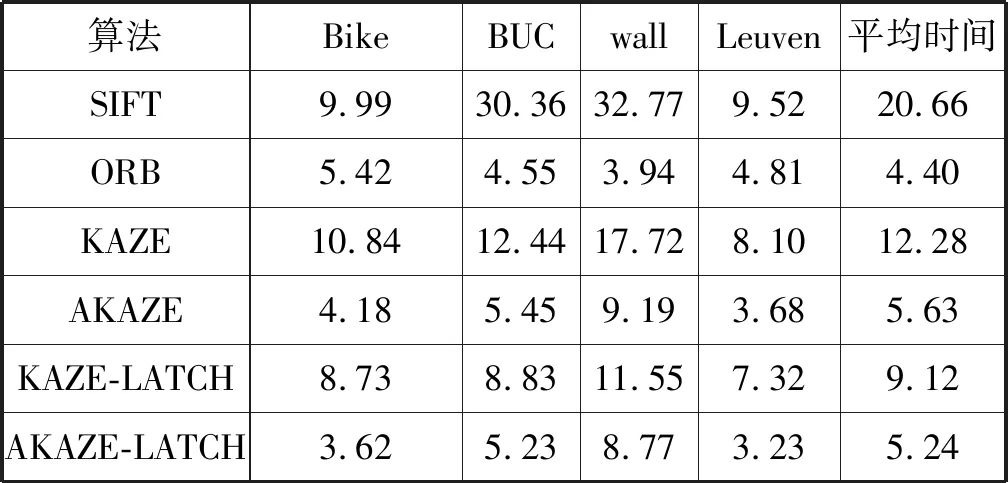
表1 匹配时间 s

4 结 语

针对KAZE/AKAZE算法匹配鲁棒性较差、匹配速度较慢等问题，本文提出一种三元组描述符与KAZE/AKAZE结合的算法。首先利用AOS算法或者FED算法解非线性方程搭建金字塔；然后借用海森矩阵确定特征点的位置；最后根据特征点所在尺度选择相应的采样域建立三元组描述符，若是像素块非整数借助双线性插值计算。实验结果表明：AKAZE-LATCH算法比原AKAZE算法匹配正确率提升10%，运行速度提升7%；KAZE-LATCH算法比原KAZE算法匹配正确率提高15%，匹配速度仅为KAZE算法的75%，可广泛应用于对匹配速度和精度要求较高的场景。