改进TOPSIS法用于出租房源综合评价研究

邓璐娟 陈欣欣

1(郑州轻工业学院软件学院 河南 郑州 450002)2(郑州轻工业学院计算机与通信工程学院 河南 郑州 450002)

0 引 言

网上出租房源信息冗乱繁杂，很难进行比较和评价，研究一种改进的TOPSIS法对网络爬虫抓取的出租房源进行综合评价，评价结果以地图图标的形式推送给对出租房源属性侧重点需求不同的租房者，为亟待租房的对象提供了有价值的服务。

逼近于理想解排序TOPSIS法是按照各评估对象到理想化目标的接近程度对有限评估对象进行相对优劣选择的方法，常被用于多属性多目标排序的场景，其主要优势是简单、计算量小、几何意义直观、便于理解和运用等[1-4]。然而，因传统TOPSIS方法中欧式距离本身的局限性，导致运用其进行综合评价时可能会出现两点不足：① 当评估对象的属性线性相关时，欧式距离失效；② 当评估对象距离正负理想解等同远近时，不能完全反映其对象的位置关系[5]。近年来，纵观国内外对于传统TOPSIS方法的改进，一些专家专注于传统TOPSIS法的决策环境的拓展研究，一部分注重欧式距离权重确定方面的完善，还有一部分学者仅仅对传统TOPSIS方法的缺陷做了相应改进[6]，均没有同时解决利用传统TOPSIS法排序的两个缺陷。本文对出租房源评价应用中，其评估对象的面积、租金属性之间显然存在相关性及位置不确定性，一般TOPSIS法无法合理地对各个出租房源的优劣性进行判定。故而研究一种既能解决出租房源属性(面积、租金、间隔目标点距离)间线性相关问题，又能解决出租房源间隔正负理想解等同距离时无法准确定位的问题的改进TOPSIS法对出租房源进行合理的排序势在必行。

1 TOPSIS方法

TOPSIS法是通过计算待评估对象的各个属性指标与正反理想解的距离尺度，求得与理想解的相应贴近值，进而对评估对象进行评价的一种综合排序法[7-8]。用TOPSIS法对出租房源评价的数学模型如下：

(1) 构建出租房源信息矩阵:

如矩阵A所示,表示出租房源的第j个属性指标值，本文具体指出租房源的面积、租金和间隔目标点的距离。

(2) 数据标准化处理:

(1)

(2)

式(1)将成本型属性指标(出租房源的面积属性)归一化为取值范围在[0,1]之间效益型指标数据;式(2)对出租房源信息矩阵中所有属性数据进行标准化处理，如A′所示:

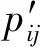
(3) 特征矩阵权重规范化:

对出租房源进行综合评价时，鉴于不同用户对属性指标偏重不同，如何给各个属性指标赋予权重成为了利用TOPSIS法排序的关键问题之一。权重赋值方法很多，本文通过比较其优劣性，选择信息熵对各个属性进行权重赋值，信息熵越小，表示其透露出来的信息量较大;反之，表示其透露出来的信息量较少[9]。对特征矩阵熵权重规范化的基本步骤如下：

(a) 计算出租房源各属性指标的熵值，其公式如下：

(3)

(4)

(5)

(b) 对各出租房源属性指标熵权重化，其公式如下所示，其中i=1, 2,…，n。权重规范化后的特征矩阵如A″所示。

vij=wj×Pij′

(6)

(4) 确定正理想解和负理想解:

正理想解代表不同出租房源的同一属性指标中的最大值，而负理想解则代表不同出租房房源中同一属性指标中的最小值。其公式如下：

(7)

(8)

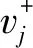
(5) 计算距离尺度:

计算各出租房源属性指标值间隔正反理想解的距离尺度：

(9)

(10)

(6) 计算与正反理想解的贴近值:

计算各出租房源与理想解的相应贴近程度：

(11)

(7) 对出租房源方案进行排序:

2 TOPSIS方法的改进

2.1 马氏距离改进TOPSIS法

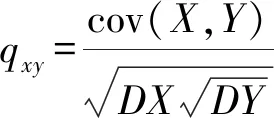
(1) 构建原始信息矩阵A，因马氏距离不受属性间相关性和量纲的影响，故不需要对A进行规范化处理，省略掉了传统方法模型中的第2步。马氏距离的权重是内化于公式之内的客观赋权，故省掉了传统方法模型中的第3步。

(2) 确定正负理想解。假定Bi=(bi1,bi2,…,bin)是第i个出租房源所对应属性的空间坐标，S+={s+1,s+2,…,s+n},表示负理解所对应的空间坐标,S-={s-1,s-2,…,s-n}对于本文爬取的郑州市的出租房源，Bi的坐标是变化的，正负理想解S+与S-的坐标是固定的,Σ-1表示n个属性变量b1,b2,…,bn的相关系数Σ的逆矩阵。则第i个评估对象Bi到S+与S-的马氏距离，如下式所示：

(12)

(13)

(3) 计算各出租房源的相对贴近度。计算爬取的郑州市的各出租房源到正负理想解的S+与S-的贴近度。其贴近值计算方法如下：

(14)

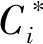
2.2 最差理想解改进TOPSIS方法

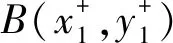
图1 最差理想解图

(15)

(16)

(17)

2.3 结合马氏距离与最差理想解改进TOPSIS方法

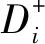
(18)

(19)

式中：α、β代表租房者偏好系数，且α+β=1，求解各出租房源的相对贴近度Ci，公式如下：

(20)

式中：Ci∈[0,1],Ci值越大，代表出租房源排序结果性能越优，排序顺序越靠前。将马氏距离和最差理想解相结合对传统TOPSIS法的改进，涵盖了两者单独改进TOPSIS法的优良特性，既解决了评估对象间隔正负理想解等同距离的问题，又消除了欧氏距离本身局限性导致的出租房源属性之间相关性的影响。

3 出租房源综合评价

本文将爬虫系统爬取的某两大租房网站的郑州市出租房源信息作为评估对象，以郑州大学为目的地，将出租房源的面积属性作为效益型指标，租金和根据经纬度求得的距离属性作为成本型指标，利用传统TOPSIS法和改进后TOPSIS法分别对其进行综合排序实现。

3.1 传统TOPSIS方法出租房源评价

利用传统TOPSIS法对爬虫系统爬取的某两大租房网站的12 000多条郑州市出租房源进行综合排序，根据上述传统TOPSIS法模型中式(1)-式(4)求得待评估出租房源的面积、租金、距离属性权重级w={0.060 7,0.763 4, 0.483 3}。根据式(6)、式(7)求得各出租房源的正负理想解为：

v+=[0.008 5 0.195 2 0.030 0]

v-=[0.002 0 0.050 0 0.011]

根据式(9)-式(11)求得各出租房源的相应贴近度，其综合排序结果的前10个最优出租房源及相对贴近度，如表1所示，其排序结果高德地图图标展示如图2所示。

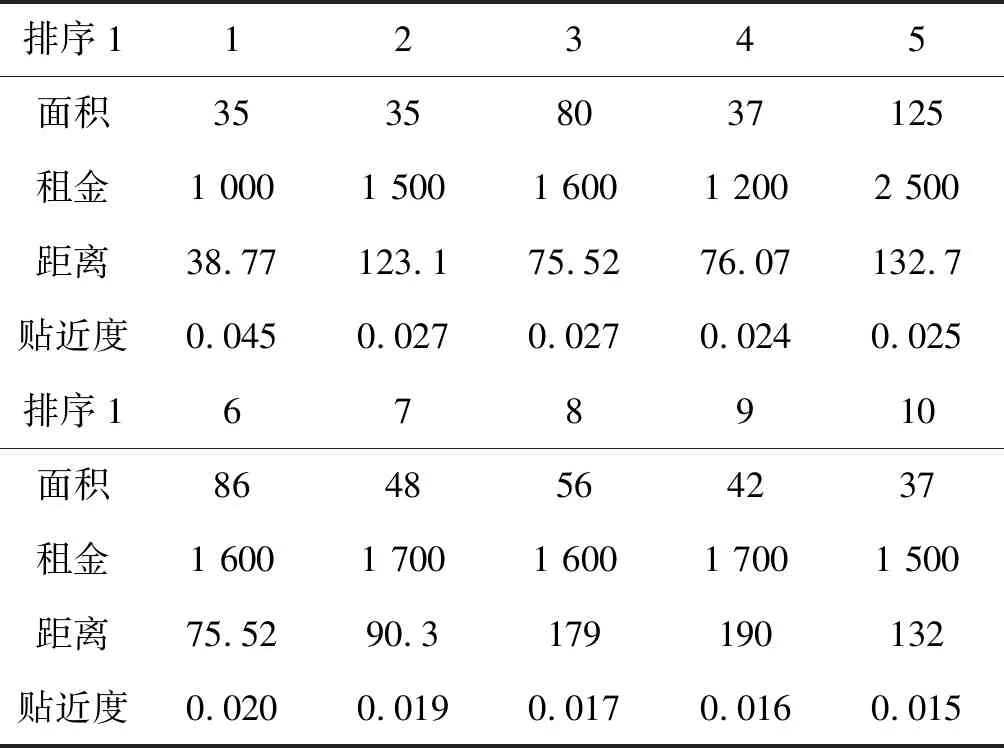
表1 传统TOPSIS法排序结果

图2为熵权重化的传统TOPSIS法对出租房源的排序效果展示图。图标1表示根据输入的目的地郑州大学和出租房源的面积、租金及经纬度求得的距离属性，利用传统TOPSIS法对爬虫系统爬取的郑州市的12 000条出租房源排序的最终评价结果中贴近度最大的出租房源(最优出租房源)，分组1表示其综合排序结果的前1～7个最优出租房源地图图标显示。

3.2 马氏距离优化TOPSIS出租房源评价

利用MATLAB对爬虫系统爬取的出租房源的面积、租金和通过经纬度信息求得的各出租房源间隔目标地点郑州大学的距离属性，求解相关系数矩阵，其结果如矩阵B所示:

由B可知，出租房源属性间存在较大的相关性，面积与租金之间的相关系数甚至达到了0.9。租金、距离的相关性系数也达到了0.5，传统TOPSIS法对出租房源评价欧式距离失效，利用马氏距离替代欧氏距离改进TOPSIS法对出租房源进行综合评价更具合理性。

根据马氏距离改进TOPSIS法模型中的式(12)-式(14)分别求得各出租房源的相应贴进度，其综合评价的前10个最优出租房源与相应贴近度如表2所示，综合评价结果高德地图图标展示如图3所示。

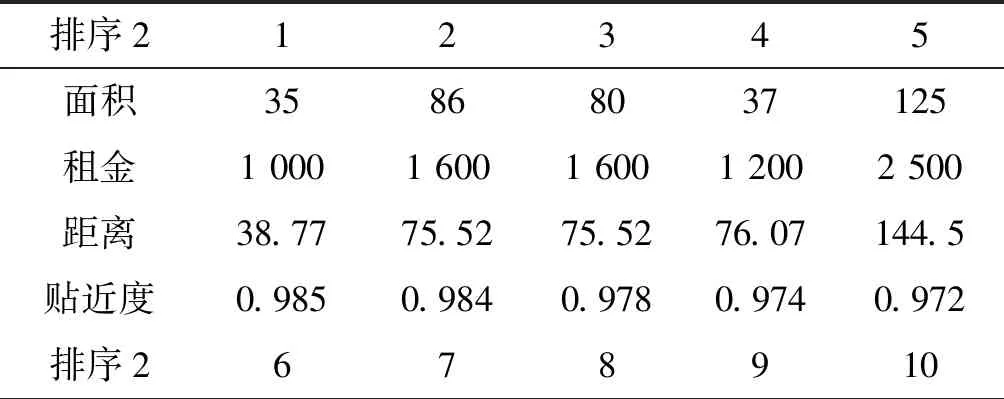
表2 马氏距离改进TOPSIS法排序结果

续表2

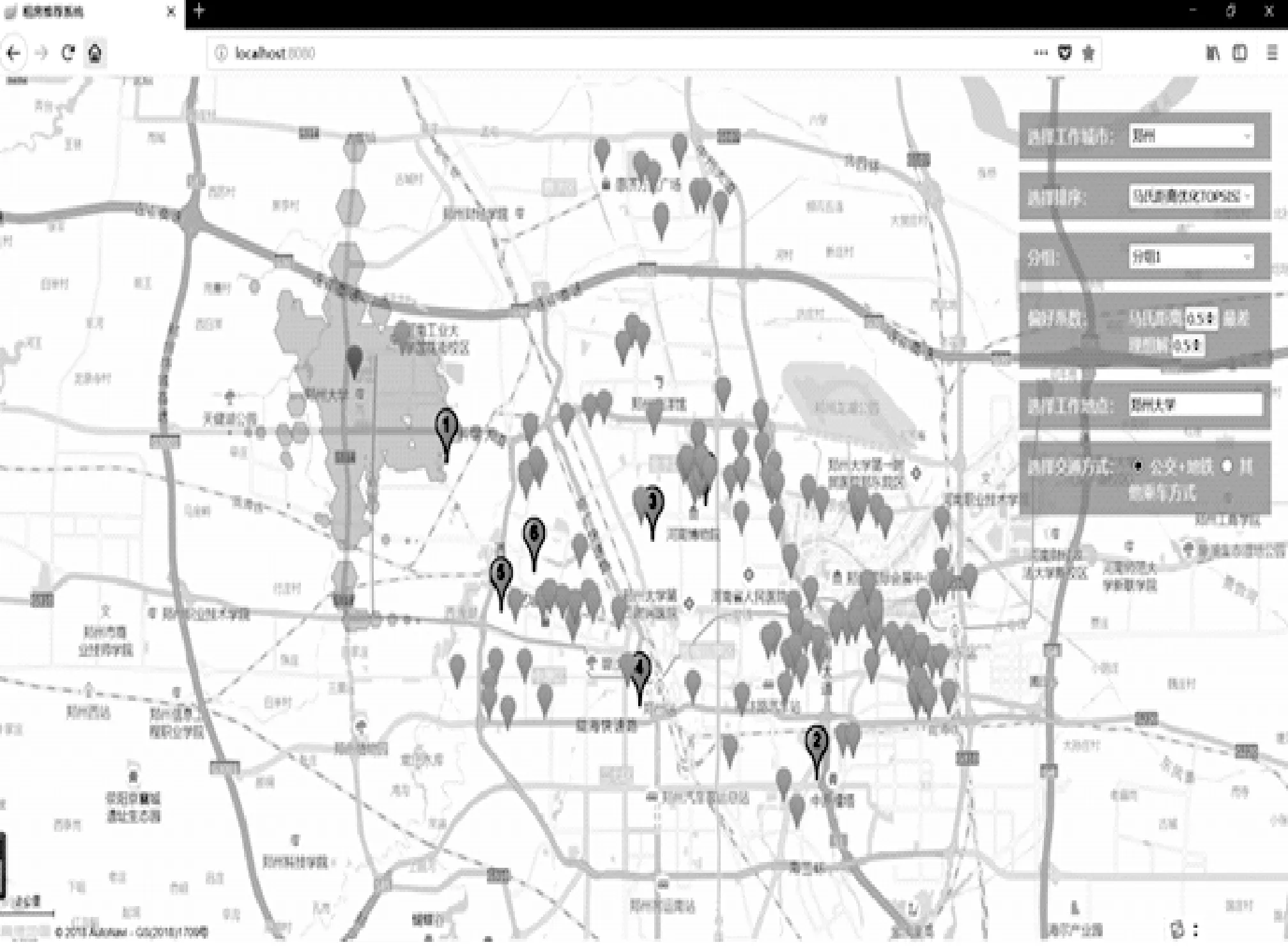
图3 马氏距离优化TOPSIS法效果图

图3为马氏距离优化TOPSIS法的排序效果展示图。图中水滴形图标表示依据输入的目的地点郑州大学和出租房源的面积、租金及经纬度求得的距离属性，利用马氏距离改进的TOPSIS法对郑州市12 000条出租房源进行综合排序的最终结果中的前200个出租房源，图标1表示根据上述排序法排序的最终综合评价结果中的最优出租房源选择，图中分组1表示综合评价结果的前1～7个最优出租房源展示。

3.3 最差理想解改进TOPSIS出租房源评价

通过爬虫系统爬取的原始出租房源数据和传统TOPSIS法求得的正、负理想解为：

v+=[0.008 5 0.195 2 0.030 0]
v-=[0.002 0 0.050 0 0.011]

根据最差理想解改进TOPSIS法模型求得最差理想解K*=[-0.004 5 -0.095 2 -0.008]，根据式(15)-式(17)求得最差理想解下的距离尺度、贴近度。其排序结果的前10个最优出租房源选择、相应距离尺度和贴近度，如D-，D*和表3所示，综合排序结果地图图标展示如图4所示。

D*=3 452 984.548 7 180 342.15 3 074 082.861

2 940 061.853 6 549 101.029 4 363 638.394

13 962.282 4 699 275.118 5 427 955.725

21 950 748.67

D+=63 293 136.32 51 792 762.34 64 577 297.98

63 130 525.87 53 363 598.8 59 551 441.88

61 375 367.95 58 610 154.64 55 445 180.23

28 223 049.91

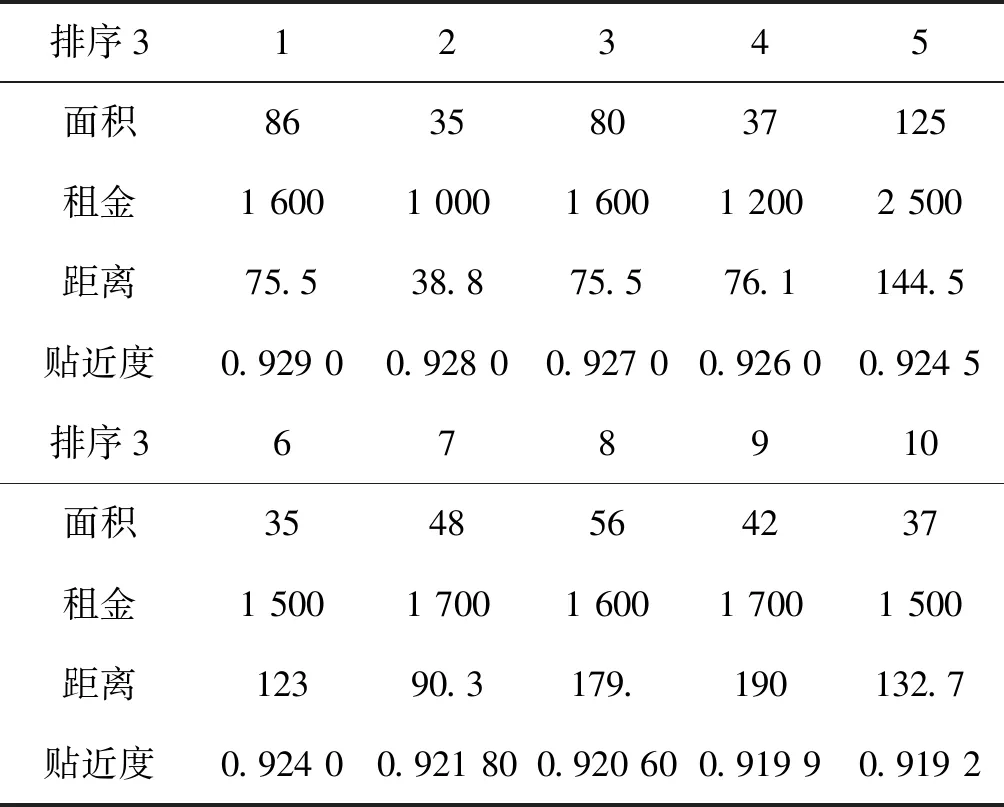
表3 最差理想解优化TOPSIS排序结果

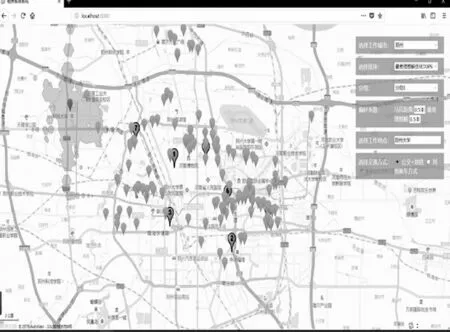
图4 最差理想解优化TOPSIS效果图

图4为利用最差理解代替负理想解优化TOPSIS法的排序效果展示图。图标1表示根据输入的目的地点郑州大学和出租房源的面积、租金及经纬度求得的距离属性，利用最差理想解改进的TOPSIS法对郑州市12 000条出租房源排序的最终综合评价结果中的最优出租房源，图中分组1表示其综合排序结果的前1～7个最优出租房源展示。

3.4 综合马氏距离和最差理想解优化TOPSIS评价

将马氏距离和最差理想解两种方式单独改进TOPSIS法所得距离尺度d(Ai，S+)、d(Ai,S-)、Di*、Di-进行无量纲化处理后代入式(18)-式(20),假设租房者对这两者的偏好度相同均为0.5，求得各出租房源的贴近度，其综合排序结果的前10个最优出租房源选择和相应贴近度，如表4所示，其最终评价结果高德地图图标展示如图5所示。

表4 马氏距离综合最差理想解优化TOPSIS排序结果

图5 马氏距离综合最差理想解优化TOPSIS法效果

图5为马氏距离综合最差理想解优化TOPSIS法排序效果展示图。图标1表示根据输入的目的地郑州大学和出租房源的面积、租金及经纬度求得的距离属性，利用最差理想解综合马氏距离改进的TOPSIS法对郑州市出租房源进行综合评价的结果中的贴近度最大出租房源。偏好者系数表示当马氏距离结合最差理想解优化TOPSIS法时，租房者根据两者优化TOPSIS法产生的作用选择的比例(总数是1)，它是可以改变的。如果租房者认为属性间的相关性对排序结果的影响较大，可以适当加大马氏距离优化TOPSIS法的比例，降低最差理解的优化TOPSIS法的比例，反之亦同。本文是以两者相同比例0.5为例，对出租房源进行排序展示的。图中分组1表示其综合排序结果的前1～7个最优出租房源展示。

4 出租房源排序结果分析

4.1 排序结果误差差异值分析

验证本文改进的TOPSIS法综合评价的性能。假定RankResult={Rank(1),…,Rank(j),…,Rank(m)}，其中Rank(j)表示排在第j个位置的评估对象。定义Diffi=((Rank(j),Rank(j′)表示第Rank(j)个评估对象和第Rank(j′)个评估对象在属性i上的评价结果与实际评价结果相违背的权重差异值，其中j

定义Error为实际评价结果与分别针对单一属性值对评估对象评价的总违背差异值，计算公式如下：

(22)

本文将Error作为评估标准，验证不同改进方式对传统TOPSIS法综合评估性能的影响，其总违背差异值Error值越小，评估性能越优。5次评价实验结果如表5所示。

表5 优化TOPSIS排序结果

本文进行了离差最大化权重化传统TOPSIS排序、信息熵权重化传统TOPSIS排序、最差理想解优化传统TOPSIS法排序、马氏距离优化TOPSIS排序、马氏距离结合最差理想解优化TOPSIS法排序共五种综合评估验证实验。根据实验结果，显然，利用离差最大化对传统TOPSIS法权重化求得的评价结果，其总违背差异值是最大的。因此，本文在对传统TOPSIS的改进中，除马氏距离使用的是其内化权重，其他方式的优化均是在熵权重化的条件下进行的，由表3比较分析可知，无论马氏距离和最差理想解两种方式单独对传统TOPSIS法的改进，还是将两者结合对TOPSIS法的改进，其评价结果的总违背差异值均有所降低。尤其是将马氏距离与最差理想解相结合优化TOPSIS法的评价结果其总违背差异值仅为9 105.942 8，显然性能最优。

4.2 排序结果数据对比分析

4.2.1 改进前后的TOPSIS对比分析

将推荐结果表1(传统TOPSIS方法)和表3(最差理想解改进TOPSIS方法)进行对比，其传统TOPSIS法排序6变成了最差理想解优化TOPSIS法的排序1，排序1变成了排序2，而排序2退到了排序6的位置。显然导致这种变化的根本因素是传统TOPSIS法对出租房源评价时，存在出租房源间隔正负理想解等同距离导致无法被准确定位的问题。而本文利用最差理想解代替负理想解优化TOPSIS法对出租房源综合排序时，很好地解决了这一问题。比较马氏距离优化TOPSIS方法所得排序结果(表3)与传统TOPSIS法所得排序结果(表1)，发现除排序1、3、5、7、8之外，其他的出租房源排序均发生了较大偏移。这是因为出租房源的属性指标(面积，租金)之间存在相关性，导致传统的TOPSIS方法对其进行评价时欧式距离失效，而马氏距离因不受量纲影响，消除了属性指标间相关性影响。将马氏距离与最差理想解相结合优化TOPSIS方法的推荐结果(表4)与传统TOPSIS法的推荐结果(表1)进行对比。发现传统TOPSIS法排序6变成了改进TOPSIS法排序2，排序4变成了排序6，排序2则倒退到了排序4的位置，排序9和10互换了位置，这种差异主要是因为最差理想解综合马氏距离优化TOPSIS法不仅解决了出租房源面积、租金等属性间相关性问题，又解决了出租房源距离正负理想解等同远近时无法准确定位的问题。

4.2.2 综合改进TOPSIS与单独改进TOPSIS对比分析

分析马氏距离综合最差理想解改进TOPSIS法的排序结果(表4)与马氏距离改进TOPSIS法(表3)可知，其结果除4和6互换了位置，其他均没太大变化。这是因为对出租房源进行综合排序时，其面积、租金等属性间相关性对出租房源的排序结果影响较大，而无论马氏距离综合最差理想解优化TOPSIS法还是马氏距离单独优化TOPSIS法对出租房源进行排序，均克服了这一缺陷。这种情况体现了改进方法对出租房源评价的一致性，表明了本文改进TOPSIS法排序的有效性。而细微的差异性则因为马氏距离改进传统TOPSIS法仅解决了出租房源面积、租金等属性之间相关性导致欧式距离失效的问题，但可能存在因出租房源距离正负理想解相同距离，导致排序无法确定位置的问题。马氏距离与最差理想解相结合改进TOPSIS法同时解决了以上两个缺陷。将马氏距离结合最差理想解改进TOPSIS方法对出租房源排序的结果(表4)与最差理想解单独改进TOPSIS法的排序结果(表2)对比，其排序1变成了排序2，排序10变成了排序9，这种差异显然是因为最差理想解单独改进TOPSIS法只是解决了出租房源距离正负理想解等同远近的问题，没有解决出租房源属性(面积、租金、间隔目标点距离)间线性相关问题。

综上所述，本文提出的将马氏距离与最差理想解相结合优化的TOPSIS方法比马氏距离和最差理想解单独改进TOPSIS方法更具有科学性及有效性，应用于对出租房源的评价也更合理。

4.3 排序结果实用价值分析

分析马氏距离综合最差理想解优化TOPSIS法对出租房源评价的结果(表4)的实用价值可知，排列在第一位的出租房源，其租金1 000、面积35、距离38.77等指标方面分配较合理，性价比最高。对于排列在第2位和第3位的出租房源，在其租金、距离属性相同的条件下，第3位出租房源的面积却比第2位出租房源的面积少了6平方米，显然将第3位排到第2位之后也合理的。而对于第3位、第4位出租房源在其距离相差不大的情况下，第4位出租房源虽租金比第3位少了400元，但其面积减少了二分之一，故排序也是合理的，对于排列在第5位、第6位、第7位的出租房源，在其距离基本差异不大的基础上，第5位出租房源的租金虽比第6位多了1 000元，而面积比第6位增加了四分之三，故其排序合理，排序在第7位的出租房源其面积虽比排列在第6位的出租房源多了10平方米，但租金却多出了200元，故将其排列在后面也是合理的。对于排列在第8位、第9位的出租房源，第9位的出租房源距离目的地点郑州大学的距离比排序在第8位少了50、但是面积却少了10平方米，故排序也是合理的。而对于排序在第10位的出租房源其面积是42平方米，距离是200，租金却高达1 700元，可见性价比比前9个出租房源都低，故把它排最后一位也是合理的。

综上所述，本文将马氏距离和最差理想解相结合优化TOPSIS方法对出租房源进行综合排序的评价结果具有合理的现实意义和实用价值。

5 结 语

本文通过研究传统TOPSIS方法的缺陷，提出了一个适用范围更广且更加合理的改进TOPSIS方法，即用马氏距离代替欧氏距离，用最差理想解代替负理想解优化传统的TOPSIS法，并将其应用到爬虫系统爬取的出租房源的多属性排序中。实验证明该方法有效地消除了传统TOPSIS法因出租房源面积和租金等属性间相关性导致的欧氏距离失效及距离正负理想解等同远近无法定位的缺陷，对出租房源的排序更具合理性及科学性，其排序结果更具实用价值和现实意义。本文的不足之处是该方法仅限于数值属性的决策分析，而对那些需要进行混合型属性分析的评估对象并不适用，故本文下一步将重点研究如何改进TOPSIS法，使其能够根据评估对象的混合属性进行综合评价。