基于边缘映射抽样与多维尺度压缩的紧凑图像哈希算法
2019-04-01戴歆杨成陈栎
戴 歆 杨 成 陈 栎
1(武汉商学院信息工程学院 湖北 武汉 430056)2(南昌大学软件学院 江西 南昌 330000)
0 引 言
随着数字信号处理的方便,多媒体内容的可靠性和可信度已成为人们普遍关注的问题,而数字图像因其具有良好的直观表达能力,已成为当前各领域中必不可少的载体,得到了广泛应用[1]。然而,近年来,随着计算机软件与理论的日益完善,相应的图像编辑工具也变得更加容易得到,攻击者能够轻易获取这些软件,对图像实施肆意修改,使得普通用户无法对其内容的可靠性完成判别,给其信息安全带来隐患[2]。对此,国内外学者设计了图像认证方案,如哈希方法,它是从短的二进制或实数序列来提取图像特征,可作为图像的惟一表示而用于其信息的真伪决策,该技术对其内容具有强烈的敏感性当图像内容发生极其微小变化,所产生的哈希值与初始图像存在巨大差异[3-4]。图像哈希序列的生成主要分为图像预处理、特征提取与哈希序列三个过程,其中,特征检测是其关键内容,其鲁棒性的高低对整个哈希算法具有重要影响[3-4]。如王彦超等[5]为了提高哈希序列对常见几何篡改的鲁棒性,提出了基于联合特征与中心方向信息的图像哈希算法。此方案对图像的特征描述较为充分,使其获得较为理想的鲁棒性,但是,从图像钟提取三种特征,且直接将其视为哈希,导致其哈希维度非常高,降低了生成效率。唐振军等[6]为了降低哈希维度,利用主成分分析机制,设计了一种紧凑哈希算法,利用插值运算与滤波器来预处理图,显著提高了哈希生成效率。但是,该方案无法充分提取图像的鲁棒特征,导致整个哈希序列的鲁棒性不理想,特别是旋转修改,其识别正确率较低。Tang等[7]为了提高哈希序列对几何变换的稳健性,利用高阶张量方法,提出一种的紧凑图像哈希方案。该哈希方案利用了Lab颜色空间转换,以去L分量为特征,充分提高了哈希对亮度修改的鲁棒性。但是,张量分解难以有效充分获取L分量的抗旋转鲁棒特征,使其对角度旋转的正确识别率不高。
为了兼顾哈希序列对几何修改的鲁棒性与生成效率,本文提出了基于边缘映射抽样与多维尺度压缩的紧凑图像哈希算法。利用预处理方法来规范图像尺寸,可消除尺度缩放对哈希序列的影响;随后,利用显著边缘检测拉获取预处理图像的边缘映射,并且选择性地采样包含图像中最丰富的结构信息所对应的一系列非重叠块;通过SVD(Singular Value Decompostion)来分解这些抽样子块,提取其稳定的鲁棒特征;借助傅里叶变换与残差机制,获取预处理图像的全局显著特征;将两种特征组合,形成中间哈希序列,再引入多维尺度机制,对其完成压缩,形成低维哈希。经过Logistic映射的加密后,得到了紧凑哈希序列;根据优化的预设阈值,基于真实图像与待认证目标之间哈希序列对应的相关系数,实现图像判别。并验证了所提方案的效率与鲁棒性。
1 紧凑哈希算法
本文基于边缘映射抽样与多维尺度压缩的紧凑哈希生成与认证过程见图1。该方案主要分为4个阶段:(1) 图像的预处理; (2) 基于边缘映射抽样与残差机制的鲁棒特征提取; (3) 基于多维尺度的哈希序列压缩; (4) 哈希序列的加密与认证。
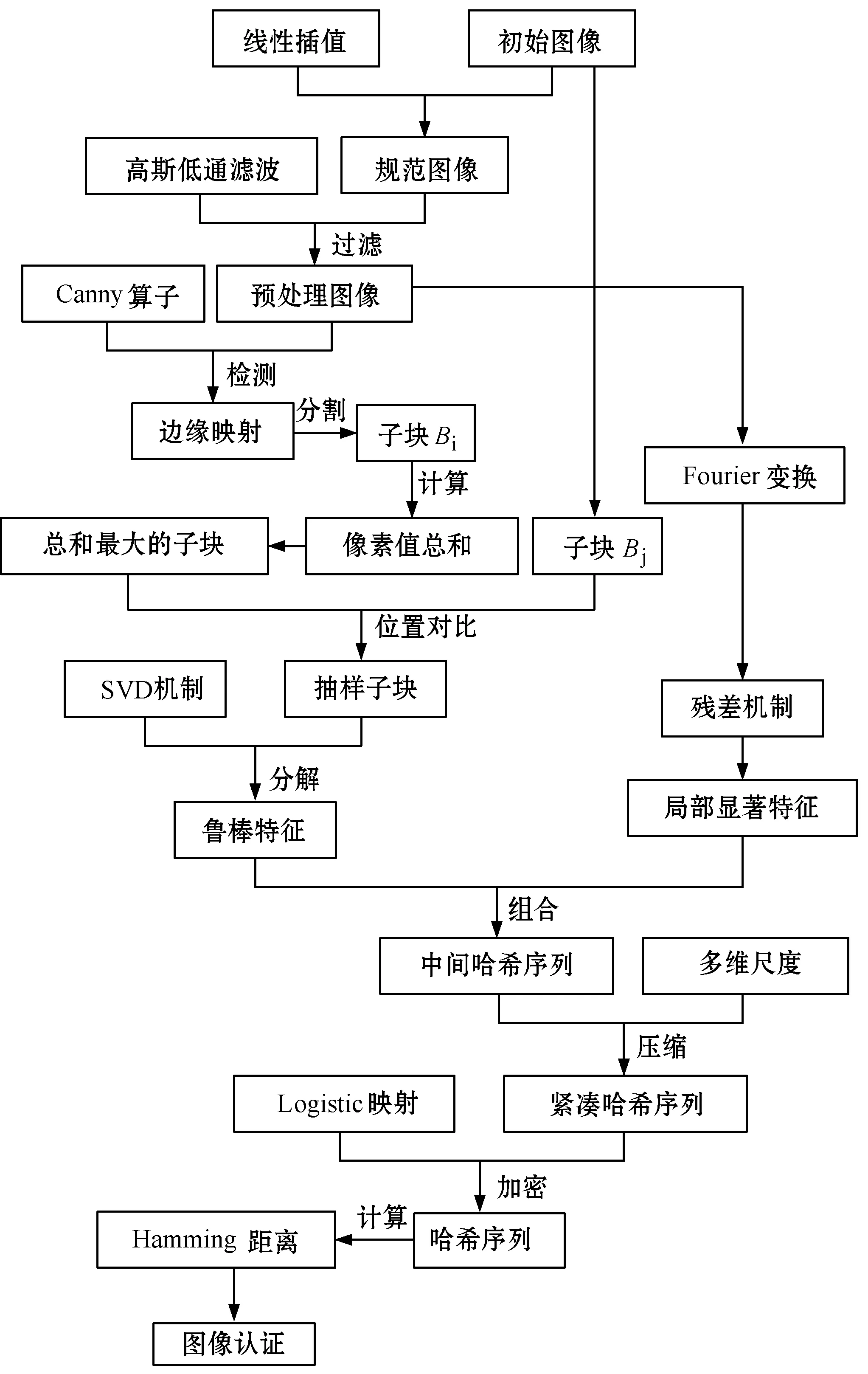
图1 本文哈希算法的生成与认证过程
1.1 初始图像的预处理
图像预处理是哈希生成的重要阶段,它能提高哈希序列对尺度缩放与噪声污染等篡改类型的鲁棒性[1]。为此,本文引入双线性插值方法[8]来处理初始图像,增强其多缩放的稳健性,使其产生的哈希序列长度不受尺寸的影响;再利用带卷积掩模的高斯低通滤波[1]来过滤插值图像,充分避免噪声污染对哈希序列的干扰。就图像中(x,y)处的高斯滤波而言,其卷积掩码为[1]:
(1)
式中:σ为卷积掩码中所有元素的标准偏差。
以图2(a)为例,其为不规则尺寸的图像,经过插值运算后,形成的规范图像见图2(b);利用高斯滤波处理后的图像见图2(c)。

(a) 不规则图像 (b) 插值图像 (c) 过滤图像图2 图像的预处理
1.2 基于边缘映射抽样与残差机制的鲁棒特征提取
完成图像的预处理后,本文利用显著性边缘映射和频谱残差机制,充分提取图像的鲁棒性,其过程见图3。令预处理图像为I,尺寸为M×M,引入双阈值Canny算子[9],来提取I的显著性边缘,有效抑制因随机噪声所引起的虚假边缘,使得形成的边缘映射有效反映I中的丰富结构信息。对于双阈值Canny算子[9],其主要有4个过程,分别是高斯滤波平滑处理、基于Soble算子的图像梯度计算、非极大值抑制、双阈值边缘检测。令两个阈值分别为T1和T2,其中,T1为高边缘灵敏度的低阈值,也就是利用T1可以检测出完整的边缘,但是容易出现虚假边缘;T2代表低边缘灵敏度的高阈值,其可以提取更准确的图像边缘,但容易去除一些实用的特征点。因此,边缘提取从低灵敏度的高阈值T2对应的计算结果开始;然后根据高边缘灵敏度的低阈值T1的计算结果,将检测的边缘像素点链接起来,得到理想的边缘映射。详细的检测过程见文献[9]。
以图2(c)为例,利用不同的T1与T2的双阈值Canny算子来提取其边缘,结果分别如图3(a)、(b)所示。依图可知,对于T1=0.05、T1=0.12的双阈值Canny算子,其提取的边缘映射中存在少量的虚假边缘。当T1=0.1、T1=0.3时,所获取边缘映射较为理想,无虚假边缘,见图3(b)。

(a) T1=0.05与T1=0.12 (b) T1=0.1与T1=0.3图3 边缘映射结果
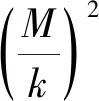
(2)

(3)
(4)


(a) 边缘映射中的子块 (b) 抽样子块图4 目标子块的抽样
随后,引入奇异值分解SVD机制[10],对抽样子块进行分解:
X=S·V·D
(5)
式中:S、D代表抽样子块的正交矩阵;V是抽样子块的对角矩阵,其含有k个奇异值。
利用式(5)处理所有的抽样子块,将其对应的奇异值组合成矢量V={v1,v2,…,vNk}。再利用傅里叶变换[11]来获取图像的显著特征。令预处理图像为f(x,y),尺寸为m×m,则其傅里叶变换为[11]:
f(x0,y0) =Fα[f(x,y)](x0,y0)

(6)
式中:Kα代表变换核;(x,y)、(x0,y0)分别是输入、输出坐标;a代表傅里叶变换的阶数。
通过式(6)处理后,输出f(x,y)对应的傅里叶频谱,即可计算其幅度B(f)=|f(x0,y0)|。接下来,借助B(f)来得到对应的log谱L(f):
L(f)=log(B(f))
(7)
利用式(7)的L(f)来计算预处理图像的平均谱E(f):
(8)
式中:*是卷积运算;gq(f)是局部滤波[12]过滤预处理图像后对应q×q维矩阵。
随后,联合L(f)、E(f),估计预处理图像的频谱残差R(f):
R(f)=L(f)-E(f)
(9)
借助逆傅里叶变换和相位频谱P(f)=arg|I(x0,y0)|,可输出对应的显著映射:
S(f)=F-1[exp(R(f))+P(f))]2
(10)
最后,引入经典的阈值分割技术[13],形成了S(f)的显著区域;并借助LBP方法[14],充分提取该区域中的局部特征S={s1,s2,…,sm}。
组合上述得到的特征矢量V={v1,v2,…,vNk}和S={s1,s2,…,sm},获取中间哈希序列h=(V,S)。为了便于后续描述,将中间哈希序列h=(V,S)记为h={h1,h2,…,hz},z=Nk+m。
1.3 基于多维尺度变换的哈希序列压缩
如果直接利用从图像中提取的特征矢量h=(V,S)视为最终的哈希序列,则其空间维度非常高,会增大算法的复杂度。因此,引入多维尺度[15],对中间哈希序列h=(V,S)实施压缩,从而形成紧凑哈希。多维尺度压缩主要分为3个过程[15]:
(1) 形成距离矩阵D。通过计算h={h1,h2,…,hz}中2个相邻元素hi、hj之间的欧式距离di,j来形成D:
(11)
(2) 计算内积矩阵B。借助步骤(1)形成的D,基于式(12),计算内积矩阵B:
(12)
其中,J代表集中矩阵;E是z×z维的单位矩阵;e代表z×1维的单位矢量。
(3) 计算低维表示G。根据式(12)可知,B为对称半正定矩阵,故可演变成:
B=SVST
(13)
其中,V代表B的对角矩阵;S代表由B的特征向量构成的矩阵。
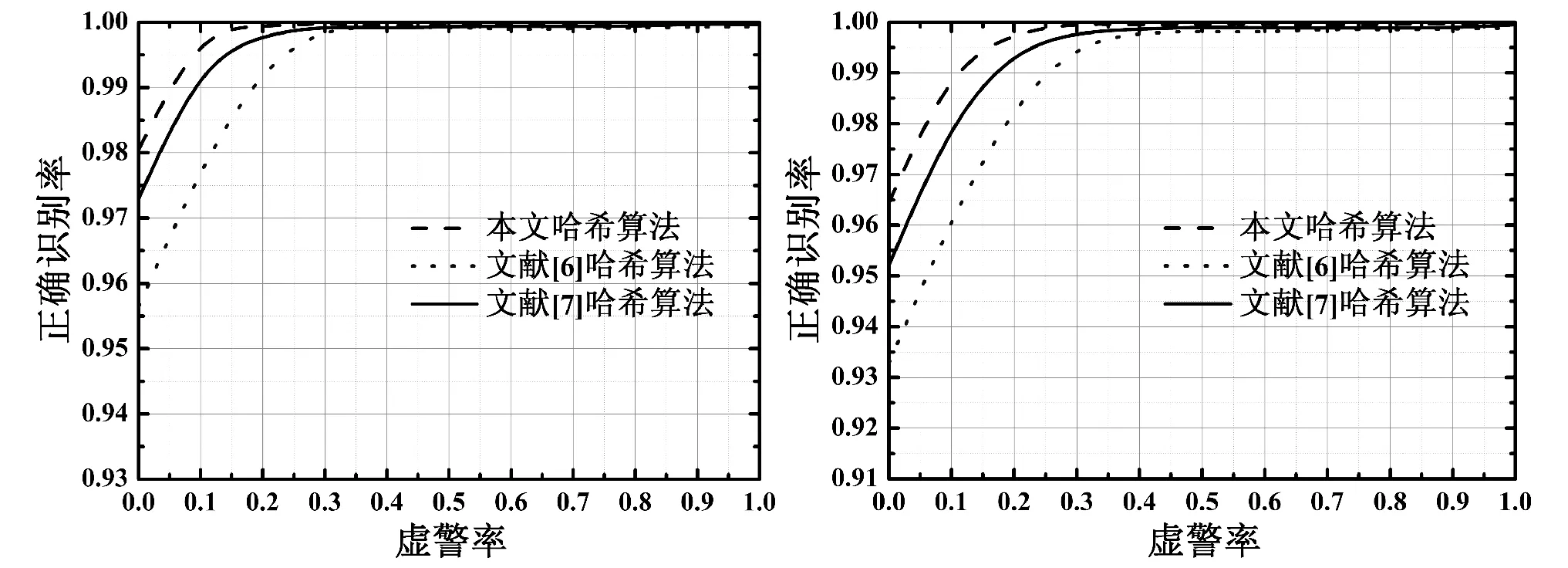
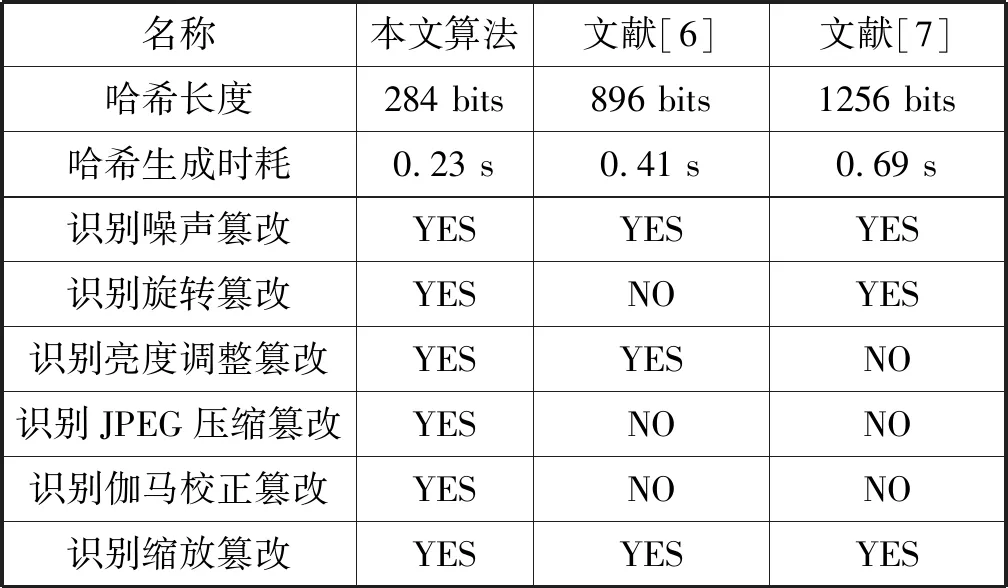
故可从矩阵Z中的前d(d (14) 为了减小G的维度,本文先计算G中每一行元素的方差;然后,根据这些方差来表示。令G={g1,g2,…,gz}T,且gi(j)是矢量gi(1≤i≤z)中的第j(1≤j≤d)个元素。则gi(1≤i≤z)的方差σ为: (15) h′(i)=Round(qi) (16) 借助式(16)量化全部的系数qi后,即可形成紧凑哈希h′={h′(1),h′(2),…,h′(r)}。 为了改善哈希算法的安全性性,引入Logistic映射[16],改变h′={h′(1),h′(2),…,h′(r)}中每个元素的值。为此,利用预处理图像的像素量来获取Logistic映射[16]的初值x0: (17) 式中:n代表预处理图像的像素数量。 再确定u值,根据式(21),可得到相应的混沌序列{x1,x2,…,xm}: xk+1=μxk(1-xk) (18) 并利用数据量化函数处理{xi}中的每个元素,形成密钥流{ki}: ki=mod(floor(xi×1014),256) (19) 随后,借助式(19)的输出结果,完成h′={h′(1),h′(2),…,h′(r)}的加密: H(i)=h′(i)⊕ki (20) 式中:H(i)是加密哈希。 (21) 式中: ⊕为异或运算;a1、a2分别是哈希H0与H1的均值;Δs是一个很小的常量,以防止式(21)的分母为零。 ρ(H0,H1)的取值范围从-1到1,其值越大,则表明二者的相似度越高[6]。随后,根据优化的阈值T,当ρ(H0,H1)≥T,则这对图像可视为相似图像;反之,则为差异图像。 通过多种实验来验证所提图像哈希方案的鲁棒性与效率。不失一般性,在UCID图像库[17]中随机选择4幅图像来测试;同时,为了反映出本文技术的优势,将文献[6]与文献[7]中的哈希方案作为对照组。根据哈希生成过程发现,主要参数值见表1。 表1 实验参数设置 在UCID库[17]中选择4幅原始图像,见图5(a)-(d),将表2的攻击类型施加给每幅图像。利用所提哈希方案拉生成这些图像之间的哈希,并统计它们之间的相关系数,结果见图5(e)-(h)。由图5可发现,对于表中的数字修改,大部分内容修改对应的相关系数值均大于0.83。为了体现这个数据的可靠性,在UCID库[17]中挑选50幅图像,基于StirMark 4.0[18]系统,将表2中的43种攻击施加于每个目标,则可形成50×43+50=2 200对相似图像。并根据式(21)统计这些相似图像对的相关系数值,数据见表3。除了旋转修改外,其最小的相关系数ρ值低于0.83;而其余操作对应的最小ρ值均高于0.83,其这些操作对应的方差都很小。因此,为了有效识别旋转攻击(见图5(f)),将阈值T适当缩小,取T=0.78时,可以准确识别上述内容修改操作,正确率为98.61%。这说明所提哈希方案具备较高的鲁棒性,在上述内容修改情况下,能够准确识别图像的真伪。 表2 不同攻击类型及其参数 (a) Madrill图像 (b) Barbara图像 (c) Lena图像 (d) Aeroplane图像 (e) 缩放修改 (f) 缩旋转修改 (g) 亮度修改 (h) 噪声修改图5 所提哈希算法的鲁棒性测试 修改类型最大值最小值均值方差尺度缩放0.998 40.889 20.970 50.019 4旋转修改0.975 30.469 50.837 90.072 7亮度调整0.996 40.836 10.963 70.020 6噪声修改10.887 90.969 20.021 3 根据整个哈希生成过程可知,其由一个安全密钥u。为了测试该方案的密钥安全性,本文利用一些列扰动因子对安全密钥u完成修改,形成了3 000组错误密钥。利用这些错误密钥来生成哈希序列,从而统计了对应的相关系数,数据见图6。根据测试数据发现,利用这3 000组错误密钥所产生的相关系数值均在零附近。因此,在非法用户不知道正确的安全密钥情况下,其很难成或估计出原始图像的相同哈希序列。这显示所提哈希方案拥有较好的安全性。原因是所提算法利用了预处理图像的像素来计算Logistic映射的初值,根据其迭代序列来完成加密,增强了哈希序列的安全性。 图6 本文哈希方案的安全性测试 为了突出所提哈希方案的优异性,统计了所提算法、文献[6]与文献[7]的ROC曲线。ROC曲线[1]是通过正确识别率PTPR和虚警率PFPR构成的,其模型如下: (22) 式中:n1代表正确决策的图像数量,n2代表误判的图像数量,M1是相似图像的总数量,M2为不同图像的总数。 图7反映了三种哈希方案的ROC曲线。根据图7可发现,所有算法对缩放、噪声这两种内容修改均具备优异的鲁棒性,呈现出良好的ROC特性曲线,三者的正确识别率均保持在0.93以上,见图7(a)、(b)。然而,对于亮度修改,文献[7]表现出更加出色的鲁棒性,所提算法与文献[6]的正确识别率均低于该方案。当PFPR=0时,文献[7]、文献[6]与所提方案的PTPR分别为926、0.817、0.883;PFPR=0.6时,三者的PTPR分别为0.998、0.991、0.994。对于旋转攻击,三者哈希方案也呈现出不同的鲁棒性,其中,所提算法对旋转修改的鲁棒性最高,当PFPR=0与PFPR=0.6时,对应的PTPR分别为0.892、0.999;此时,文献[6]的鲁棒性最低,其正确识别率低于文献[7],当PFPR=0是,文献[6]和文献[7]的PTPR分别为0.743、0.832。主要是因为所提技术、文献[6]、文献[7]的哈希生成过程都采用了插值运算与滤波的预处理措施,增强了三者对缩放与噪声的稳健性。所提哈希方案通过边缘映射抽样方法,将包含结构信息的最丰富的子块选择出来,利用稳定性较好的奇异值分解来获取其鲁棒特征,并联合傅里叶变换与残差机制,提取预处理图像的全局显著特征,将这两种特征作为哈希序列,使其对图像鲁棒特征的描述较为丰富,从而导致其对旋转修改的鲁棒性最高。但是,由于缺乏颜色空间转换,使其对亮度修改的鲁棒性较为一般。文献[7]采用了颜色空间转换方法,将图像从RGB空间映射到Lab空间后,再利用张量分解来提取亮度L分量的特征,而张量分解具有一定的稳定性,因此,该哈希技术对亮度调整具备更加理想的鲁棒性。然而,其对图像的鲁棒特征描述不充分,只提取了L分量的全局特征,使其对角度旋转的鲁棒性要低于所提技术。文献[6]则是将图像分割为非重叠子块,通过对这些子块完成列重排来获取图像的特征,对亮度与旋转修改的鲁棒性较低。 (a) 缩放变换 (b) 噪声干扰 (c) 亮度调整 (d) 旋转修改图7 三者哈希算法的鲁棒性测试 优异的哈希算法不仅具备较强的鲁棒性,而且还应具有较快的生成效率,以降低计算成本。为了客观评价这些哈希方案的哈希长度与生成效率,通过Matlab软件,在测试条件为Intel3Hz与8GB内存的微型机上实施测试,数据见表4。通过表中数据可发现,本文哈希算法由于联合多维尺度与DCT方法,有效对提取的鲁棒特征进行了压缩,充分减小了哈希维度,使其哈希长度更加紧凑,为284位,所用时间为0.23s;而文献[7]虽然只提取了图像的一种特征,并利用张量分解来获取相应的哈希序列,但是缺乏数据压缩机制,使其哈希长度最大,约为1 256位,时耗为0.69s;文献[6]则是采用了主成成分分析技术来有效压缩哈希序列,降低了哈希维度,约896位,时耗为0.41s。 表4 哈希长度和生成效率 为了获取紧凑哈希,提高其鲁棒性与安全性,本文基于边缘映射抽样与多维尺度压缩的紧凑图像哈希算法。通过对初始图像实施预处理,形成一个尺寸规范的图像;然后利用双阈值canny算子来获取其对应的边缘映射,利用其位置信息,从规范图像中抽样出包含结构信息最为丰富的子块。借助SVD机制来分解抽样子块,提取较为稳定的特征,同时,根据傅里叶变换与阈值分割、LBP算子,充分描述图像的全局显著特征。引入多为尺度机制,对这两种特征实施压缩,从而得到了紧凑哈希;通过计算真实图像与待认证图像之间哈希序列对应的相关系数,基于预设阈值,实现图像的认证。实验结果验证了所提哈希方案的合理性与优异性。 由于所提哈希方案对亮度修改的鲁棒性较为一般,后续将对颜色空间进行分析,选择对图像进行合适的颜色空间转换,利用其亮度分量来生成哈希;并考虑引入Radon变换,通过估计图像的中心信息,进一步增强所提哈希方案对任意旋转角度的鲁棒性。
1.4 哈希序列的加密与认证
2 实验结果与分析
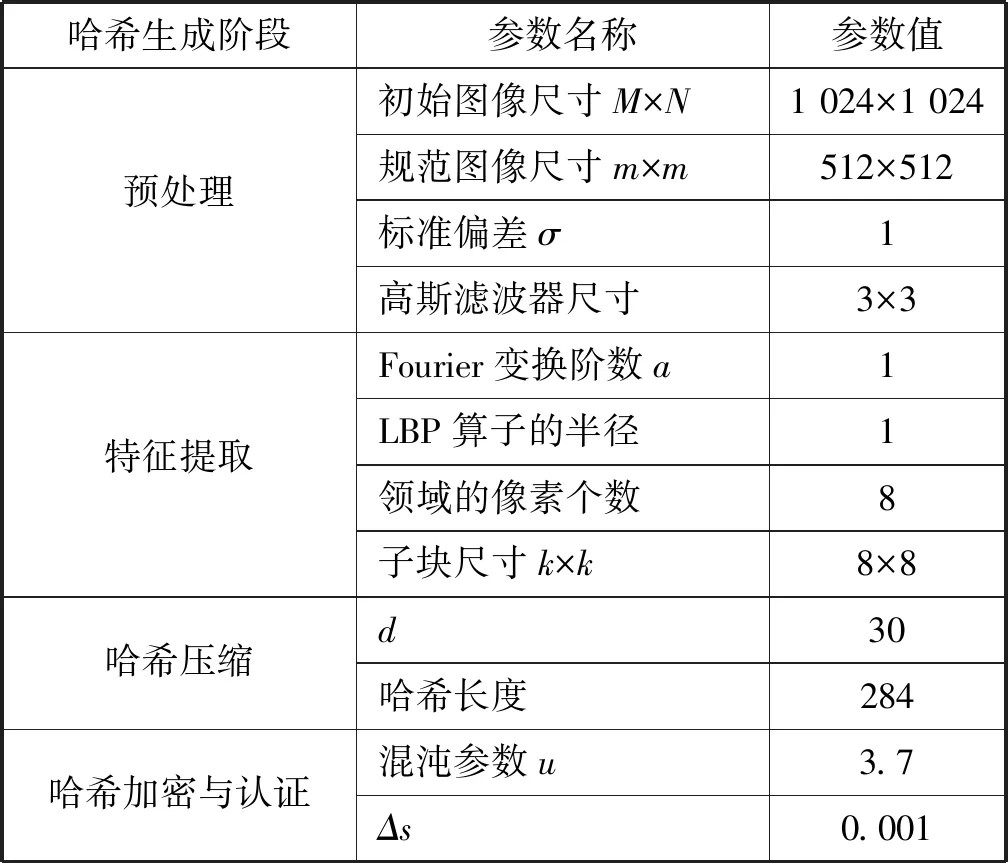
2.1 鲁棒性验证





2.2 安全性测试

2.3 不同算法的鲁棒性测试
2.4 不同算法的哈希生成效率测试
3 结 语
