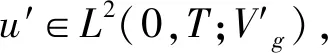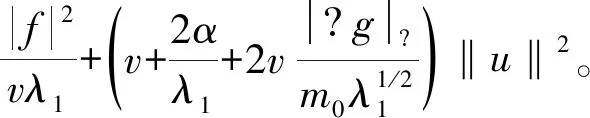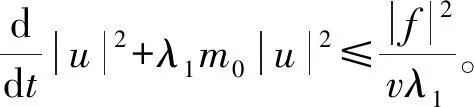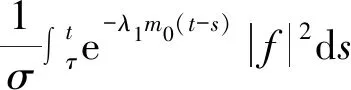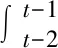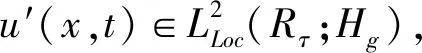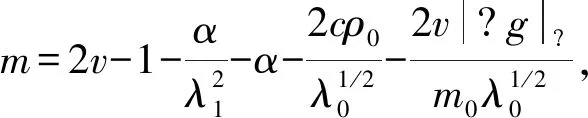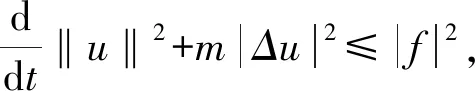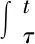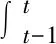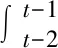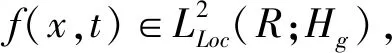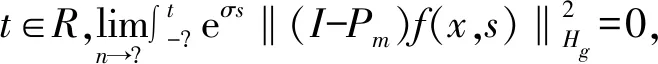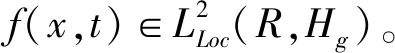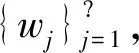有界域上含线性阻尼的二维g-Navier-Stokes方程解的拉回渐近性
2019-04-01王小霞
王小霞,高 聪,任 交,李 哲
(延安大学数学与计算机科学学院,陕西延安716000)
自从 2005年Roh J发表了《Dynamics of th g-Navier-Stokes equations》后,十多年来,有关g-Navier-Stokes方程的研究成果越来越多(文[1-6])。如Kewk M和Kwean H等研究了二维g-Navier-Stokes方程的吸引子维数;Jiang 和Hou等人研究了全空间上二维g-Navier-Stokes方程的整体吸引子存在性;Delin Wu等研究了二维g-Navier-Stokes方程指数吸引子的存在性问题。本文在此基础上,研究了含线性阻尼的二维g-Navier-Stokes方程的解的拉回渐近性问题。
含线性阻尼的二维g-Navier-Stokes方程的一般形式如下:
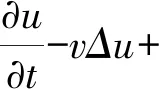
在Ω×(0,);
(1)
u(x,t)=0,在∂Ω;
u(x,0)=u0(x),在∂Ω。
这里u(x,t)∈R2和p(x,t)∈R表示速度和压力,f(x,t)是和时间有关的外力项,α代表线性阻尼,αu是与速度场平行的阻尼项,0 方程(1)等价于下面方程 (2) u(0)=0,这里Ag:Vg→Vg是g-Stokes算子。 定义1[7]设X是一个度量空间,若X中的集族{U(t,τ):X→X}(-<τ≤t<+)满足下列条件: (1)U(τ,τ)x=x,τ∈R,∀x∈X; (2)U(t,τ)=U(t,s)U(s,τ),∀τ≤s≤t,τ∈R。 则称集族{U(t,τ)}是X中的一个过程。 (1)P(∪τ<τ0U(t,τ)D(τ))在X中有界; (2)‖(I-P)(∪τ<τ0U(t,τ)D(τ))‖<ε,这里P:X→X1是一个有界投影。 定理1[7]设X是一个巴拿赫空间,U(t,τ)是X上的一个强弱连续过程,如果满足下列条件: (2)U(t,τ)满足拉回条件(C)。 另设u(x,t)∈L C(R+,Hg),(∀t>0)是方程的弱解,则 ∀t∈T,设σ=υλ1,有 证明设方程的解是u(x,t),因为 〈f-vAgu-αu-Bu-vRu,u〉= 〈f,u〉-v‖u‖2-α|u|2- 令σ=vλ1,由Gronwall引理 |u(t)|2≤|u0|2e-λ1m0(t-τ)+ |u0|2e-λ1m0(t-τ)+ |u0|2e-λ1m0(t-τ)+ 若方程的强解为: u(x,t)∈L 则∀t≥τ,可得下列结论成立: ‖u(t)‖2≤‖u(τ)‖2e-λm(t-τ)+ 证明首先用-Δu(t)乘以方程两边可得: α(u,-Δu)-(Bu,-Δu)-v(Ru,-Δu)。 根据Young′s不等式知: 2〈f,-Δu〉-2α(u,-Δu)-2(Bu,-Δu)- 2v(Ru,-Δu) ≤|f|2+|Δu|2+α|u|2+ α|Δu|2+2|(Bu,-Δu)|+ 2v|(Ru,-Δu)|≤|f|2+|Δu|2+ 2v|Ru‖Δu|。 由Poincare不等式得: |f|2。 由Gronwall′s引理可得: ‖u‖2≤‖u(τ)‖2e-λm(t-τ)+ ‖u‖2≤‖u(τ)‖2e-λm(t-τ)+ ‖u‖2≤‖u(τ)‖2e-λm(t-τ)+ 引理3[4]设Hg是Hilbert空间,其一组正交基为{Wi}i∈N。 其中Pm:Hg→span(w1,…,wn)为正交投影。 证明因为-Δ-1是Hg中的连续的紧算子,由谱算子定理,必存在一个序列{λj}j=1,0≤λ1≤λ2≤…≤λi≤…≤λj→0,当j→。 设Vm=span{w1,w2,…,wn}⊂Vg, 正交投影Pm:Vg-Vm, ∀u∈D(-Δ),令 u=Pmu+(1-Pm)u=u1+u2。 在Hg中取-Δu2,与方程(2)两边做内积 (B(u),-Δu2)+v(Ru,-Δu2)=(f,-Δu2)。 利用Young′s不等式 |B(u),-Δu2|≤|(B(u1,u1+u2),-Δu2)| +|(B(u2,u1+u2),-Δu2)|≤ 其中 |(Ru-Δu2)| ≤|Ru|·|Δu2|≤ 2(B(u),-Δu2)-2v(Ru,-Δu2)- 利用Gronwall引理,可得: ‖u2‖2≤‖u2(t0+1)‖2e-vλm+1α(t-(t0+1)) ‖u2(t0+1)‖2e-vλm+1α(t-(t0+1))+ ‖u2(t0+1)‖2e-vλm+1α(t-(t0+1))+ 由引理3,∀ε>0,当取m+1充分大时, ‖u2(t0+1)‖2e-vλm+1α(t-(t0+1))≤ 故有‖u2(t)‖2≤ε,∀t≥t2。 则Vg中的过程族{U(t,τ)}满足拉回条件(C),故定理2成立。1 相关定义
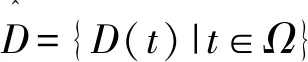
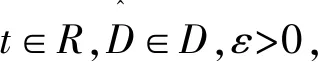
2 主要结果