关于Smarandache可乘函数的β次混合均值

杨张媛，赵西卿

(延安大学数学与计算机科学学院，陕西延安716000)

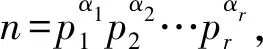
本文利用初等方法证明了如下定理：

定理对任意实数x≥3，当β>1时，有渐近公式

其中ζ(n)为Riemann zeta-函数。

1 相关引理

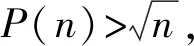
SM(n)=P(n)；

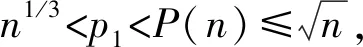
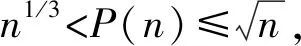
SM(n)=2P(n)。

引理2 对任意实数x≥3，有

(1)当β>2时，有估计式

(2)当1<β≤2时，有估计式

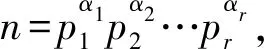
SM(n)>P(n)，当β>2时，有

x(β+2)/3lnβ-1x。

当1<β≤2时，由上式以及s>0，s≠1，

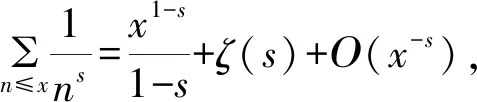
x(β+2)/3lnβx。

综上，此引理得证。

引理3 对任意素数p和正实数α，当实数x≥3时，有

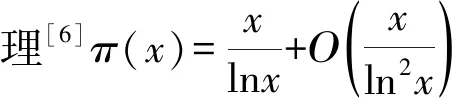
与Abel恒等式[7]可得

综上，引理得证。

2 定理的证明

证明记P(n)=p，结合引理1可得

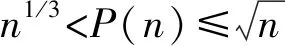
A={n|n=mP(n),P(m)≤n1/3}，

根据引理1可得

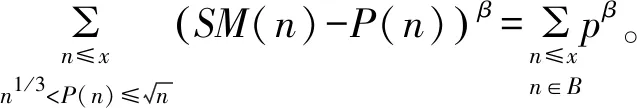
又由于当β>1时，有

综上所述，有结论

定理得证。