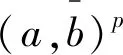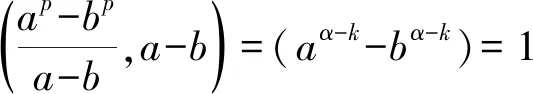关于Smarandache LCM函数的两类下界估计

郭梦媛，高 丽，郑 璐

(延安大学 数学与计算机科学学院陕西延安716000)

对于任意正整数n，著名的F.Smarandache LCM函数定义为最小的正整数k，使得n|[1,2,…k]，即SL(n)=min{k:k∈N+,n|[1,2,3…k]}。从SL(n)的定义容易推出，如果用n=p1α1p2α2p3α3…prαr表示n的标准分解式，那么SL(n)=max{p1α1·p2α2·p3α3·…prαr}。因此当n较小时，不难算出SL(1)=1，SL(2)=2，SL(3)=3，SL(4)=4，SL(5)=5，SL(6)=3，SL(7)=7……近年来关于SL(n)的各种性质许多学者都进行了研究，尤其在下界估计这方面获得了不少有意义的结果，例如：

文献[1]中作者针对函数S(2p-1(2p-1))的下界估计问题做了研究，给出了结论：S(2P-1(2P-1))≥2p+1,p为任意素数。

而文献[2]在上述结论的基础上针对函数S(2P-1(2P-1))的下界估计问题进行了更深入的讨论，得到了更强的估计式：S(2P-1(2P-1))≥6p+1，其中p≥17为任意素数。

文献[3]对SL(2p+1)的下界估计问题做了研究，得到SL(2p+1)≥6p+1，其中p≥17为任意素数。

文献[4]对S(n)在特殊数列ap+bp上的下界估计问题进行了研究，证明了当a与b为任意不同的正整数时有估计式：S(ap+bp)≥10p+1，其中p≥17为任意素数。

文献[5]对Z(n)在特殊数列ap+bp上的下界估计问题进行了研究，证明了当a与b为任意不同的正整数时有估计式：Z(ap+bp)≥10p，其中p≥17为任意素数。

文献[6]对S(n)在特殊数列ap-bp上的下界估计问题进行了研究，证明了当a与b为任意不同的正整数时有估计式：S(ap-bp)≥8p+1，其中p≥17为任意素数。

史婵[7]对函数S(2p+1)的下界估计问题做了研究，得到S(2p+1)≥6p+1，其中p≥17为任意素数。

本文在上述结论的基础上对Smarandache LCM函数在数列ap+bp和ap-bp上的下界估计问题进行了研究，通过初等方法和组合方法得到了一个较强的估计式，结果如下：

定理1 设p≥17为任意素数，对于任意互素的正整数a与b，有估计式

SL(ap+bp)≥10p+1。

定理2 设p≥17为任意素数，对于任意互素的正整数a与b，有估计式

SL(ap-bp)≥10p+1。

1 相关引理

引理1[8]：设p为奇素数，对于任意互素的正整数a与b，且a+b≠0都有

引理2[9]：对于任意素数p，正整数n，以及α，都有

(1)p|n时，有SL(n)≥p,且p|SL(Pα)；

(2)有SL(Pα)=Pα；

(3)如果n是一个素数，则有SL(n)=S(n)。

引理3[10]：设a与b为正整数，且a+b为奇数，则对任意素数p≥3，有不等式

2 定理的证明

这部分我们将利用初等方法和组合方法给出定理1和2的证明，证明过程如下：

定理1的证明：

因为a和b为不同的整数，设(a,b)=d。则存在a1以及b1，使得a=d×a1,b=d×b1，且(a1,b1)=d。从而有

ap+bp=dp(a1p+b1p)。

(1)

再由Smarandache LCM函数的性质可知：

SL(ap+bp) ≥SL[dp(a1p+b1p)]≥

SL(a1p+b1p)。

不失一般性，由(1)式可知，我们可以假定定理1中的a,b满足(a,b)=1，且a·b>1。对于任意素数q|n。有SL(n)≥p,且q|SL(Pα)对所有正整数成立。

首先，我们证明ap+bp不可能为p的方幂，若不然，设ap+bp=pα，当α=2时，有ap+bp≥2p+1≥2p≥p2，所以α≥3。由引理1不难推出a+b=pαv，≤1k≤α-2且(v,p)=1，再由

pα=ap+bp=ap+(vpk-a)p=

或者

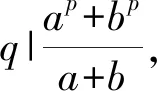
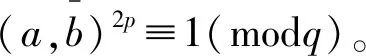
(2)

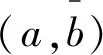
ap+bp=ap+(a+hq)p=

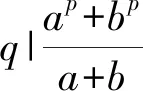
q=h·2p+1。

(3)

于是由(3)式可知：

当ap+bp除p之外，至少含有4个不同的素因子时，一定有一个素因子q使得q=h·2p+1且h≥5，因为当素数p≥5时，两个素数2p+1和4p+1中至少有一个被3整除，因此2p+1和4p+1不可能同时为素数。此时

SL(ap+bp)≥SL(q)≥S(q)=q=

h·2p+1≥10p+1。

下面讨论当ap+bp含有三个不等于p的素因子q1,q2,q3的情况。

由(3)式可以设q1=h1·2p+1，q2=h2·2p+1，q3=h3·2p+1，且有h1

接下来讨论当ap+bp含有两个不等于p的素因子q的情况。

由(3)式ap+bp中不可能同时包含有素因子2p+1和4p+1，也不可能同时包含素因子4p+1和8p+1，因此由⑶式以及SL(n)的性质，最多有三种形式

ap+bp=pα(2p+1)β(8p+1)γ；

ap+bp=pα(2p+1)β(6p+1)γ；

ap+bp=pα(4p+1)β(6p+1)γ。

若ap+bp=pα(2p+1)β(8p+1)γ成立，则当β≥5或γ≥2时，由引理2知

SL(ap+bp)≥SL[(2p+1)β]=(2p+1)5≥

5(2p+1)≥10p+1，

或者

SL(ap+bp)≥SL[(8p+1)γ]=(8p+1)2≥

2(8p+1)≥10p+1。

于是可以设1≤β≤4，γ=1。现在证明，当p≥5时，ap+bp不可能含有p的方幂，否则当α≥2时，由Euler-Fermet定理知：ap≡a(modp)，bp≡b(modp)即a+b≡ap+bp≡0(modp)。设a+b=pαv，(v,p)=1。由引理1可知k=α或k=α-1，显然ap+bp=pα(2p+1)β(8p+1)，且1≤β≤4，k=α这不可能成立，因为此时有

则显然有(pα·v+1)p+(pα·v-1)p≥

2ppα(2p+1)β(8p+1)，相矛盾。

因此，可以设k=α-1。从而有a+b=pα-1v，由引理3可知

pα(2p+1)β(8p+1)。

pα(2p+1)β(8p+1),相矛盾。

当α=1时，因为有a+b≡0(modp)，所以有

a+b=pv，又因为

pα(2p+1)β(8p+1)=ap+bp≥

通过计算可知(p·v+1)p+(p·v-1)p>

pα(2p+1)β(8p+1)，相矛盾。

所以ap+bp不可能含有素因子p，则有ap+bp=pα(2p+1)β(8p+1)，且有1≤β≤4首先需证ap+bp=pα(2p+1)β(8p+1)。

由a+b≡ap+bp≡(2p+1)4(8p+1)≡

1(modp)，设a+b=mp+1。由引理1可得

这就可以推出m=8，即a+b=8p+1，由于

ap+bp=(2p+1)4(8p+1)。

因为有(4p+1)p+(4p)p>(2p+1)4(8p+1)，相矛盾，即ap+bp>(2p+1)4(8p+1)，而当1≤β≤4时，显然(2p+1)4(8p+1)>(2p+1)β(8p+1)=ap+bp矛盾。

同理也可证当p≥17时

ap+bp=pα(2p+1)β(6p+1)γ与

ap+bp=pα(4p+1)β(6p+1)γ这两种情况下，定理1也成立。

最后来讨论当ap+bp只含有一个不等于p的素因子q的情况。

这时候只需要讨论以下四种情况：

ap+bp=pα(2p+1)β；

ap+bp=pα(4p+1)β；

ap+bp=pα(6p+1)β；

ap+bp=pα(8p+1)β。

若ap+bp=pα(2p+1)β成立。则当β≥5时，有估计式

SL(ap+bp)≥SL[(2p+1)5]=(2p+1)5≥

5(2p+1)≥10p+1。

当β≤4时，由前面的证明过程可知当p≥5时，如果α≥1则ap+bp=pα(2p+1)β就不可能成立，同样当α=0时，ap+bp=pα(2p+1)β，且有1≤β≤4，也不成立。

同理可以证明其余三种情况

ap+bp=pα(4p+1)β；

ap+bp=pα(6p+1)β；

ap+bp=pα(8p+1)β。

综上所述，定理1得证。

定理2的证明：

由引理2中伪Smarandache LCM函数SL(n)的性质知：对于任意的素数p，若p|n时，有SL(n)≥SL(p)≥p，而且p|SL(pα)，对任意满足α≥p的正整数α都成立。所以对任意素数p≥17，令q为ap-bp的任意素因子，显然q≥3，易得SL(ap-bp)≥q，又因为q|(ap-bp)，因而ap-bp≡0(modq)或者

(4)

q=2kp+1,k∈N+。

(5)

首先证明ap-bp为p的方幂。

假设ap-bp=pα。当α=2时，有ap-bp≥2p-1≥p2，所以α≥3。由引理1可推出a-b=pα·v，其中k∈N+，(p,v)=1，因为a-b|ap-bp，从而v=1。

SL(ap-bp)≥ap-bp≥q≥2·5p+1≥10p+1。

接下来讨论除p以外，ap-bp至少含有4个素因子。

由(4)式可知，至少存在一个素因子q，使得q=2kp+1，其中k≥5。因此当素数p≥5时，2p+1和4p+1不可能同时为素数。因此：

SL(ap-bp) ≥SL(q)=q=

2·kp+1≥10p+1。

然后来讨论除p以外，ap-bp只含有3个素因子q1,q2,q3。

由(4)式可知，q1=2k1p+1，q2=2k2p+1，q3=2k3p+1，而当p≥17时，2p+1和4p+1不可能同时为素数，则至少存在一个素因子。不妨设为q1，此时q1=2k1p+1≥8p+1，k1≥5。则一定有

SL(ap-bp)≥q1≥2·k1p+1≥10p+1。

再讨论除p以外，ap-bp只含有2个素因子。

由(4)式可知，ap-bp不可能同时包含素因子2p+1和4p+1。因此由(2)式及SL(n)的性质，可以分为以下形式：

ap-bp=pα(2p+1)β(6p+1)γ；

ap-bp=pα(2p+1)β(8p+1)γ；

ap-bp=pα(4p+1)β(6p+1)γ。

若ap-bp=pα(2p+1)β(6p+1)γ成立，当p≥5，或γ≥2时，由引理2知

SL(ap-bp)≥SL[(2p+1)β]≥(2p+1)β≥

4(2p+1)≥10p+1，

或者SL(ap-bp)≥SL[(6p+1)γ]≥

(6p+1)γ≥2(6p+1)≥10p+1。

当1≤β≤5且γ=1时，在这种情况下，当p≥17时ap-bp不可能含有p的方幂。否则，当α≥2时，根据Eluer-Fermat定理可知：ap≡a(modp)，bp≡b(modp)，即a-b≡ap-bp≡0(modp)。再由p|(a-b)，可设a-b=pαv，(v,p)=1。由引理1可知k=α或k=α-1，显然ap-bp=pα(2p+1)β·(6p+1)γ且1≤β≤5，k=α是不可能的。因为此时

pα(2p+1)β(6p+1)γ=(ap-bp)≥

相矛盾，同理可以推出当k=α-1，也是矛盾的。

如果α=1时，由于a-b≡ap-bp≡0(modp)。可以得到k=α=1，有pα|(ap-bp)，显然这是不可能的，因此ap-bp此时不含素因子p，于是有

ap-bp=pα(2p+1)4(6p+1)，其中1≤β≤5，且p≥17为任意素数。通过计算可以得到上式不成立。

同理可证，当ap-bp=pα(2p+1)β(8p+1)γ与ap-bp=pα(4p+1)β(6p+1)γ，素数p≥17时，结论SL(ap-bp)≥10p+1成立。

最后讨论除p以外，ap-bp只含有1个素因子。

因而由(4)式及SL(n)的性质，可以考虑以下四种形式：

ap-bp=pα(2p+1)β；

ap-bp=pα(4p+1)β；

ap-bp=pα(6p+1)β；

ap-bp=pα(8p+1)β。

若ap-bp=pα(2p+1)β成立，当β≥5时，由引理2有：

SL(ap-bp)≥SL[(2p+1)β]=(2p+1)β≥

5(2p+1)≥10p+1。

当β≤4时。由前面的证明过程可知ap-bp不含有除p以外的素因子。因此当α≥1则ap-bp=pα(2p+1)β，且有1≤β<4，就不可能成立。因此

ap-bp=pα(2p+1)β，

当β=4，ap-bp=pα(2p+1)β有

a-b≡ap-bp≡(2p+1)4≡1(modp)。

而a-b|ap-bp所以可设a-b=(2p+1)n，由引理(1)可知

((2p+1)4-n,(2p+1)n)=1。

所以n=0或n=4，即a-b=1或a-b=(2p+1)4，这与(a,b)=1，且a≥b+1，p≥17以及a-b

同理可证，当ap-bp=pα(4p+1)β，

ap-bp=pα(6p+1)β和ap-bp=pα(8p+1)β时结论也成立。

于是定理2得证。