基于PSO-WNN模型的超短期风速预测及其误差校正
2019-03-31丁方莉周松林杨洪深
丁方莉,周松林,杨洪深
(铜陵学院电气工程学院,安徽铜陵244061)
风速及风电功率的随机性和不可控性会导致风电机组并网后对电网产生较大的干扰[1-3]。近年来,随着风电并网规模的日益增加,对风速进行准确预测显得尤为重要。风速及风电功率预测方法分为物理方法与统计预测方法。其中统计预测法不要求提供具体的地理信息,仅根据历史气象数据即可开展预测,因而应用较为广泛。统计预测模型包括时间序列法[4]、神经网络法[5-6]、卡尔曼滤波法[7]、支持向量机[8-9]等。针对风速时间序列的非平稳特性,一些学者采用分解-合成的预测方法取得了良好的效果,如文献[10]将经验模式分解和神经网络相结合进行短期风速组合预测;文献[11]将风速进行小波分解,采用支持向量机对各层小波系数进行预测,通过小波重构得到最终风速预测值。小波神经网络(wavelet neural network,WNN)是小波函数与神经网络相结合而构成的新型神经网络,同时具有神经网络自学习功能和小波函数多分辨率局部时频特性,但小波神经网络的参数较多,且参数的选择对预测性能的影响很大。传统小波神经网络通过最优梯度下降法调整网络权值和小波函数的尺度因子、平移因子,但往往陷入局部最优解。粒子群优化算法(particle swarm optimization,PSO)是一种智能最优化算法[12],将其应用于小波神经网络的参数优化能够增加获取全局最优解的概率,改善神经网络对高维函数的逼近性能,提高预测精度。为此,文中提出一种基于PSO-WNN模型的超短期风速预测方法,同时分析预测模型的误差构成及其影响因素,采用一阶线性回归法对模型误差进行校正,以期提高风速预测模型的泛化性能和预测精度。
1 PSO-WNN模型
1.1 小波神经网络
将小波函数作为神经网络的激励函数即构成小波神经网络。小波函数可表示为

式中:ψ(·)为母小波;a 为伸缩因子或尺度因子,a >0;b 为平移因子。文中风速预测模型采用图1所示的三层小波神经网络结构。
设X=[x1,…,xd]为d 维输入向量,其元素为风速、风向、温度等;y 为一维输出向量,即待预测风速;vij,wj为连接权;N 为隐节点数。隐层神经元的激励函数选小波函数ψ(x),通常取Morlet小波,如
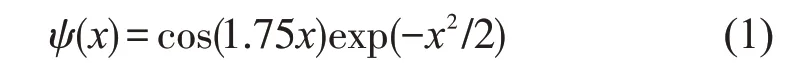
设共有M 个输入输出样本对X=[X1,…,XM] ,Y=[Y1,…,YM],其中第m 个d 维样本及其对应输出为Xm=[x1m,…,xdm],Ym=ym。Zj=[zj1,…,zjm]为第j个隐层单元输出,则对于第m 个输入样本,网络的第j 个隐单元输出为

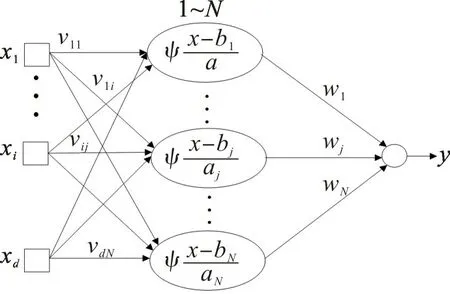
图1 小波神经网络结构Fig.1 Construction of wavelet neural network

其中i=1,…,d。网络输出为wj0为第i 个节点阈值。假设网络输入样本Xm对应的期望输出为dm,通过训练样本对网络进行训练,实现目标函数(5)式最小化,从而确定参数a,b,v,w。

1.2 PSO-WNN参数优化算法
1.2.1 基本粒子群算法
基本粒子群算法,即首先将需求解的问题转化为一群不同长度且具有个体适应度的粒子,然后粒子们追随当前最优粒子在解空间中搜索,通过迭代方法搜寻使目标函数最小化的最优解。对于WNN模型,粒子应该包含连接权vij与wj、伸缩因子aj、平移因子bj等参数对应的二进制串码。设d 维空间中第i 个粒子的位置、速 度、个 体 最 优 解 分 别 为 Xim=(xi,1,xi,2,…, xi,d),Vi=(vi,1,vi,2,…, vi,d),Pi=(pi,1,pi,2,…, pi,d),在 群 体X=(x1,x2,…, xd)中全局最优解Pg=(pg,1,pg,2,…, pg,d)。每次迭代时,粒子通过跟踪个体最优解和全局最优解更新自己。在寻找这两个最优解时,粒子的位置和速度更新公式如下:
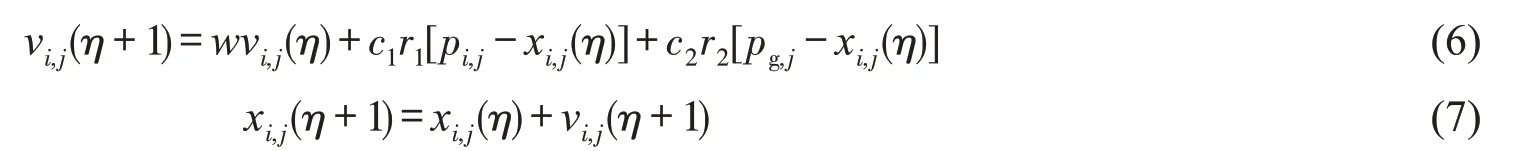
式中:η 为进化代数;vi,j,xi,j,pi,j和pg,j分别为粒子i 在d 维空间上的速度、位置、个体极值和全局极值;c1,c2为正的学习因子,通常取2;r1,r2为0到1之间均匀分布的随机数;w 为惯性权。
1.2.2 二阶振荡粒子群算法
在基本粒子群算法中,粒子的飞行速度仅是当前位置的函数。为平衡PSO全局搜索能力和局部改良能力,文中在速度更新过程中,引入粒子位置的变化量以提高群体的多样性和全局收敛性,同时引入振荡环节,构成二阶振荡粒子群算法,其速度更新公式为
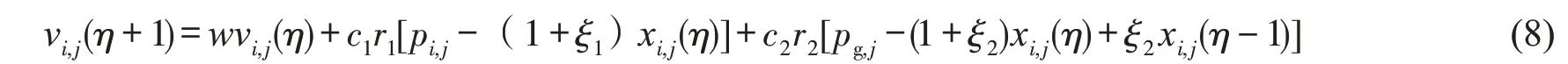
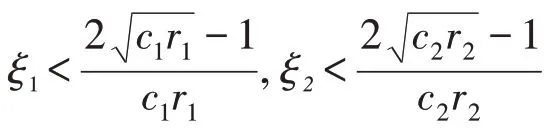
文中采用预测值均方根误差的倒数作为适应度函数,即

其中:H为样本个数;vR为实测值;vP为预测值。
1.2.3 PSO-WNN参数优化步骤
1)按照连接权值和小波参数的数量确定粒子的个数和每个粒子的二进制位数,并随机初始化种群中各粒子的速度和位置。
2)将每个粒子转化为待优化参数a、b、v、w,应用该参数对训练样本进行预测,按式(9)计算各粒子适应度函数值及位置。
4)将每个粒子每次迭代得到的适应度函数值与过去的最好位置作比较,如果适应度函数值更大,说明误差减小,则将其作为新的当前最好位置。
5)每次迭代均比较当前所有个体最优解从而得到全局最优解。
6)当迭代达到最大次数或预设精度时则搜索停止,输出结果,否则返回步骤3)。
2 超短期风速预测及误差分析
2.1 超短期风速预测
k近邻算法能够在众多历史数据形成的向量中寻找与当前向量模式最近的k个向量,对模型进行训练和预测,通过k近邻算法对样本进行筛选,能够防止一些突变量和奇异量对模型的干扰,提高模型的范化性能和预测精度。基于k近邻算法的PSO-WNN风速预测步骤如下:
1)预测模型不同的输入变量可能具有不同的量纲,不利于网络训练,需做归一化处理,即将原始数据通过线性变换至[0,1]区间,再通过相空间重构构造d维输入样本向量集合
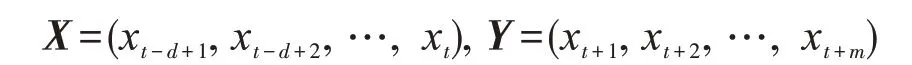
其中:X 为WNN 的d 维输入向量;Y 为m 维输出向量,即超前m 步预测,对于单步滚动预测模式,m=1。
2)采用k近邻算法,以欧式距离为评价依据,从样本集向量X中选出与当前预测时段对应的向量欧式距离较小的k组输入向量作为训练集。
3)根据样本集建立如式(5)所示的目标函数,运用二阶振荡粒子群优化算法对WNN网络进行训练并确定WNN参数。训练好的WNN能够描述满足目标函数的高维函数F,即Y=F(X)。
4)以单步预测为例,将当前观测值向量代入WNN模型即可得到预测值,并进行误差分析。对于多步预测,可以采取单步滚动预测方式,即将上一次预测值当作观测值更新到历史样本中,再进行下一步预测。滚动预测通常会带来误差累积,所以超前步长越多,误差越大。
为衡量预测精度,文中定义两种误差,平均绝对误差(EMAE)和均方根误差(ERMSE)。

2.2 误差分析
对于时段t,均方误差Err(t)可以表示为
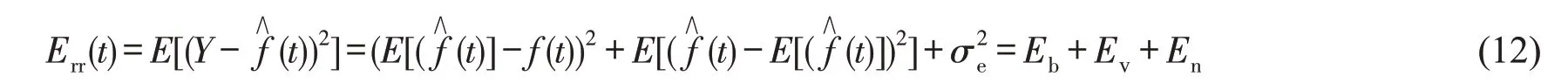
式(12)表示的预测误差来自三个方面:因简单模型无法表示基本数据的复杂度而造成的偏差Eb;因复杂模型对训练其所用的有限数据过度敏感而造成的方差Ev;不可消除的噪声项误差En。其中偏差与方差取决于模型复杂度与训练样本集的容量,合称为模型误差。偏差源于模型对样本的欠拟合,如果模型具有足够的数据,但因不够复杂而无法捕捉基本关系,则会出现偏差。方差通常出现在模型过于复杂或没有足够的样本支持的情况下,方差过高则表示模型对训练集高度敏感即过拟合,模型泛化能力差,增加样本是降低模型方差的有效途径。噪声项误差是由外界随机干扰带来的,通常表现为零均值正态分布。
图2 为模型误差与模型复杂度的关系。由图2可见,在给定一组固定数据时,模型不能过于简单或复杂。模型过于简单,则偏差较大、方差较小;模型过于复杂,则方差较大、偏差较小,两种情况的总体误差不能达到最小。因此减小总体误差的关键在于解决模型复杂度与样本容量的矛盾。实际应用中没有一个明确的解析方法来解决这一矛盾,往往是通过多次比较实验来折中考虑,这样的模型只能是相对最优的。模型误差与模型复杂度、样本容量、训练程度以及参数初始化等因素有关,通常使总体误差呈现均值不为零的近似正态分布。文中算例采用一阶线性回归法对模型误差进行校正,校正后的总体误差将会适度减小且呈正态分布。
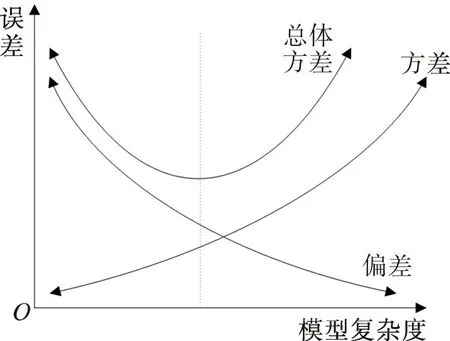
图2 模型误差与模型复杂度的关系Fig.2 Relationship between model error and model complexity
3 算例仿真分析及模型误差校正
3.1 算例分析
文中采用MATLAB2012进行仿真实验,所用风速数据取自澳大利亚某风电场2014年6—8月份的风速数据。PSO-WNN算法的时效性和精确度存在一定矛盾,适当减小目标函数值和训练样本容量可减少时间消耗,但会牺牲一定的预测精度。因此首先剔除非正常数据,再从中截取1 600个数据用于仿真分析。样本分为训练样本集、测试样本集、验证样本集等3个子集。其中:训练样本集容量为700,用于训练预测模型;测试集样本集容量为800,用于获取误差样本,构建一阶线性拟合函数;验证集样本容量为100,用于验证预测性能。先将风速样本数据归一化到[0 1]区间,再进行相空间重构,将时间序列转化为矩阵形式[X Y],其中X=(xt-d+1,xt-d+2,…,xt),Y=(xt+1,xt+1,…,xt+m),d 为输入向量的维数。预测模型的结构与参数目前还没有一个准确的确定方法,在实践中通常是通过多次实验比较来确定。该算例预测模型的参数设定:输入向量的维数d=6,WNN 模型隐层节点数N=8,PSO 目标函数归一化取值为0.01,种群数量为80。表1 为PSO-WNN,WNN,BP 3种模型的训练与预测结果。

表1 3种模型训练及预测结果Tab.1 Training and prediction results of three models
从表1 可以看出:PSO-WNN预测值的平均绝对误差MAE为2.17 m/s,均方根误差RMSE为2.54 m/s;相比单一的WNN和BP预测模型,POS-WNN模型的预测准确度有所提高,但模型的时效性不高,训练时间达332.3 s。模型的时效性与训练样本容量、WNN网络结构复杂性、PSO目标函数值、种群数量等因素有关。经反复实验,当训练样本容量取400,WNN模型隐层节点数取6,PSO目标函数归一化取值为0.02,种群数量为55 种时,PSO-WNN模型的时间消耗减少至203.3 s,但预测误差RMSE增大至3.01。可见模型的时效性和准确度存在一定的矛盾,需综合考虑,折中取值。
为进一步验证PSO-WNN模型的实用性和稳健型,将PSO-WNN,WNN模型用于两个不同风速级别和时间采样间隔的风电场风速预测,结果如图3,4。图3 为小时级采样风速的预期曲线,平均风速为9.2 m/s。图4为采样间隔为15 min的风速预测曲线,平均风速为1.3 m/s。比较图3,4可看出,在不同级别和不同采样间隔的场景下,与WNN模型相比,PSO-WNN模型获得了更高的预测精度,表现出更强的稳健性。
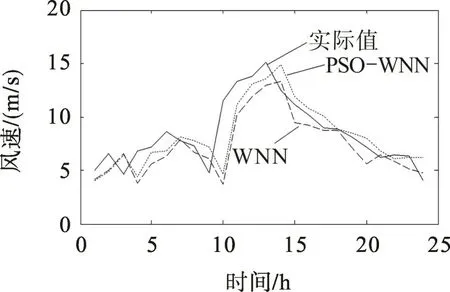
图3 小时级风速预测曲线Fig.3 Prediction curves of hourly wind speed
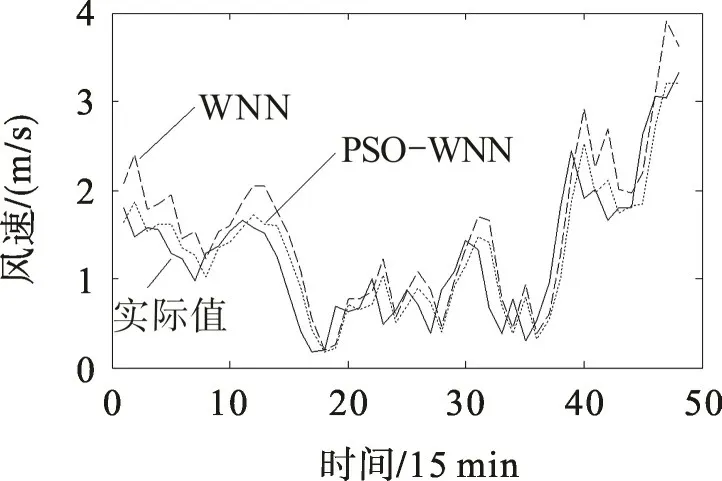
图4 15 min级风速预测曲线Fig.4 Prediction curves of 15 min level wind speed
3.2 模型误差校正
图5为800个测试样本的实际风速和预测风速散点图,根据散点图采用一阶线性回归法求取实际风速与预测风速之间的拟合函数。设拟合函数为

式中k,b 为拟合函数的系数。对样本点进行拟合得到一阶线性回归方程为
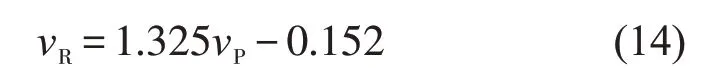
由图5可以看出,散点图位置整体偏上,拟合直线角度大于45°,样本点较分散地对称分布于拟合直线两侧。说明预测值总体小于实际值,存在均值为负的模型误差。将测试样本的预测值按式(14)进行校正得到校正后的预测值,如
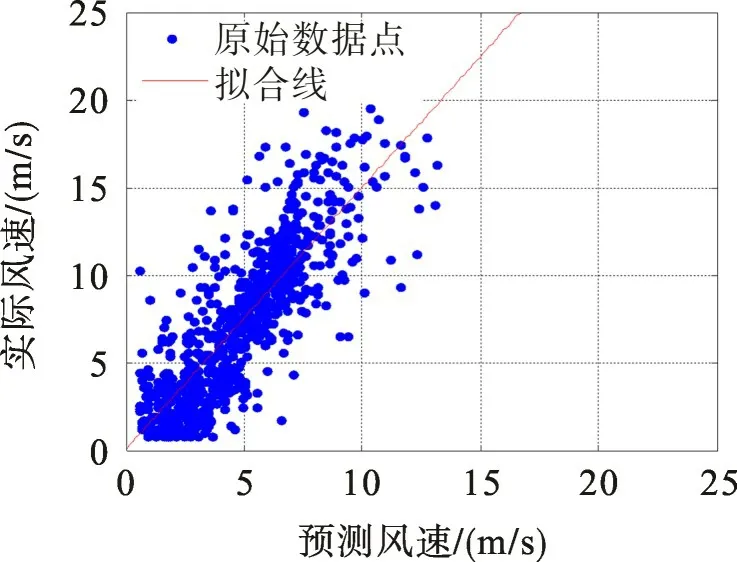
图5 校正前散点图Fig.5 Scatter before correction

重新作出校正后测试集的预测风速和实际风速的散点图,如图6所示。对图4散点图再次进行一阶线性回旭,得到新的拟合方程为

对比图5,6可以发现,校正后系统误差减小,风速样本对称分布在近似为45°的拟合直线两侧,且散点更向拟合直线靠拢,预测误差减小。图7为测试集样本校正前后预测误差的概率密度曲线。由图7可看出:校正前的误差概率密度曲线向左倾斜,百分比误差分布在[-0.60,0.25]区间,均值小于零;校正后的误差概率密度曲线更为集中地对称分布在[-0.25,0.25]区间,误差均值接近于零,说明校正后的模型误差得到一定程度的降低,且呈正态分布。当测试集样本容量足够多时,式(11)能够表征该模型预测风速和实际风速的线型关系,可用于后续验证集样本的误差校正。图8,9是式(11)对100个验证集样本校正前后的预测曲线。由图8,9可见,校正后的预测误差得到了一定程度的减小,说明采用一阶线性回归法能够在一定程度上实现预测误差的校正。
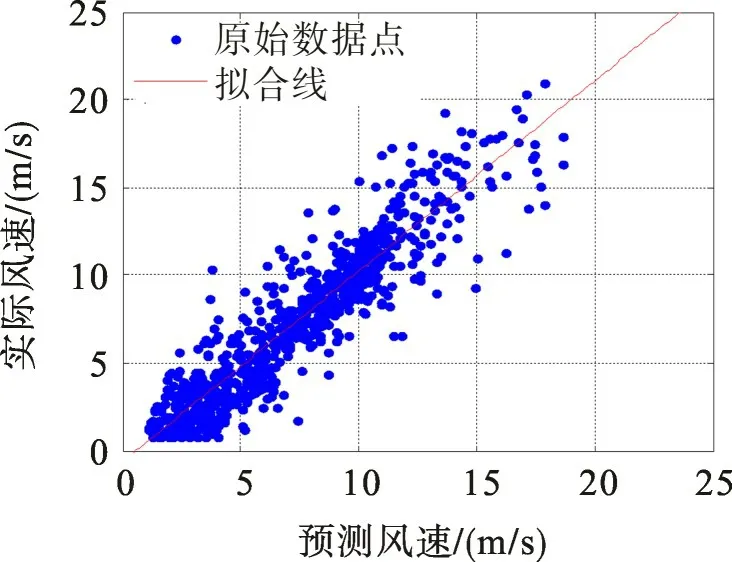
图6 校正后散点图Fig.6 Scatter after correction
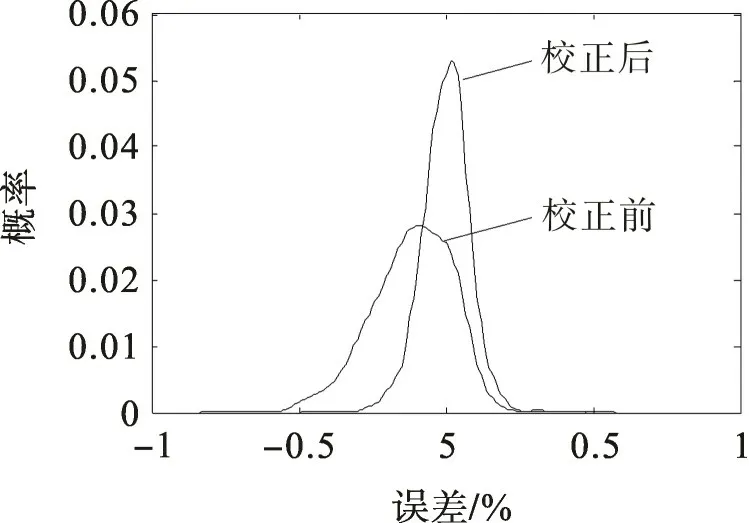
图7 误差概率密度曲线Fig.7 Probability density curves of error
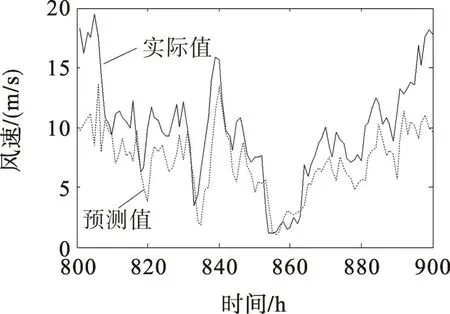
图8 校正前预测曲线Fig.8 Prediction curves before correction
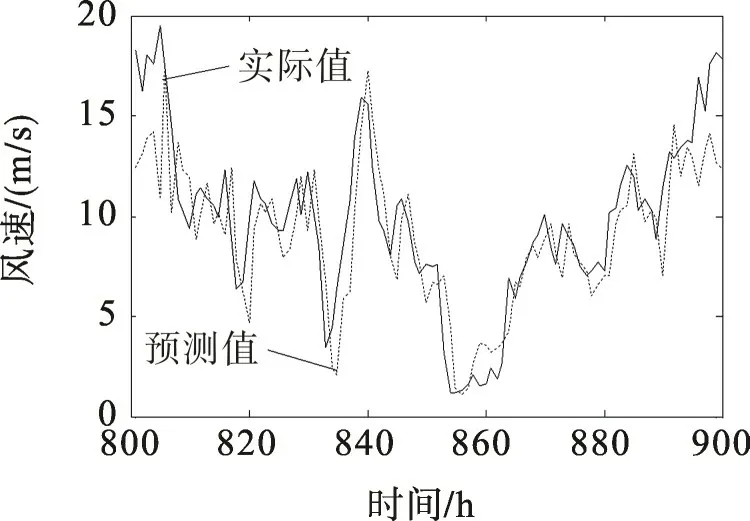
图9 校正后预测曲线Fig.9 Prediction curves after correction
4 结 论
1)WNN具有多分辨率局部时频特性,能够很好地逼近高维空间函数,但其参数的优化选择是关键。提出的二阶振荡粒子群算法在WNN参数优化中能够提高群体的多样性和全局收敛性,比基本粒子群算法更易得到全局最优解。
2)模型误差与模型复杂度具有较为密切的关系,模型误差的存在导致风速预测值偏离实际值,采用一阶线性回归法能够对风速预测结果进行校正,从而降低模型误差,提高风速预测精度。
