一种基于传统PI控制的PWM整流器新型双闭环控制策略
2019-03-31郎佳红张为民马振亚郑诗程
郎佳红,李 浩,张为民,舒 莹,马振亚,郑诗程
(1.安徽工业大学电气与信息工程学院,安徽马鞍山243032;2.合肥为民电源有限公司,安徽合肥230000)
三相电压源型PWM(pulse width modulation)整流器(voltage-source rectifier,VSR)具有输出电流畸变率小、可双向流动的能量、连网侧功率因数较高以及输出侧电压调节范围宽等优点,从而得到现代电力电子领域学者的重视,且在一些新兴工业领域得到广泛应用,如绿色发电(风力、光伏等)、不间断电源(uninterruptible power supply,UPS)和新兴混合动力车充电站等[1-5]。三相PWM整流器中常用的控制方法为线性控制方法以及非线性控制方法,非线性控制理论的提出促使滑模控制、模型预测控制以及无源控制等非线性控制方法应用于整流器系统中,且使系统的各方面性能更佳[6-12]。传统PI(proportional integral,PI)控制方法设计简单,是最常用的线性控制方法,也是当前技术比较成熟的控制方法之一,但其在两相静止坐标系下很难完成对电压交流量的无静差跟踪,且动态响应性能较差。滑模变结构控制是一种非线性控制,应用其控制PWM控制器可有效抑制谐波和负载波动的干扰,具有动态响应快、强鲁棒性的优点,但因系统惯性和控制能量等因素,直流侧电压会产生抖动[13-15]。
为进一步改善PI 控制方法的性能,杨勇等[16]提出直接功率控制策略(direct power control,DPC),即一种基于瞬时功率理论的PWM整流器控制策略,根据功率滞环比较器的实际输出对照开关表,进而确定合适的矢量控制方法实现对有功功率和无功功率的解耦控制,该方法设计算法简单、动态响应性能快速,但其所需的开关频率不恒定,对系统的采样频率要求很高,不利于系统稳定;陈强等[17]提出了一种改进型直接功率控制策略(direct power control,DPC),使用一种空间矢量脉宽调制(space vector pulse width modulation,SVPWM)方法实现对目标电压矢量的实时控制,该策略电流谐波畸变率较低及对直流侧电压的利用率较高,且其开关频率恒定,系统的稳定性较好,但电网电压角度信息不准确、电网电压出现畸变以及电网中谐波成分较多时对控制性能有很大影响,引起系统不稳定。为降低电压谐波以及电流纹波对磁链观测的影响,程鹏等[18]提出了一种固定开关频率虚拟磁链定向DPC(VF-DPC)策略,但该策略存在积分漂移问题,对电网电压矢量定向的准确度造成一定影响,其中PI和积分部分的引入使系统的跟踪性能有所降低;王良凯等[19]设计了一种基于滑模变结构PR控制的PWM整流器,有效解决了PI控制器在负载突变和起动时对电流内环参考指令跟踪调节速度慢、存在静态误差等问题。但在电网电压发生畸变时,无法有效抑制电流扰动,电网侧电流的总谐波失真(total harmonic distortion,THD)含量显著增加[20-25]。支琴等[26]提出了一种基于比例积分谐振调节的光伏并网逆变器电流控制方法,当电网电压发生畸变时,该方法能有效抑制电流扰动,电网侧电流THD含量较小,最终能达到并网的目的,但其使用的算法过于复杂,增加了系统的计算量。在此基础上,文中以电压型PWM整流器数学模型为基础,提出一种新型双闭环控制策略,在传统的控制策略基础上增加电流指令计算的新方法,以期较好地解决传统VSR电流闭环的矢量控制策略动态响应较慢和对抗干扰性能差的问题。
1 三相电压源型PWM整流器拓扑结构及数学模型
三相电压源型PWM整流器主电路拓扑结构如图1。图中:网侧输入电压ea,eb和ec采用三相对称无中性线连接方式;ia,ib和ic为三相输入电流;L为滤波电感;R为交流侧等效电阻;vdc为直流侧输出电压;RL为直流侧等效负载;iL为负载电流。为简化系统结构,假设所有功率开关器件均为理想元件,开关频率远大于网侧基波频率。
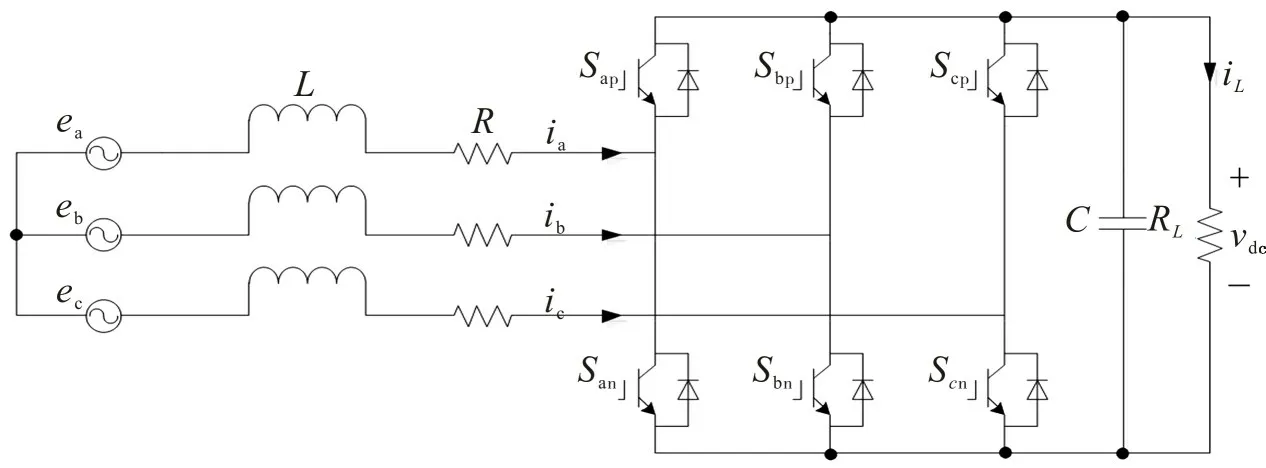
图1 三相电压源型PWM整流器主电路结构Fig.1 Main circuit structure of three-phase voltage-source PWM rectifier
三相电压源型PWM整流器在三相静止坐标系下的数学模型为:
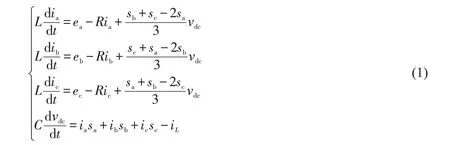
其中sa,sb,sc各相桥臂开关管的单极性二值逻辑状态,表达式为:sk=1 时,VSR的上桥臂导通,下桥臂关断;sk=-1时,VSR的下桥臂导通,上桥臂关断,(k ∈{a,b,c})。
将PWM整流器由三相静止坐标系变换到两相静止坐标系,其数学模型为:

式中:eα,eβ为坐标系下的网侧电压;iα,iβ为坐标系下的网侧电流;vα,vβ为坐标系下的开关管两端电压。vα,vβ与开关状态的关系可以表示为:

由两相静止坐标系αβ 经Park变换到旋转坐标系dq 下的数学模型为:
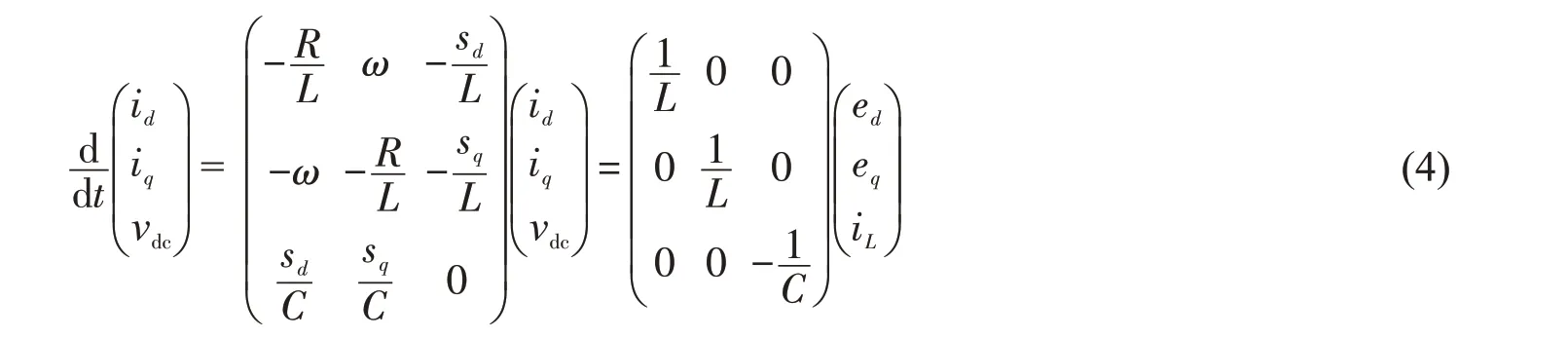
式中:ed,eq为相电压;id,iq为相电流;sd,sq分别为开关函数在dq 坐标系下的变量。
2 新型双闭环控制策略
如图2所示,根据三相电压源型PWM整流器的数学方程式,推导出两相旋转dq 坐标系下的控制模型,在传统PI控制的基础上,加入电流指令计算模块。以整流侧的直流母线电压为外环,通过PI调节,得到输出有功功率的给定值Pref;将Pref和无功功率给定值Qref通过电流指令计算模块得到有功电流指令值和无功电流指令值;再将和通过式(14)进行解耦控制得到和;将和通过同步旋转坐标变换,转换到两相αβ 静止坐标系上并得到和;最后通过SVPWM产生六路PWM信号控制VSR运行。
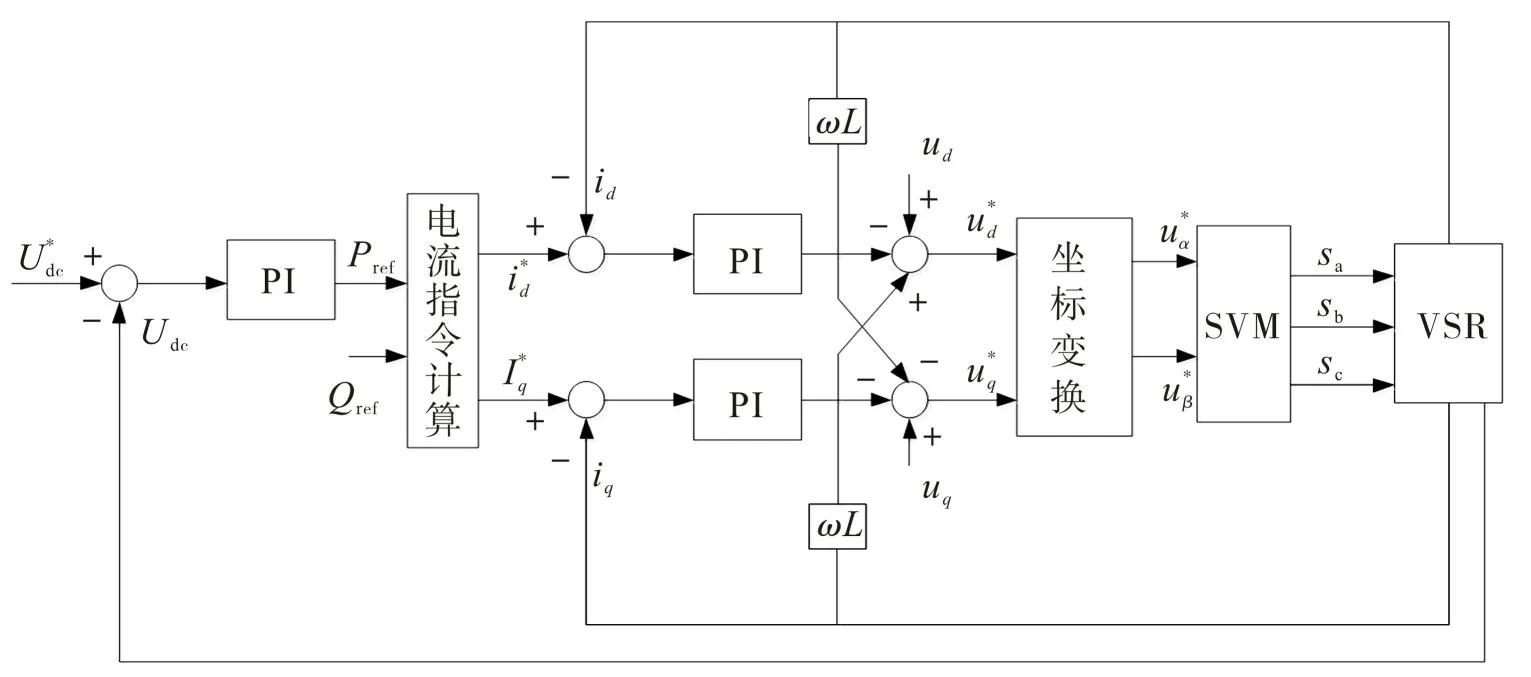
图2 三相电压源型PWM整流器控制系统框图Fig.2 Control system block diagram of three-phase voltage-source PWM rectifier
2.1 电压外环控制器的设计
电压外环控制结构如图3所示。电压外环控制的目的是保持直流侧电压Udc稳定。图中:τv为电压环采样时间常数;T 为电流内环的采样周期;Kv,Tv分别为电压环PI控制器比例、积分系数;m,θ 分别为VSR的调制比与开关函数初始相位角;iL为负载电流扰动;Wci(s)为电流闭环函数。

图3 电压外环控制结构图Fig.3 Structure diagram of voltage outer loop control
Wci(s)其闭环函数表达式可近似为

如图3所示,0.75m cos θ 为时变系数,对系统参数整定造成一定的影响。因VSR调制比m<1,时变系数0.75m cos θ <0.75,且因增益最大时其对VSR控制系统的影响最大,故用0.75取代时变系数进行分析。在此基础上忽略负载电流iL的影响,并且把电压外环小惯性时间常数τv和电流闭环等效时间常数3T 相加,得到Tev=τv+3T。简化后的电压控制结构如图4所示。

图4 简化后的电压控制结构图Fig.4 Structure diagram of simplified voltage control
由图4可知,其开环传递函数为

由于典型Ⅱ型系统有较强的鲁棒性,为了保持VSR直流侧电压稳定运行,文中采用典型的Ⅱ型方案,得到VSR表达式,为

由式(7)得到中频带宽hv=Tv/Tev,为兼顾系统跟随特性与抗干扰特性,取中频带宽hv=5,代入式(6)中,得PI控制器的系数Tv,Kv:

此外,VSR 控制系统的截止频率为

当τv=T 时,Tv=hv(τv+3T)=20T,得到系统的截止频率和频带宽度:


2.2 电流指令计算模块
如图2所示,Pref是电流指令计算模块的有功功率输入值,来自于电压外环的输出;Qref是电流指令计算模块的无功功率给定值,此值常设定为0。VSR终端有功和无功功率的表达式为:


其中ud,uq分别是电网侧电压的d轴分量和q轴分量。
2.3 电流内环控制器的设计
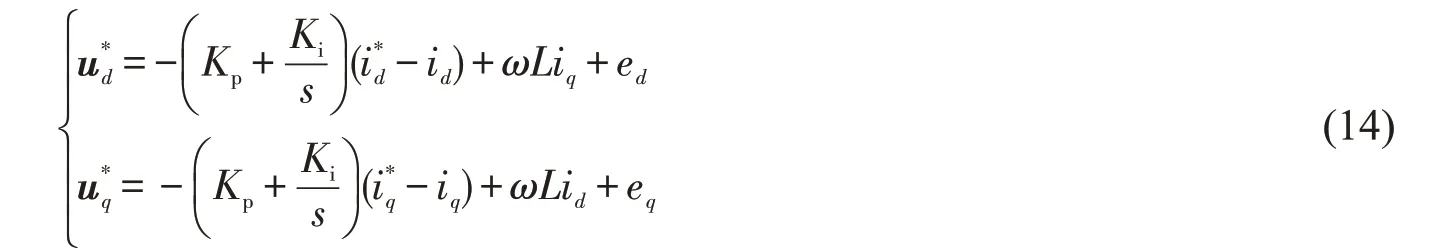
其中Kp,Ki分别为PI控制器的比例、积分增益。将式(14)代入式(13)可得
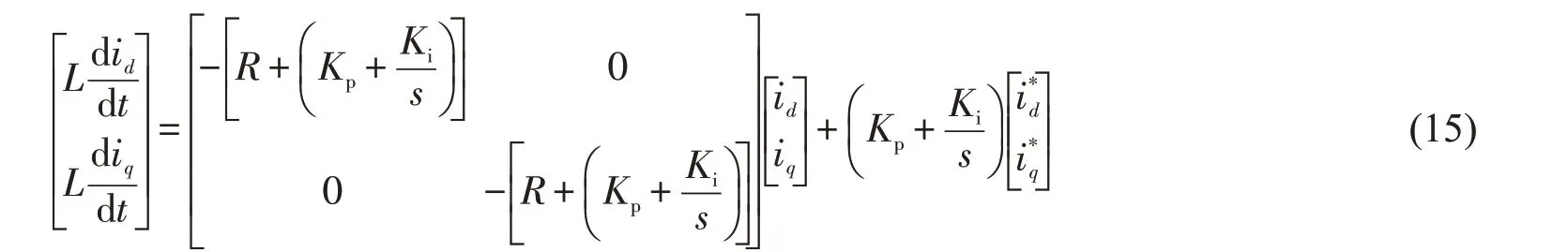
由式(15)可知,采用前馈控制可实现id,iq参数的解耦,且两者具有相同的控制结构,故以q轴参数为例进行分析设计。图5为iq的电流内环结构原理图。其中KPWM为VSR等效增益。

图5 电流环结构图Fig.5 Structure diagram of current loop
实际系统中,ωL ≫R(ω 为电流环截止频率),因此可忽略电阻R的影响,电流内环的简化结构图如图6。

图6 电流内环的简化结构图Fig.6 Simplified block diagram of current inner loop
图中,τ=Kp/Ki,若忽略电网电动势eq,其开环传递函数为

为改善VSR的运行性能,通常设置VSR中频带宽hi=τ/1.5T=5。典型的Ⅱ型系统关系式如式(17)

当中频带宽hi=5 时,由式(17)可得Kp,Ki的表达式为

3 仿真验证
以传统PI控制系统为基础,在MATLAB/Simulink环境下搭建新型双闭环控制仿真模型,并分别在启动、切载及电压变化的情况下对PWM整流系统交流侧电流THD值、稳态性能和动态性能进行对比分析。
3.1 谐波含量
两种不同控制策略的电流谐波含量THD如图7。由图7可见:在传统PI控制策略下,由于内环采用电流控制,可对电流进行直接整定,因此谐波含量较小,在3.33%,基本满足要求;采用新型双闭环控制策略时,因通过电流指令计算环节降低了直流电压脉动,谐波含量较传统PI控制有所减小,为1.15%。
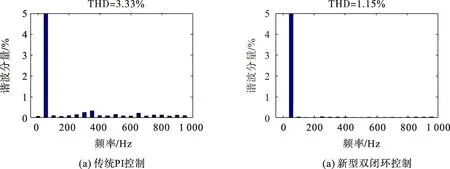
图7 两种控制策略下的电流谐波含量Fig.7 Current harmonic content under two control strategies
3.2 正常工作
图8为0.1 s时刻系统启动时两种不同控制策略的输出电压波形。由图8可知:采用传统PI控制策略时,电压出现超调,并且输出电压到达稳定值所需的时间较长,约0.05 s;采用新型双闭环控制策略时,输出电压到达稳定值所需的时间较短,只需0.02 s,且无超调,表明新型双闭环控制策略可有效提高系统的响应速度,使系统快速到达稳定状态。
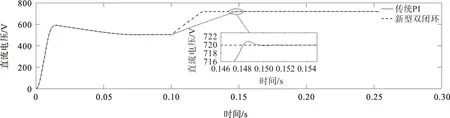
图8 直流侧电压输出波形Fig.8 Output waveform of DC side voltage
3.3 电压突升
图9为直流侧给定电压由720 V突然升至800 V时电压的跟随情况。由图9可知,在电压存在扰动的情况下,传统PI 控制策略的调节时间约21 ms,而新型双闭环控制策略的调节时间为10 ms。相比于传统PI控制策略,当再次达到稳态时,新型双闭环控制策略可使系统获得更快的动态响应速度,具有更好的抗干扰能力。
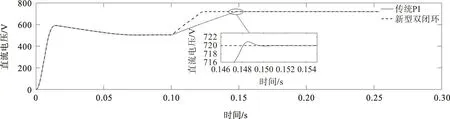
图9 直流侧电压突升后输出电压波形Fig.9 Output voltage waveform after DC side voltage surge
3.4 负载突变
图10为0.2 s时刻负载由200 Ω突降到100 Ω和100 Ω突增到200 Ω的仿真波形。由图10(a),(b)可知:采用传统PI控制时,系统动态响应较慢,直流电压跌落明显,约2 V;而采用新型双闭环控制时,系统不仅在额定负载时性能良好,且在负载突变时纹波脉动也很小,直流电压跌落较少,很快就能进入稳定状态。
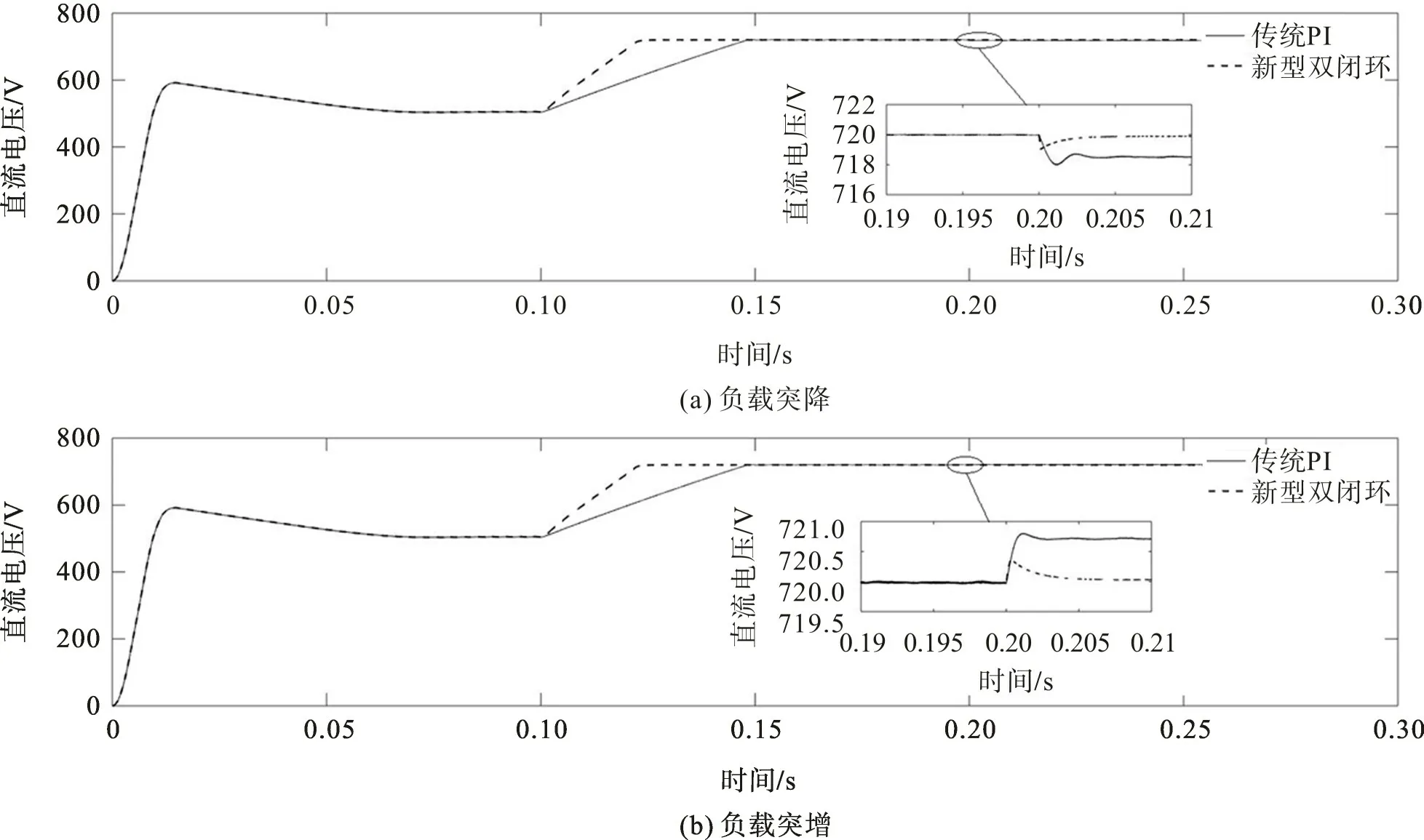
图10 负载突变时直流电压输出波形Fig.10 Output waveform of DC voltage during load sudden change
4 结 论
以三相电压源型PWM 整流器数学模型为基础,对传统PI控制策略进行改进,提出一种新型双闭环控制策略。仿真结果表明,当负载电阻和电压发生突变时,系统具有良好的动态性能,从而克服了传统PI控制策略动态响应较慢、稳态性能较差及当负载变化和电压变化等扰动时的抗干扰性能差等问题。
