一类5阶KdV方程的孤立波解

周兰锁,尹晓军

(内蒙古农业大学理学院,内蒙古 呼和浩特010018)

1.引言

自从1834年,Russell首次观察到孤立波以来,孤立子作为非线性科学的重要组成部分已经渗透到了许多研究领域,主要分布在应用数学、物理学、力学、大气和海洋科学等交叉学科领域里[1−3].

近年来,非线性方程发展作为孤立子理论的载体一直是数学物理工作者研究的热点,主要寻求非线性方程的孤立子解以及解的适定性问题.目前对于非线性方程的求解方法已经有很多,如:Jacobi椭圆函数展开法[4],同伦摄动法[5],齐次平衡法[6],B¨acklund变换法[7],Hirota双线性方法[8],Darboux 变换法[9],Sine-Cosine展开法[10−11]等.这些方法是求解非线性方程精确解的重要方法.但是,由于非线性方程的复杂性,至今没有统一的求解方法.1895 年,Korteweg和他的学生de Vries研究浅水波运动,推导出KdV方程并求得了精确解以来,KdV方程就被视为非线性数学物理的基本模型之一.后来,人们陆续在各个不同学科的实际背景下提出许多非线性偏微分方程,如mKdV,ZK,Schrdinger以及ZK-mZK方程等[12−15].

本文主要寻找一类5阶KdV方程

的孤立波解,这里α,β,γ是任意非零常数,其中uxxx,uxxxxx表示色散项.当方程系数为(α,β,γ) = (30,20,10),(120,40,20),(270,60,30) 时,称为Lax方程[16−17],它广泛应用于量子力学、流体力学以及等离子体物理领域中.对于5阶KdV方程,文[18]采用Jacobi椭圆函数展开法,获得了5阶KdV方程的一些精确解.文[19]利用Hirota双线性方法研究了(2+1)维广义5阶KdV方程的单孤立子解以及双孤立子解.文[20]根据Jost解的相容性原理,给出了求解高阶KdV方程孤立子解的一种简单方法.这里我们主要应用Sine-Cosine展开法去求解方程(1.1)的孤立波解.首先通过行波变换,把方程(1.1) 转化成一个5阶非线性常微分方程,然后经过正余弦函数的代数运算求得方程(1.1)的孤立波解,并把所得结果分别应用到Lax方程,SK方程,CDG方程中.

2.Sine-Cosine展开法的描述

假设偏微分方程

其中u(x,t)关于空间x和时间t的函数.这里,我们应用Sine-Cosine方法求解.

首先,为了求解方程(2.1)的孤立波解,我们引入行波变换

于是

根据(2.3)式,我们有下面的变换

应用(2.4)可把偏微分方程(2.1)变成下面的常微分方程

这里uξ表示

其次,我们尽可能多次地对常微分方程(2.5)求积分,并且把积分常数设置为零.假设方程(2.5)有如下的解的形式

或者形如

这里λ,µ和m是有待确定的参数,其中µ是波数,c是波速.对函数(2.6)求有限次导数,可得

同理对函数(2.7)求有限次导数,得

然后,我们把(2.8)-(2.11)或(2.12)-(2.15)代入到化简的常微分方程(2.5)中来.通过(2.12)-(2.15)余弦函数项之间的平衡,或者使用(2.8)-(2.11)正弦函数项之间的平衡,最后通过代数计算来确定λ,µ和m的值,从而获得方程(2.1)的孤立波解.

3.方程的孤立波解

下面考虑5阶KdV方程

其中描述行波解是u(x,t).应用(2.3)和(2.4)变换,方程(3.1)可变为

对上述方程积分,并令常数为零,可得

把(2.12)-(2.15)式代入到(3.3)式,整理可得

根据余弦项之间的平衡,对比方程(3.4)中的余弦项次数,得

即

把m=−2 带入方程(3.4)中,整理可得

令方程(3.7)中余弦项的系数为零,可得

解方程组(3.8)得

因此,方程(3.1)的解为

或者,把(2.8)-(2.11)式代入到(3.1)式,同理可得方程(3.1)的解为

其中ξ=x −16µ4t.

设µ=iµ1,那么(3.11)式变为

或者(3.12)式变为

其中ξ=x −16µ41t.

图3.1 方程(3.13)所表示的孤立波解,系数为:µ1 = 14,β =2,γ =2

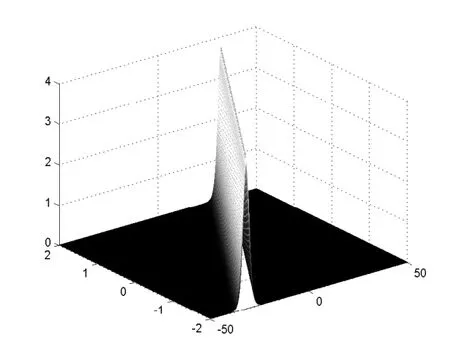
图3.2 方程(3.13)所表示的孤立波解,系数为:µ1 =−12,β =2,γ =2

下面我们具体讨论三种方程的孤立波解:

令γ=10 得Lax方程[16]

方程(3.16)的孤立波解为

或者

其中ξ=x −16µ41t.

b) 当β=γ,α=51γ2时,方程(1.1)为

令γ=5 得Sawada-Kotera(SK)方程[21]

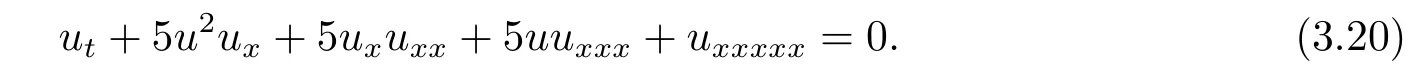
方程(3.20)的孤立波解为

或者

其中ξ=x −16µ41t.

c) 当β=γ,α=15γ2时,方程(1.1)为

令γ=30 得Caudrey-Dodd-Gibbon方程(CDG)[22]

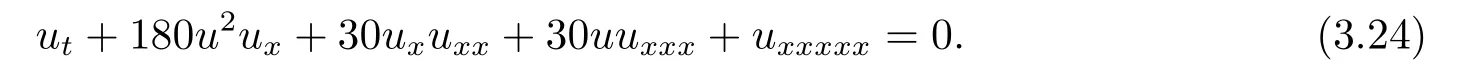
方程(3.24)的孤立波解为

或者

其中ξ=x −16µ41t.

4.小结

本文主要对一类5阶KdV方程的解析解进行了研究.应用Sine-Cosine展开法对具有一般性的5阶KdV方程求解,通过分别比较余弦项(正弦项)的次数和系数,得出了一类5阶KdV方程的孤立波解.然后应用所得的结果相应地得到了三种方程: Lax方程,Sawada-Kotera方程,Caudrey-Dodd-Gibbon方程的孤立波解,其结果扩充了5阶KdV方程解的结构.