基于ANSYSworkbench轮轴过盈装配过程分析

孙林平，伍世云，杨丽萍，王 贵

（四川文理学院 智能制造学院，四川 达州635000）

1 引言

无键的过盈配合常常用于高速旋转主轴中传递扭矩和轴向载荷，过盈配合属于高度非线性问题，传统依靠厚壁筒的理论公式进行计算，同时借助于有限元对其仿真.

有些研究利用ANSYS参数化对轴套过盈配合进行分析过盈量、弹性模量、内外径、摩擦因数等对接触压力在轴向上分布的影响规律，并总结出代数关系式，方便进行计算.［1－3］有些研究利用有限元分析平台分析轮轴接触压力和拔出力，通过参数综合，总结出过盈力与设计参数之间的关系方程.［4－5］有些研究建立了高速旋转主轴与转子额过盈配合模型数值模拟过盈量、旋转速度对过盈配合面间的应力、位移、接触应力的影响.［6－8］

本文从ANSYS workbench平台入手，对过盈配合的接触状态进行分析；并对其拆卸过程进行仿真研究，表明过盈配合是不适合拆卸后再使用.

2 过盈连接相关计算

主轴过盈配合设计主要从材料失效和防止结合面的滑动两个部分考虑，根据外界需传递的扭矩、承受的轴向载荷等因素计算所需的最小接触应力Pmin：

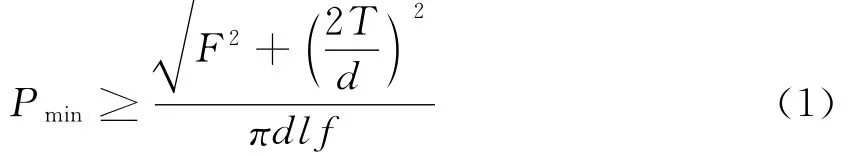
式中：F—轴向力，N；T—转矩，N.m；d—公称直径，mm；l—配合长度，mm；f—摩擦系数.

则最小过盈量：

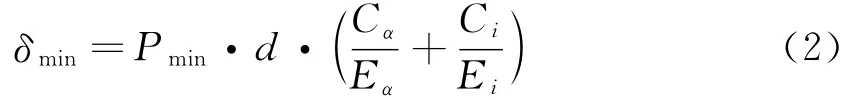
式中：Eα—包容件弹性模量；Ei—被包容件弹性模量；Cα，Ci—刚性系数νi—泊松比.

根据被连接件不产生塑性变形所应许最大结合面压力Pmax：

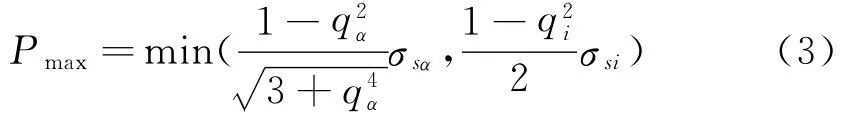
式中：σsα，σsi—材料屈服极限，MPa；

则最大过盈量：

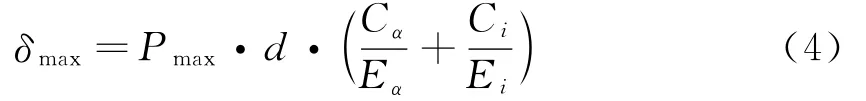
根据δmax，δmin选取公差配合.

3 仿真分析

3.1 模型的建立（过盈情况下的应力与拆卸应力）

由于轴对称，采用1／4作为研究对象对其进行建模，如图1所示，网格划分采用扫描网格（图2），共计约28000个节点.

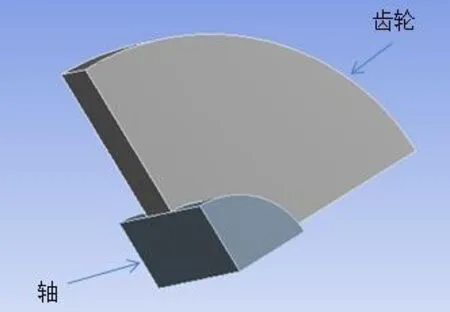
图1 模型

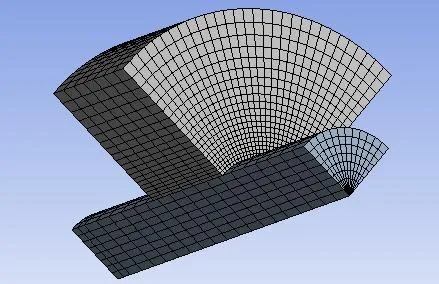
图2 网格划分

3.2 边界条件

在其端面施加对称约束，摩擦系数取0.2，过盈量设置为20um，本次分析共采用2个分析步，第一个分析步为静态分析步（3s），第二个分析步为将齿轮外端面固定，给轴施加轴向位移50mm.

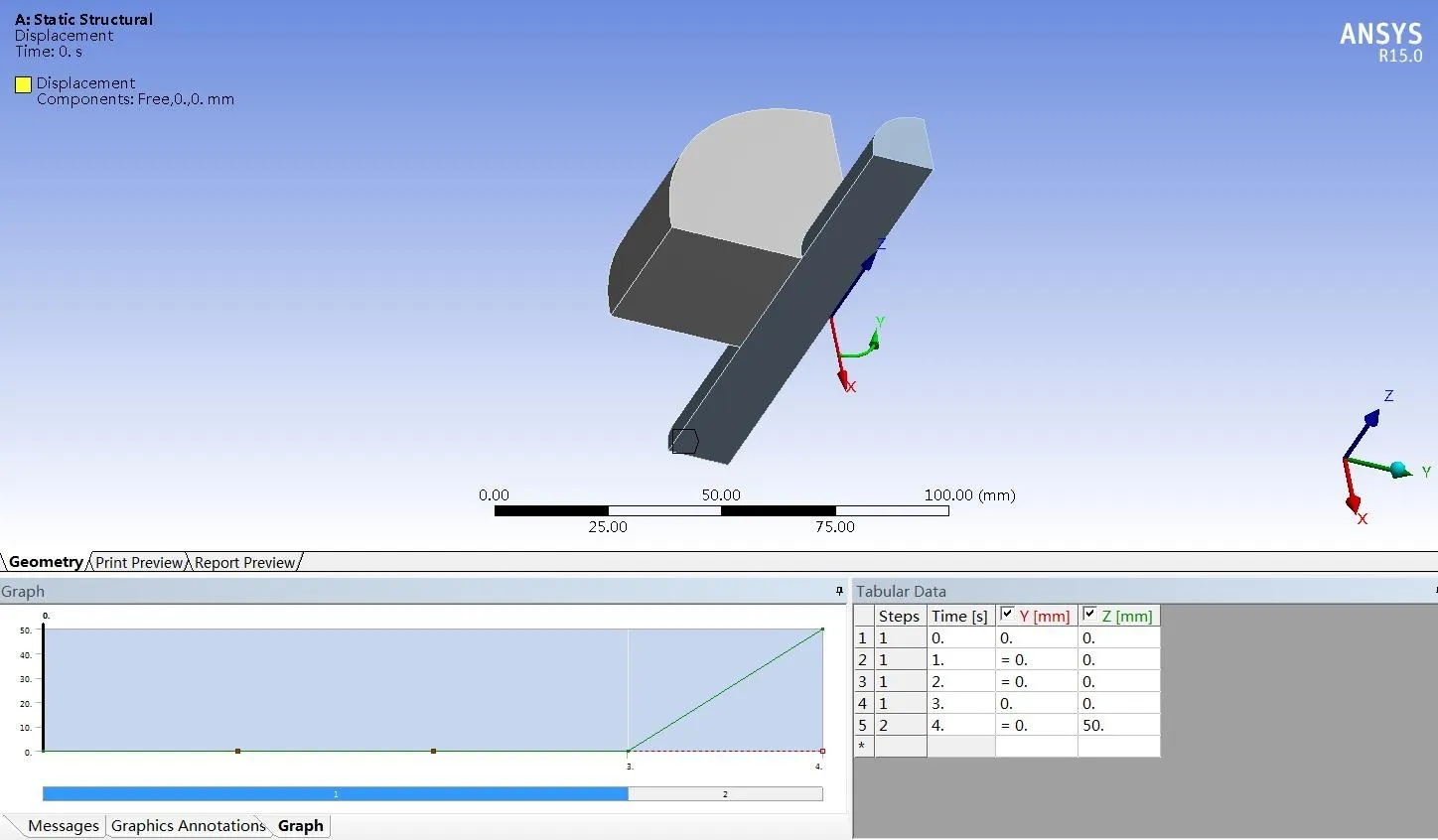
图3 边界条件设置

3.3 结果分析

（1）过盈情况下的应力、沿路径应力分布

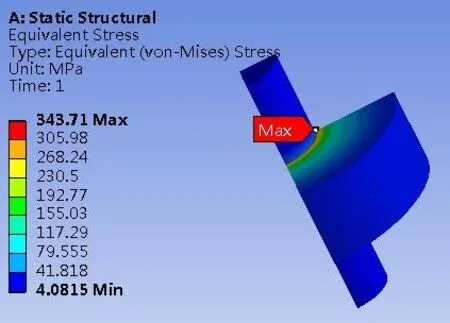
图4 Mises应力云图

图5 接触压力分布

从图4中可以看出在初始静态情况下的最大应力出现在齿轮的内孔边缘，最大为343.7MPa，故建议此处应倒圆角，减下应力.图5中为静态情况下接触面的接触压力，其最大接触压力为188.4 MPa，也出现在齿轮的内孔边缘.

沿路径上应力分布情况：

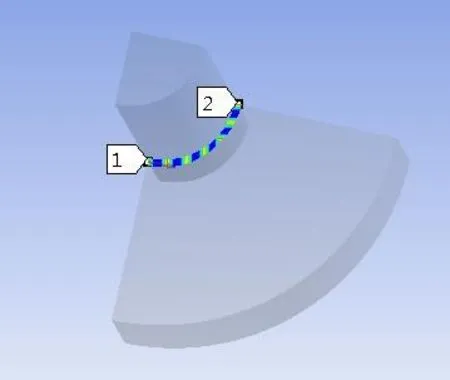
图6 圆环路径

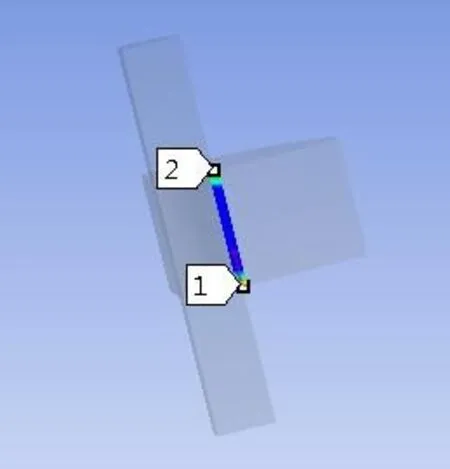
图7 轴向路径

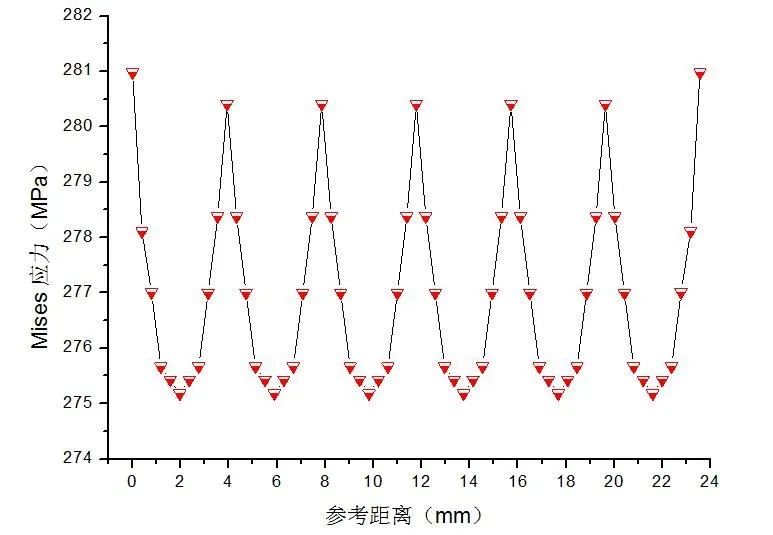
图8 圆环路径上的应力分布

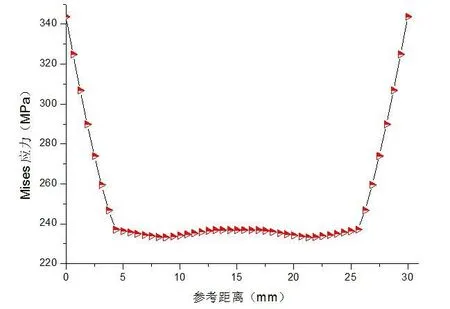
图9 轴向路径上的应力分布

图6 的路径为齿轮内孔的圆环，从图8中可以得出：Mises应力在此路径上呈整荡起伏循环状态，其值约在275MPa到281MPa之间，变化幅度不大；图7的路径为齿轮内孔轴向方向，图8可以得出Mises应力沿此路径呈U型分布，在两端处应力比较集中约为340MPa，在中间位置应力分布较为均匀，约为238MPa.

（2）拆卸情况下的应力分布

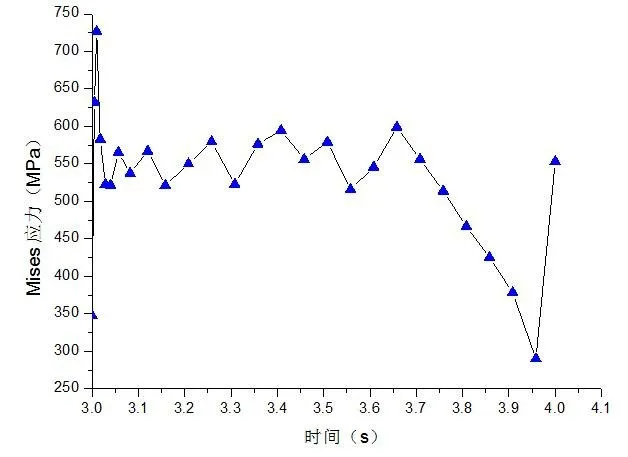
图10 拆卸应力—时间历程

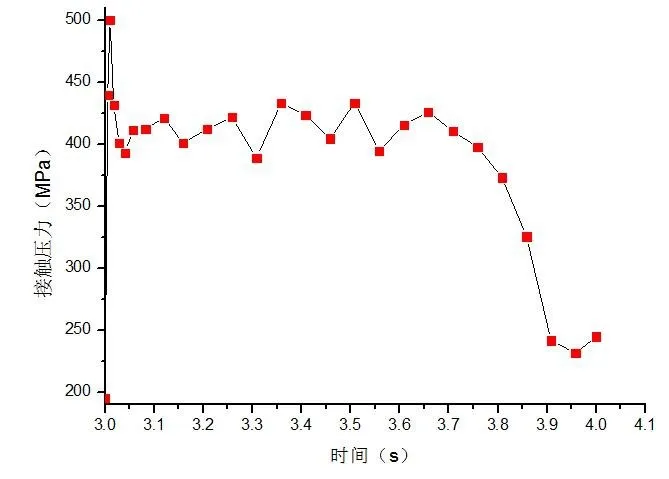
图11 拆卸过程接触压力—时间历程

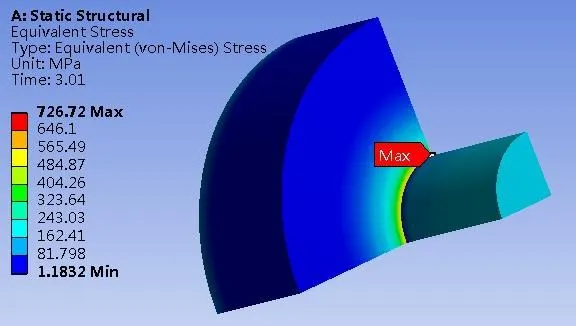
图12 拆卸过程中最大应力位置

图13 拆卸过程中接触压力最大位置

从图10可以看出拆卸过程中，Mises应力随着时间的增加出现大幅度的波动，其最大值约为726.7MPa，其位置如图12所示，已经远远超出了材料的许用应力［σ］＝460MPa，所以过盈装配作为一种典型的不可拆卸原理.图11为接触面上的接触压力时间历程，可以得出在拆卸的起始点接触压力较大约为499MPa，如图13所示，整个过程压力值波动后下降，但其最大接触压力也超出了材料的许用应力，在此证明过盈装配不适合拆卸后再使用.

结 论

（1）利用 ANSYS workbench平台对过盈装配的接触状态进行分析，配合面的最大Mises应力和接触压力都出现在内孔边缘，但处于安全范围之内；配合面的最大Mises应力沿圆环路径呈整荡起伏循环状态，但波动不大；沿轴向路径呈U型分布，两端应力值较大.

（2）分析过盈装配在拆卸的情况下，最大Mises应力、接触压力都出现了大幅度的波动，最大值都超过了材料的许用极限，表明过盈装配不适合拆卸后再使用.