椭圆方程间断有限元方法超收敛性的数值计算

张作政

(长沙学院计算机工程与应用数学学院，湖南长沙，410003)

1973年，REED和HILL首先在文献［1］中提出间断有限元方法求解中子输运方程。1997年，BASSI等［2］提出了一种求解可压缩Navier－Stokes方程的稳定的高阶收敛的DG格式。受BASSI和REBAY数值结果的启发，COCKBURN和SHU在文献［3］中提出了局部间断有限元(LDG)方法，与此同时，BAUMANN等［4］引入了一类新的DG方法。在文献［5］中，ARNOLD等人建立了基于九种不同数值通量的DG方法的统一框架。

近些年，DG方法被应用于求解椭圆形方程，并已经得到一些超收敛结果。CASTILLO在文献［6］中证明了一致且守恒的DG方法，数值通量在节点处是准确成立的，且在Gauss点处导数的超收敛阶为O(hp+1)。后来LARSON等［7］证明了在一致网格下使用IP－DG方法和NIPG－DG方法在节点处的数值通量均是准确的。2007年，XIE等［8］证明了用LDG求解一维椭圆形方程两点边值问题时，数值通量和其导数在节点处均准确。在文献［9］中，CELIKER和COCKBURN研究了一类DG方法求解一维对流扩散问题的超收敛性质，证明了在网格节点处守恒的数值通量和导数的通量都有超收敛性质，并且对于相应的椭圆型方程，数值通量是准确的。2009年，ZHANG等［10］证明了DG方法求解一维对流扩散方程的一些超收敛结果。对于 LDG方法，U和Q的离散误差主项分别与每个单元的P+1阶右Radau和左Radau多项式成比例，即P+1阶右Radau点和左Radau点分别是U和Q的P+2阶超收敛点。YANG等［11］和CAO等［12］分别对一位线性抛物问题的LDG方法的超收敛进行了分析。2017年，CAO等［13］再次研究分析了含有高阶导数的偏微分方程的LDG方法的超收敛性。

全文从数值上验证了用LDG方法求解二维椭圆方程的一些超收敛结果，对节点处的数值流通量有2P+1阶的超收敛，而对单元内部的右Radau点有P+2阶超收敛。

1 椭圆方程LDG方法介绍

为简单起见，考虑下面经典椭圆方程模型

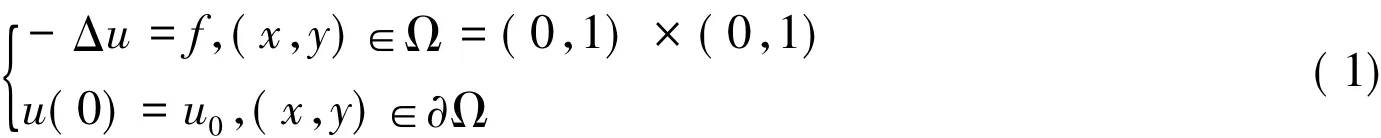
令q="u，则式(1)能够改写成下面的一阶方程组

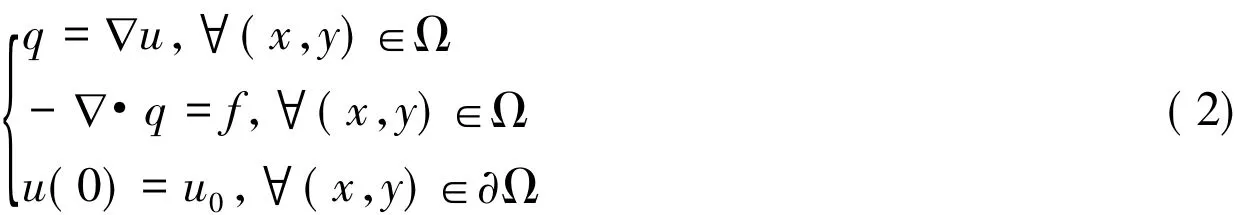
用任意试验函数r∈L2(Ω)2，v∈L2(Ω)，分别去乘式(2)的前2个方程，然后在Cartesian网格Τh的每个矩形单元k上分部积分，得

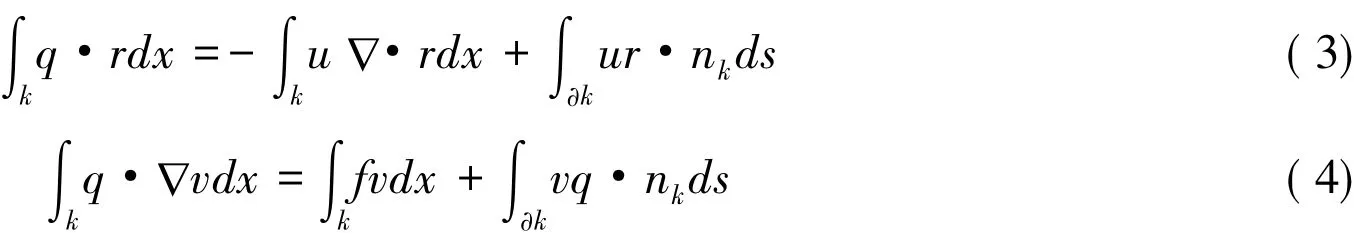
nk是k单位外法向量，定义有限元空间MN和VN如下:

其中S(k):=QP(k)={单元k上次数不超过p的多项式}。现在定义有限元解对应的弱形式，即寻找 qh∈MN，uh∈VN，使得对任意的 r∈MN，v∈VN，满足

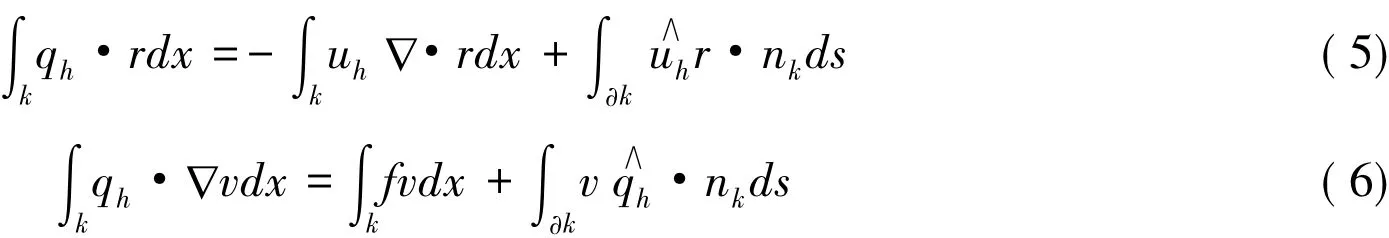
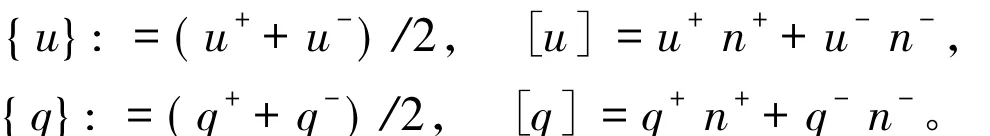
下面按文献［9］中LDG数值通量的取法，定义式(5)和式(6)中相应的数值流通量为若 e∈Τ0，则

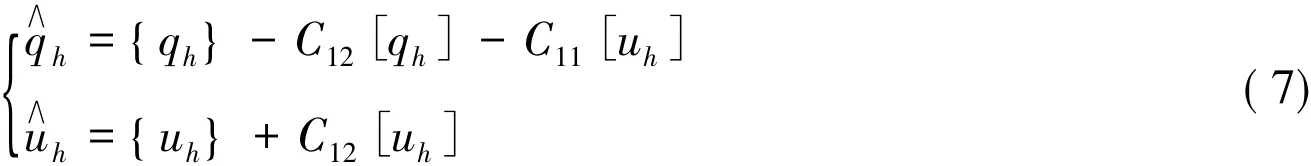
若 e∈Ω，则

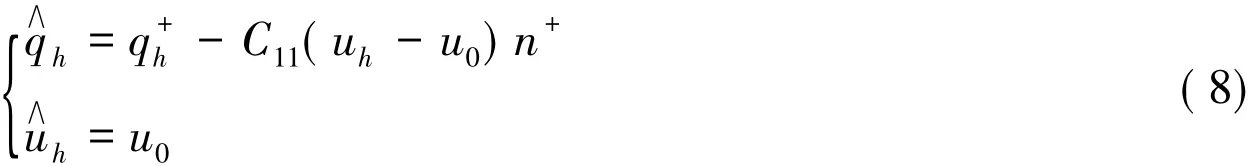
其中C11＞0是一个稳定参数，C11的取法既会影响数值格式的稳定性，又会影响数值方法的收敛速度。文献［9］对C11的影响作了详细的研究。在本文的数值算例中，取C11=1。C12是一个向量函数，满足 C12·n=sign(v·n)/2，其中 v= ［v1，v2］T，vi＞ 0(i=1，2) 是一常量。

2 椭圆方程LDG方法解的存在唯一性

定理2．1 考虑弱形式(5)和(6)定义的LDG方法，此时数值流通量按公式(7)、(8)定义，若 C11＞ 0，D11(i) ＞ 0，i=1，2，则对应公式(5)、(6)的数值解 (qh，uh)∈MN× VN是存在唯一的。

证明:由于模型问题(5)和(6)是线性问题，因此由唯一性就可以证得存在性。因此只需要证当f=0时，有qh=0和uh=0。

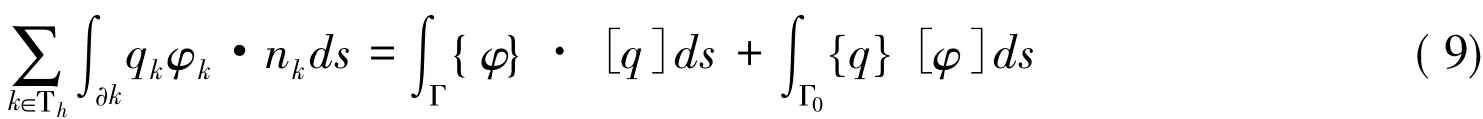
对式(5)关于所有单元k求和，并利用式(9)得

分部积分并再次利用式(9)得

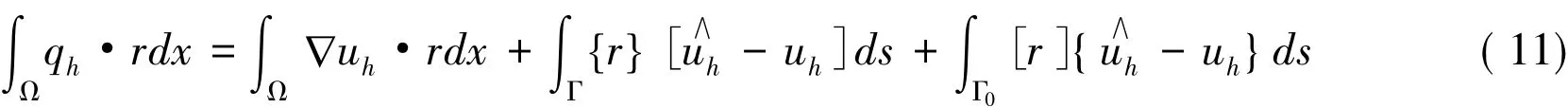
对式(6)关于所有单元k求和，并利用式(9)得

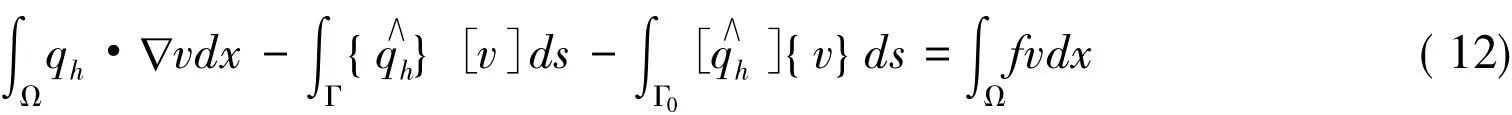
在式(11)和式(12)中，分别取r=qh和v=uh有

和

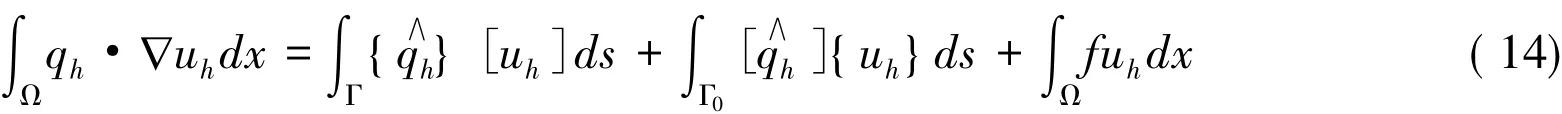
将式(14)代入式(13)，可得

记

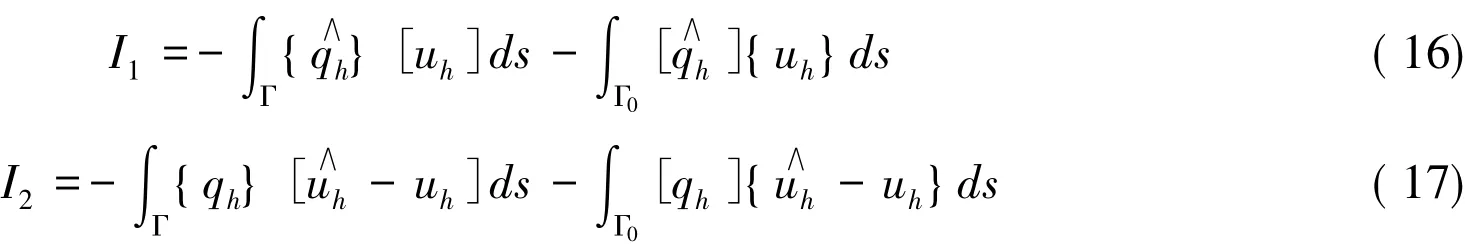
则式(15)能够写成

因为数值流通量的守恒性，则在Γ0上，有［］=0和［］=0，因此将式(7)、(8)代入式(19)得

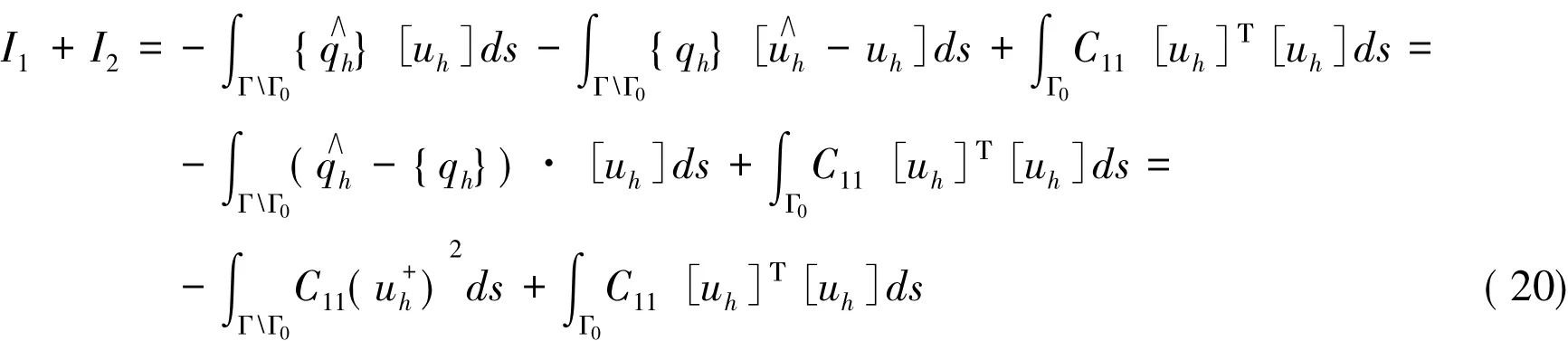
在定理2．1的假设条件下，在式(18)中，若f=0，则从式(18)和(20)，可以推出

将式(21)代入式(11)得

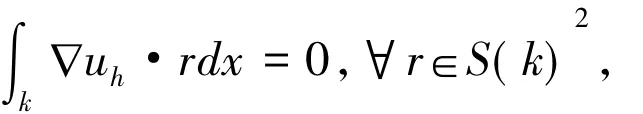
则在每个单元上"uh≡0，即uh为分片常数函数。又在Γ0上，［uh］≡0，且在Γ上，uh≡0，立刻推出uh≡0，定理2．1得证。

3 数值结果

考虑问题

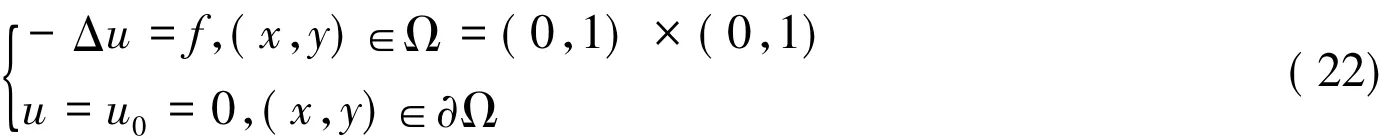
其真解为

在下表1中，‖u－U‖∞·*表示数值流通量的最大模误差;‖u－U‖R表示右Radau点处的最大模。从表中可以观察到U的L2模误差达到p+1阶丰满阶，在右Radau点处可以达到p+2阶超收敛，而数值通量处与一维问题相同，也达到了2p+1阶的超收敛。图1、3、5分别画出了p=1、2、3时的数值解U在一个单元上的整体误差图，图2、4、6分别是误差图对应的零级水平图，其中*表示右Radau点，从图中可以看到右Radau点都位于误差为零的曲线附近。

表1 md－LDG方法在矩形网格下的误差和收敛阶Table 1 The errors and superconvergence order on rectangle mesh for md－LDG

图1 U的误差零级水平图，p=1Fig．1 Zero－level curves of U，p=1

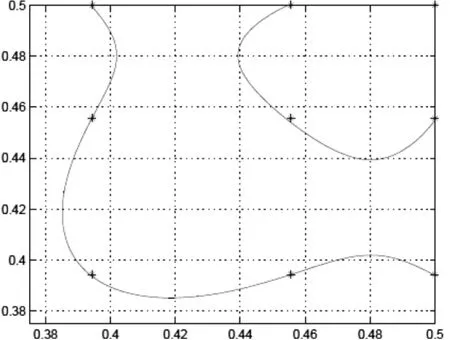
图3 U的误差零级水平图，p=2Fig．3 Zero－level curves of U，p=2

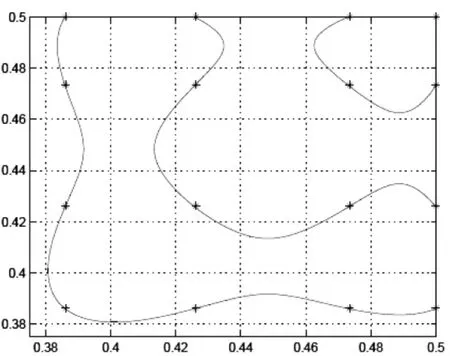
图5 U的误差零级水平图，p=3Fig．5 Zero－level curves of U，p=3

图2 U的误差图，p=1Fig．2 The errors of U，p=1

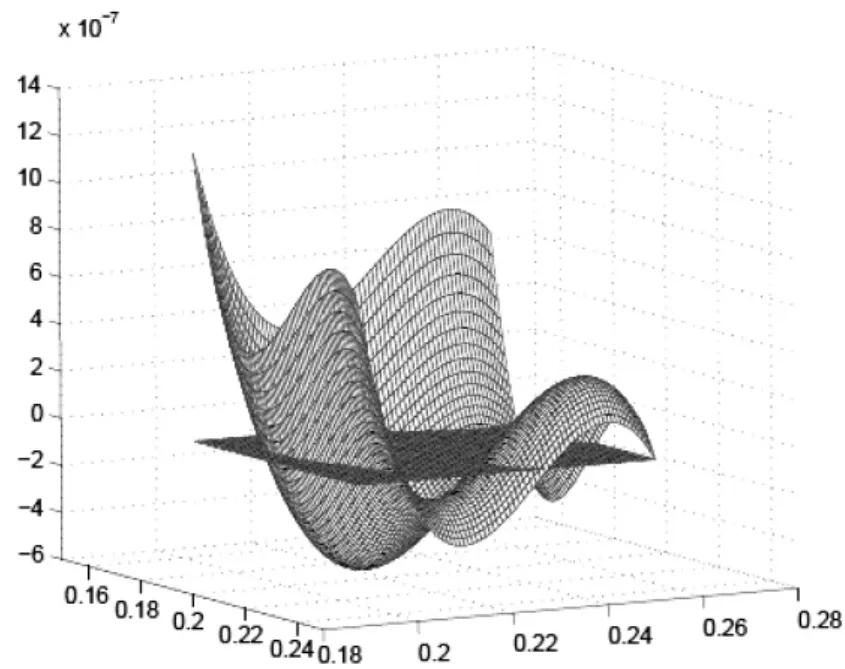
图4 U的误差图，p=2Fig．4 The errors of U，p=2

图6 U的误差图，p=3Fig．6 The errors of U，p=3