弱管制下两机冲突解脱策略

郭嘉

摘 要：文章研究弱管制环境下两架飞机冲突解脱策略。使用点质量级飞行模型且将两架飞机冲突解脱问题确定为非线性最优管制问题，同时选择性能指标，使得在满足最低间隔的条件下尽量减少两架飞机改航角度。

关键词：弱管制；冲突解脱；遗传算法；非线性最优管制；性能指标

中图分类号：TP391.9 文献标志码：A 文章编号：2095-2945（2019）04-0023-03

Abstract： This paper studies the conflict resolution strategies of two aircrafts under weak control. The point quality flight model is used and the two aircraft conflict resolutions are determined as deterministic nonlinear optimal control problems. Meanwhile， the performance indicators are selected， so as to minimize the diversion angle of the two aircrafts under the condition of meeting the minimum interval.

Keywords： weak control； conflict relief； genetic algorithm； nonlinear optimal control； performance index

在現行的空中交通管制[1]（Air Traffic Control）体系下，民航飞机都是按照地基导航系统所限定的由无线电信标建立起来的航线安排航班的，飞机必须沿着由一系列导航台组成的固定航路和飞行程序进行飞行。由于导航台这些设施不是全面覆盖的，因而飞机不能选取通往目的地的最直接路线，这导致航路交通日益拥挤，空域整体利用率不高。

对于这种状况，“弱管制”是一个有效的解决办法。即在一定飞行区域内，航空器运营人可以实时更改航线，只有当飞机之间存在潜在冲突时，管制员才介入指挥，能够最大限度地减少运营成本，从而提高经济效益。然而随着航空器数量的增加和自由航线的多样性选择将决定了飞机之间的冲突概率增大，尤其在低空空域[2]。因而研究两机之间冲突解脱策略是能否实现“自由飞行”的关键一环。

1 问题描述

在一个弱管制的空域，假设飞机以恒定的航向飞行。一般来说，这两架飞机将以相同的方式（左或右）转动大致相同的角度以避免冲突。然而，当相交角较小时，一架飞机需要采取伸展路径以避开另一架飞机。如果两架飞机的速度相同，那么任何一架飞机都可以执行路径拉伸。如果两架飞机的速度不同，较慢的飞机应该执行路径拉伸。

如果两架飞机发生冲突，即两者的间隔距离[3]低于最小规定值，而最低间隔要求取决于飞机类型、飞机位置确定的准确性和空中交通管理结构。成功的冲突解决策略取决于诸如改变飞机位置的方法等许多要素确定和空对空，空对地通信。本文提出一个系统自动化的观点，冲突解脱过程由飞机轨迹预测，冲突检测和估计冲突可能性，以及解决冲突的综合策略共同组成。本文确定了弱管制下两架飞机冲突解脱方案的最优模式。具体而言，潜在冲突的解脱方案被制定为非线性最优控制问题。假定两架参与潜在冲突的飞机都处于平飞状态，并使用飞机倾斜角度作为控制。选择性能指标是为了尽量减少两架相关飞机与其原先预期的飞行路径的偏差，或者最小化倾斜角度，并遵守最低间隔要求。此外，还包括终端限制，这些限制迫使两架飞机在避免潜在冲突后返回其原始飞行路径。

轨迹预测总是包含误差。一般来说，轨迹预测误差会随着时间而增长，特别是在纵向方向上。在一定量的“向前”时间（例如20至30分钟）之后，轨迹预测误差会在不可接受的范围内导致预测的轨迹不可用。

轨迹预测误差可以通过确定性最坏情况边界或作为随机过程来描述。在确定性框架中，例如：

e=k0+k1t+k2t，由于篇幅有限，假定当前论文中e=0进行简化分析，并基本认为完成了精准轨迹预测，这些结果在短时间内有效，可作为一般性的指南。

2.2 两架飞机冲突检测与解决

在目前的空中交通管制系统中，通过指定的航线实现航路横向间隔，通过不同的飞行高度层配备保证垂直间隔，用调整速度保证足够的纵向间隔。在最终下降阶段（接近终端区）时，速度变化也是保持间隔的主要手段，其次是高度变化和路径拉伸。

在弱管制飞行系统中，这三种控制方法都可用于冲突解脱：速度变化，高度变化和航向变化（路径拉伸）。在航路飞行阶段，航向变化对于产生长期失误距离最有效，而高度变化（爬升/下降）可以在很短的时间内提供足够的垂直间隔。由于巡航时飞行速度较高，变速效率最低[4]。在本文中，仅使用航向检测来研究冲突解脱方案。具有恒定速度的水平飞行中的飞机的点运动方程式是：

潜在冲突有两种基本类型。如果两架飞机在非常接近的时间内试图收敛到相同的航路点或跑道，则说冲突是目标冲突；如果两架飞机之间的间隔低于某个最低标准，则冲突被认为是最小间隔的损失。

目标冲突要求重新调整一架或两架飞机到达航路点或跑道的时间，如果目标冲突未得到解决，未来某个时间段最小间隔必然会产生损失。另一方面，参与航线最小间隔冲突损失的飞机可能在不影响预定到达时间的情况下解决冲突。在弱管制的途中阶段，最小间隔损失是主要关心的问题。然而，在过渡区域或终端区域，必须优先解决目标冲突。

2.3 冲突检测

考虑检测和解决两架飞机在航路飞行期间相距不超过2000英尺飞行高度的冲突。在冲突检测时间t0=0时，两架飞机都以恒定速度飞行并且跟随恒定航向角度。通过

目标冲突：

我们现在考虑两架飞机试图转向相同路线的情况。在数学上，具有指定标题的路线可以通过位置和标题来描述。如果两架飞机试图通过同一点（xf yf），则会在短时间发生目标冲突，对于指定的最终时间τf，从中确定最佳控制ψ1和ψ2， 其中Kμ1和Kμ2是正的权重，服从等式中的运动方程。

公式中的性能指标在机动过程中使倾斜角最小化。

4 结论

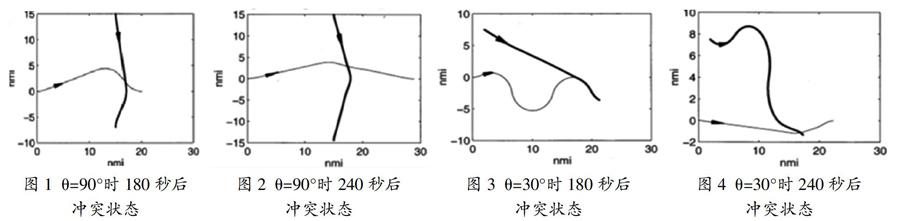
（1）如果相交角较大，那么涉及潜在冲突的两架飞机的最佳冲突解脱操纵方式是相似的，这两架飞机以相同的方式（左侧或右侧）转向，以避免潜在的冲突。每架飞机的轨迹大致由两条由目标点连接的直线路径组成。因此只需要确定每架飞机的目标点。（2）如果相交角较小，则最佳冲突解脱操纵方式要求一架飞机延迟其到达预测冲突点的时间，而另一架飞机遵循双直线路径。当两架飞机具有相同的速度时，任何一架飞机都可以执行路径拉伸以避开其他飞机。然而，当速度不相等时，较慢的飞机应该延伸其路径以延迟其到达预测的冲突点。（3）当两架飞机试图收敛到具有特定航向的相同航线时，一架飞机必须放慢速度以远离另一架飞机。

参考文献：

[1]杜实.空中交通监视服务[M].北京：中国民航出版社，2012.

[2]朱代武.低空空域飞行冲突避让算法[J].交通运输工程学报， 2005，5（03）.

[3]24 Holt， J. M.， and Marner， G. R.， "Separation Theoryin Air Traffic Control System Design，" Proceedingsof the IEEE， Vol. 58， No. 3， pp. 369-376. March，1970.

[4]Bergh， C. P.， Krzeczowski， K. J.， and Davis， T.J.， "TRACON Aircraft Arrival Planning and Optimizationthrough Spatial Constraint Satisfaction，"Air Traffic Control Quarterly， Vol. 3， No. 2， 1995，pp. 117-138.