动力显现巷道支护系统抗冲击能力的理论计算方法研究

2019-03-29刘少虹

采矿与岩层控制工程学报 2019年1期

刘少虹

(1.天地科技股份有限公司开采设计事业部，北京 100013；2.煤炭科学研究总院开采研究分院，北京 100013)

随着我国煤矿开采深度及强度的不断增大，冲击地压灾害数目逐年增多。而采场围岩的支护系统作为抵抗冲击地压发生的最后一道屏障，其作用至关重要。自2010年以来，内蒙平庄古山煤矿开始出现冲击地压灾害，其中最为严重的一次，工作面上下两巷均出现垮塌。事故发生后，古山矿优化了支护方式，效果较为显著。

关于采场围岩支护的研究，康红普，王金华[1]建立了煤巷锚杆支护理论与成套技术；鞠文君[2]分析了冲击矿压巷道锚杆支护原理；潘俊锋等[3-4]将支护结构纳入到冲击地压发生机理中，建立了冲击地压启动理论；吴拥政，林健等[5-6]通过优化支护构件及材质，提升了围岩整体的支护质量；潘一山等[7]提出了“提高支护刚度和快速吸能让位支护”等冲击地压矿井巷道支护设计思路，并由此开发了一种新型防冲吸能液压支架。王爱文等[8]建立了吸能支护围岩在冲击载荷作用下的力学模型，获得了支护锚杆顶板位移阻抗函数的解析公式；高明仕，窦林名等[9]分析了锚杆变形对震动波的适应性，并计算了锚网支护吸能防冲能力；王桂峰等[10]对巷道支护的防冲能力进行计算，并探讨微震反求支护参数方法的可行性。

综上所述，目前对于动力显现巷道支护系统抗冲击能力的定量计算方法的研究尚有不足，因而不能准确地比较支护方式间抵抗冲击地压能力的优劣。这里基于冲击启动理论，采用理论分析与数值模拟相结合，建立巷道支护系统抗冲击能力的计算方法，对于冲击地压治理具有重要现实意义。

1 支护系统抗冲击能力计算原理

1.1 冲击启动判据[3]

1.1.1 集中静载荷型冲击启动判据

巷道开挖后，两帮围岩内形成支承压力区。由广义虎克定理，三向受力状态下煤体弹性应变能计算公式为：

(1)

式中，E为弹性模量，Pa；μ为泊松比；σ1，σ2，σ3为三向主应力，Pa。

假设巷帮的极限平衡区处承载的弹性应变能为EΩ0，它是巷道围岩中弹性应变能极大值。通常为巷道煤帮主承载区发生失稳破坏，破坏条件是应力超过单轴抗压强度或抗剪强度即σ>σc或τ>τc，对应的能量消耗准则为

(2)

由此建立冲击启动能量判据为

EΩ0-Ec>0

(3)

式中，EΩ0为支承压力峰值区三向主应力，Pa，代入式(1)求解。

1.1.2 集中动载荷型冲击启动判据

集中动载荷型冲击启动受工作面超前支承压力和采场上覆坚硬顶板垮断共同影响。采场坚硬顶板断裂传递至煤壁极限平衡区的能量Ed由式(4)计算得：

Ed=Ed0R-η

(4)

式中，Ed0为顶板断裂时震源能量，J；R为顶板断裂震源至煤壁极限平衡区的距离，m；η为弹性波在煤岩介质中传播时能量衰减指数。

由此建立冲击启动能量判据为

E0+Ed-Ec>0

(5)

1.2 支护系统抗冲击能力计算原理

支护系统是阻挡冲击地压发生的最后一道屏障，从而“巷道围岩支护系统究竟能抵抗多大程度的冲击”就成为十分关键的问题，以下对支护系统的吸能防冲能力进行讨论。由上述冲击启动能量判据，当外部动、静载荷的能量大于系统自身破坏所消耗的能量时，冲击地压就会发生。因此，冲击地压发生主要由支护系统破坏消耗的能量Ec、支护系统内部蕴藏的弹性能E0以及支护系统受到的外部载荷能Et、冲出煤体所含有的动能4部分决定，以下对前两部分能量进行详细分析。

1.2.1 支护系统耗散能量分析[11]

首先来看支护系统耗散能Ec。为了对Ec进行计算，需要对支护能量进行分析，并引入能量守恒、转化以及弹性能做功理论。在冲击地压矿井混凝土喷层通常较薄，并不起承载作用，所吸收的能量也十分有限，这里忽略。支护系统就像在围岩表面存在着许多小弹簧，包括了支护材料与材料间的煤岩体，如图1所示。锚杆、索、网联合支护属于主动支护形式，能够对巷道围岩产生支护力Fs(Pa)，与支护材料之间煤岩体形成支护结构，且支护结构还受到其外部煤岩体对它的压力P(Pa)，如图1所示。

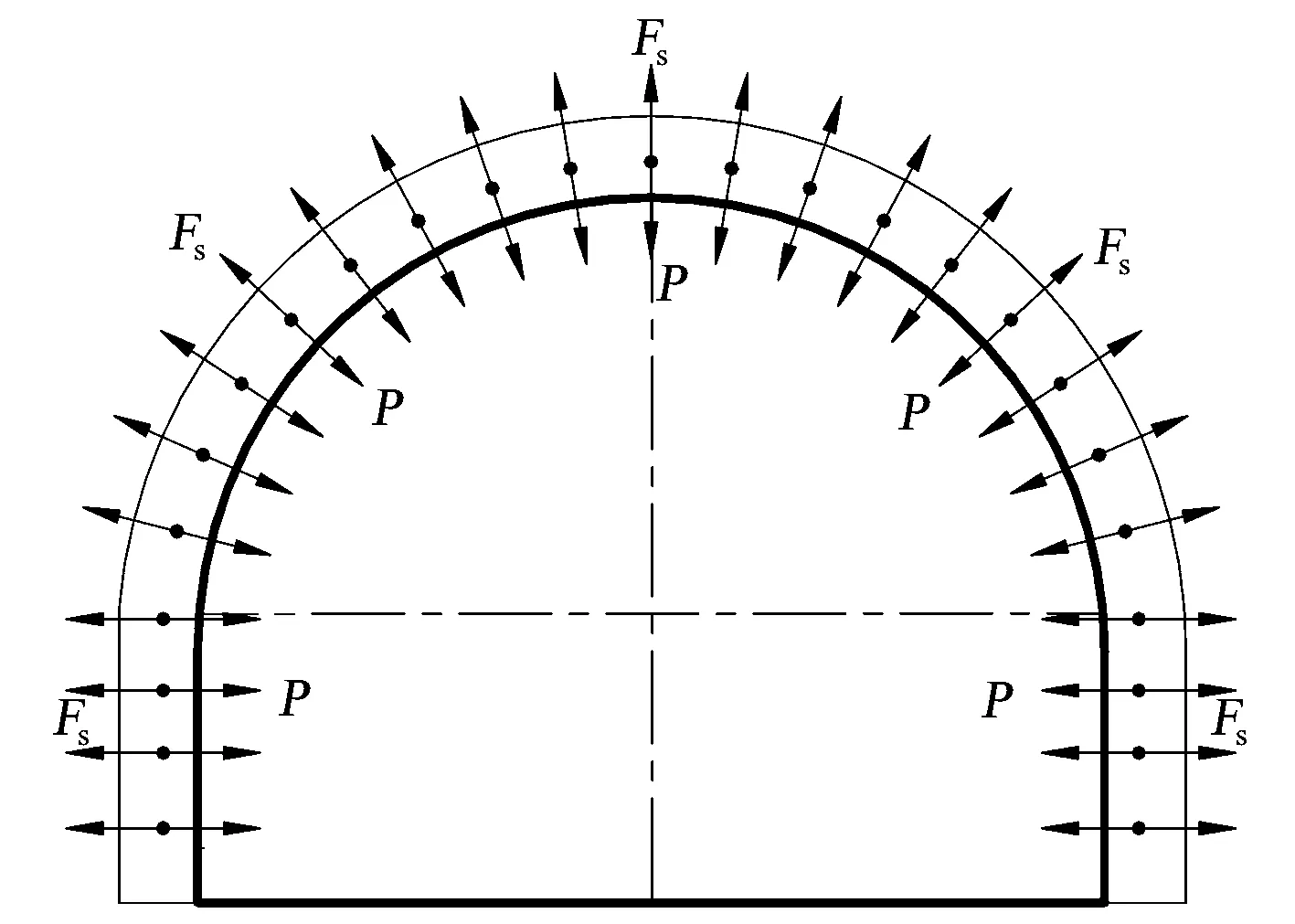
图1 支护结构力学模型

由于支护材料大多采用钢材质，发生塑性变形的过程较为短暂，认为支护材料在受拉超过其弹性变形极限后立即发生破断，即将冲击地压发生过程中，支护系统所消耗的能量Ec分为弹性变形和破断两部分加以考虑，如式(6)：

Ec=Wl+Wb+Wm

(6)

式中，Wl为支护结构变形耗能，J；Wb为支护材料破断耗能，J；Wm为煤岩体破坏耗能，J。

根据温克尔(Winkler)假设，支护结构受到的合力Ft为

Ft=P-Fs=ζΔ

(7)

式中，ζ为支护结构的刚性系数，Pa/m；Δ为支护结构的伸长量，m。

此时由于支护结构的受拉伸长所消耗的能量Wl为

dWl=Ftdx=(P-Fs)dx=ζxdx

(8)

由此可知，支护结构伸长变形所消耗的最大能量Wlmax为

(9)

由于岩石的抗压强度较低，则支护结构的刚性系数主要由钢质支护材料决定，由此可知

(10)

式中，Es为支护材料的弹性模量，Pa；As为支护材料的截面面积，m2；Lsf为支护材料的自由段长度，m。

而支护结构的最大伸长量Δmax，可由式(11)求得

Δmax=Lsfω

(11)

式中，ω为支护材料的延伸率，通常左旋无纵筋螺纹钢锚杆的延伸率按8%计算，而锚索的延伸率按6%计算[1]。

将式(10)、(11)分别代入式(9)整理得到，支护材料受拉发生弹性变形而消耗能量的表达式

(12)

式中，nl为支护材料的数目，根。

以上部分主要对变形阶段加以分析，接下来对支护材料在破断阶段所消耗的能量进行讨论。

冲击地压发生现场实际观察发现，冲击发生后支护材料大多被拉断，因此材料破断所消耗的能量Wb为

(13)

式中，σcs为支护材料的抗拉强度，Pa；Vb为支护材料自由段的体积，m3。

煤岩体破坏耗能Wm由式(14)求得

(14)

式中，σm为煤岩体的单轴抗拉强度，Pa；Em为煤岩体的弹性模量，Pa；Vm为冲出煤体的体积，m3。

最后，将式(12)、(13)、(14)代入式(6)可得支护系统耗散能Ec的计算公式

(15)

1.2.2 支护系统内部蕴藏弹性能分析

由冲击启动能量判据可知，集中动载荷型和集中静载荷型冲击地压外部能量源是不同的，但是无论哪种类型的冲击，在发生过程中支护结构本身不但消耗能量，而且其内部所蕴藏的弹性能Ei也必然会释放，这部分能量可由式(16)计算，其中弹性能密度ε可以通过将式(1)写入到FLAC3D中求得，如图2所示，以全锚索支护方案为例。

Ei=εVm

(16)

图2 全锚索支护方案下弹性能分布

1.2.3 冲击过程的能量转化关系

除了上述得出的支护结构内蕴藏的弹性能，冲击发生所需其他能量均来自于支护结构外的集中动载源或集中静载源，根据能量守恒定律得到冲击地压发生时的能量转化关系为

(17)

(18)

(19)

式中，Eu为支护系统受到的外部载荷能，J；Ey为冲出煤岩体具有的动能，J；Ec为支护系统的耗散能，J；v0为煤体冲出的初始速度，m/s。

由上式即可得到各支护形式巷道发生冲击所需的能量。

1.2.4 关于冲击范围的讨论

冲击地压的发生范围是另一个在计算巷道支护抗冲击能力的影响因素。事实上，冲击地压范围越小，冲击时支护系统对能量消耗的越小，从而对外部载荷能的需求就越小，冲击地压就越容易发生。按照冲击地压发生范围的大小分为轻度冲击和强烈冲击，本节首先对轻度冲击地压进行讨论，分析发生这种类型的冲击所需能量的大小，以及冲出煤体的最大初始速度。以此为基础，再对强烈冲击地压进行讨论。

首先看情况1，最为轻度的冲击地压是单根支护材料及其周围煤岩体的损坏，图3(a)为情况1的煤壁破坏范围示意图。此时，nl=1，Vm=4abdp，由式(19)可知，巷道临界冲击能量Eu的计算公式为

(20)

式中，a为支护材料的间距，m；b为支护材料的排距，m；dp为冲出煤体的深度，m。式(20)，当v0=0即是发生轻度冲击地压情况1的临界条件。

随着外部载荷能逐渐升高，煤体冲出的初始速度逐渐增大。当能量升高至可以将2根支护材料及其周围煤岩体同时破坏时，就进入情况2，图3(b)为情况2的煤壁破坏范围示意图。此时，nl=2，Vm=6abdp，由式(19)可知，巷道临界冲击能量Eu的计算公式为

(21)

注意到，式(21)中v0=0时，即是情况1和情况2之间的临界情况，这时将式(21)代入式(20)，进行整理，能够得到情况1的煤体冲出最大初速度v0max，如下：

(22)

情况3，如图3(c)，nl=3，Vm=8abdp，情况3的巷道临界冲击能量Eu和情况2的冲出煤体最大初速度v0max，图3(c)为情况3的煤壁破坏范围示意图，计算结果如下：

(23)

由上式，能够得到情况2的煤体冲出最大初速度v0max，如下：

(24)

情况4，如图3(d)，nl=4，Vm=9abdp，情况4的巷道临界冲击能量Eu和情况3的冲出煤体最大初速度v0max，图3(d)为情况4的煤壁破坏范围示意图，计算结果如下：

(25)

由式(25)，能够得到情况3的煤体冲出最大初速度v0max：

(26)

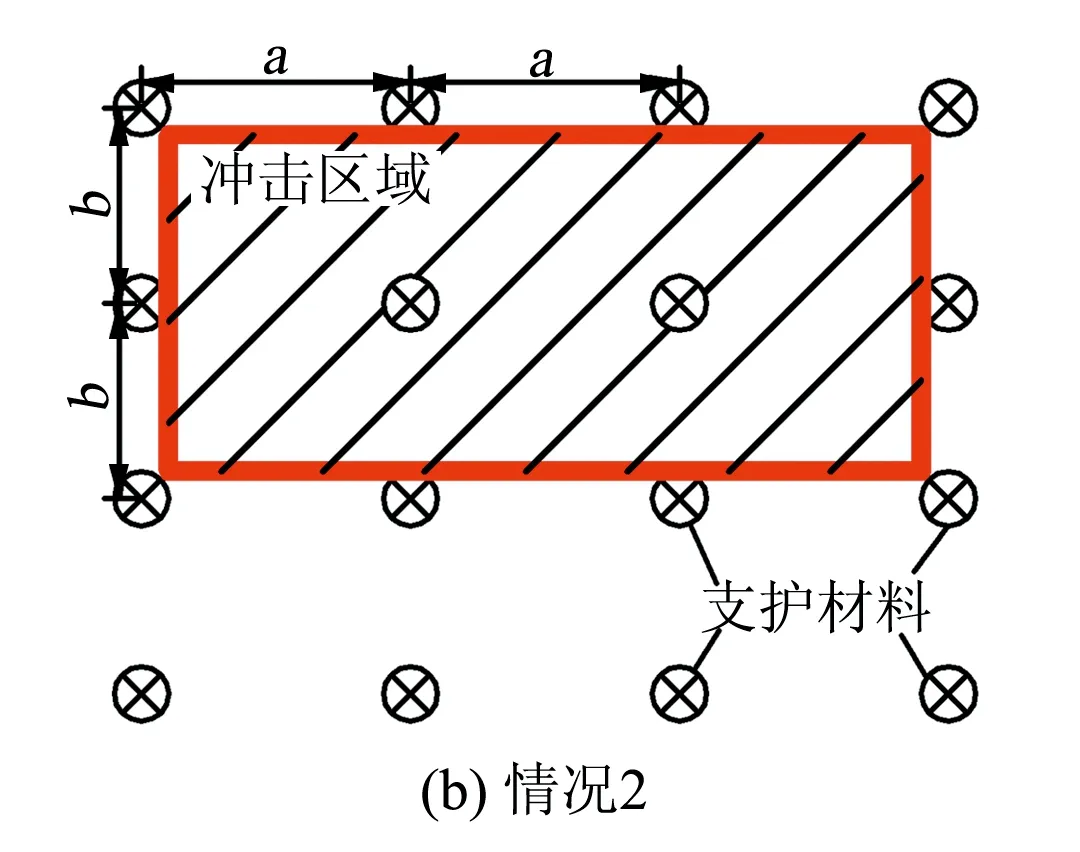
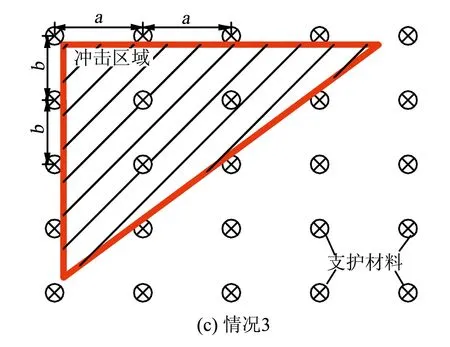
图3 不同范围的冲击地压发生示意

对强烈冲击地压进行讨论。这里的强烈冲击地压指的是巷帮或顶板整体发生冲击，冲出煤体数量较多的情况。此时，煤体冲出的初始速度v0可以通过如下过程进行计算。

古山煤矿多采用直墙半圆拱形巷道，巷高H为3.5m，巷宽D为4.7m，考虑到巷道上部为拱形，计算中煤壁的高度取2.5m。对于巷帮冲击地压，情况1是v0=0时，此时是巷帮强烈冲击发生的临界状态，用以计算临界冲击能量。情况2是煤壁1/2高度处煤体冲出至巷道中间位置时，可以认为巷道一半空间被充填，如图4(a)，此时每米巷道冲出煤体的体积为12.2m3，冲出煤体的碎胀系数取1.3，那么冲击煤体的深度dp为3.7m。情况3是煤壁1/2高度处煤体冲出至巷道另一端时，可以认为巷道约3/4的空间被充填，如图4(b)，同理可计算出此时冲击煤体的深度dp为5.55m。由此建立力学模型，求取煤体冲出的初始速度v0，如式(27)和式(28)。强烈冲击地压的冲出煤体深度大于锚杆长度2.2m，说明此时锚杆被整根冲出，其防冲效果较低。

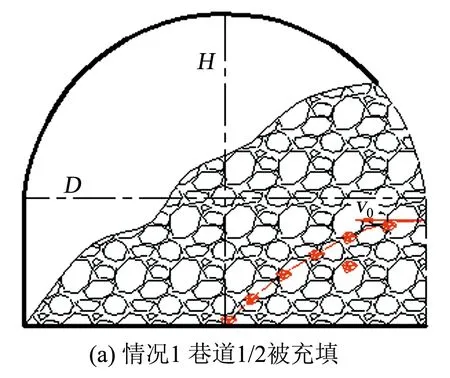
图4 巷帮冲击地压示意

(27)

(28)

由式(27)，(28)计算，得到巷帮冲击地压情况1的v0为6.65m/s，情况2的v0为13.3m/s。以此计算不同大小的外载能量导致的冲击地压强度。由式(19)，当v0=0m/s时，求得不同支护形式巷道发生强烈冲击地压的临界冲击能量；对于巷帮冲击地压，v0=6.65m/s时，求得巷帮冲击煤体将巷道1/2空间充填所需的外在能量；v0=13.3m/s时，求得巷帮冲击煤体将巷道3/4充填所需的外载能量。而对于顶板冲击地压，只要当煤体冲出即会对设备和人员产生较大伤害，因此仅对情况1，即v0=0m/s时，顶板强烈冲击发生的临界冲击能量进行计算。

强烈冲击地压发生的最小范围是帮部或顶板上单排支护材料及其周围煤岩体的冲出，由此能够算出发生强烈冲击的临界冲击能量。

以上是通过理论计算，探索各支护系统下不同类型冲击地压发生所需的能量，但是在现场实际中支护强度随时间降低或局部煤体较为破碎等原因均会导致冲击地压发生所需的能量有所减少。因此，为了将理论计算结果更加地符合实际，这里将理论计算结果乘以安全系数0.8。

2 各支护方案抗冲击能力计算

计算(方案一)全锚杆支护、(方案二)锚杆锚索联合支护和(方案三)全锚索支护的抗冲击能力。由模拟结果，提取各支护方案的煤壁附近的顶底板及两帮单位体积蕴藏弹性能数值的平均值，如表1所示。

表1 各支护方案下巷道不同位置的弹性能密度 J/m3

2.1 全锚杆支护抗冲击能力计算

2.1.1 计算参数

全锚杆支护设计：锚杆为φ22mm×2200mm，锚固长度不小于1000mm，间排距800mm×800mm，拉断载荷1.36×105N，弹性模量200GPa；每排锚杆13根，其中顶锚杆5根，左右两帮锚杆各4根。煤体：弹性模量4.0GPa，抗拉强度1.36MPa，密度1.3×103kg/m3。

2.1.2 抗冲击能力计算

由1.2节的理论推导，得到每根锚杆变形所消耗的能量为2.919×105J，每个锚杆断裂所消耗的能量为1.47×102J，单位体积的煤岩体破碎消耗的能量为2.31×102J。由表1可知，顶板及帮部支护系统的弹性能密度。

对于轻度冲击地压，将计算参数代入式(20)～(26)，可得到各种情况的抗冲击能力，结果详见表2。

表2 支护方案一抗轻度冲击能力计算

对于强烈冲击地压，计算情况1(强冲击发生的临界状态)、情况2(强冲击发生后1/2巷道被充填)、情况3(强冲击发生后3/4巷道被充填)所需的冲击能量。将计算参数代入式(19)，(27)，(28)，可得到各种情况的抗冲击能力，结果详见表3。

表3 支护方案一抗强烈冲击能力计算

2.2 锚杆锚索联合支护抗冲击能力计算

2.2.1 计算参数

锚杆锚索联合支护设计：锚杆为φ22mm ×2200mm，锚固长度不小于1000mm，间排距800mm×800mm，拉断载荷1.36×105N，弹性模量200GPa；每排锚杆13根，其中顶锚杆5根，左右两帮锚杆各4根。锚索：顶锚索规格为φ21.8mm×5.3m，帮锚索规格为φ21.8mm×4.3m，拉断载荷6.07×105N，弹性模量200GPa，每排3根或者4根，其中帮锚索2根，其余为顶锚索。煤体：弹性模量4.0GPa，抗拉强度1.36MPa，密度1.3×103kg/m3。

2.2.2 抗冲击能力计算

由1.2节的理论推导，得到每根锚杆变形所消耗的能量为2.919×105J，每个锚杆断裂所消耗的能量为1.47×102J；每根锚索变形所消耗的能量帮部为3.83×105J，顶部为6.38×105J，每根锚索断裂所消耗的能量帮部为7.03×103J，顶板为1.17×104J；单位体积的煤岩体破碎消耗的能量为2.31×102J。由表1可知顶板及帮部，以及支护系统的弹性能密度。

相对于全锚杆支护，锚杆锚索联合支护在抵抗强烈冲击地压的能力上有所提高。但是由于锚索是局部补强，而轻度冲击地压往往发生在巷道局部薄弱区域，因此锚杆锚索联合支护在抗轻度冲击的能力上与全锚杆支护一致，结果参照表2。

对于强烈冲击地压，由于冲击范围较大，锚索将会参与抗冲击能力的计算，计算情况1(强冲击发生的临界状态)、情况2(强冲击发生后1/2巷道被充填)、情况3(强冲击发生后3/4巷道被充填)所需的冲击能量，将计算参数代入式(19)，(27)，(28)，可得到各种情况的抗冲击能力，结果详见表4。

表4 支护方案二抗强烈冲击能力计算

2.3 全锚索支护抗冲击能力计算

2.3.1 计算参数

锚索：顶锚索规格为φ21.8mm×6.25m，帮锚索规格为φ21.8mm×4.3m，拉断载荷6.07×105N，弹性模量200GPa，每排13根，其中顶锚索5根，帮锚索4根。煤体：弹性模量4.0GPa，抗拉强度1.36MPa，密度1.3×103kg/m3。

2.3.2 抗冲击能力计算

由1.2节的理论推导，得到每根锚索变形所消耗的能量帮部为3.83×105J，顶部为6.45×105J，每根锚索断裂所消耗的能量帮部为7.03×103J，顶板为1.17×104J；单位体积的煤岩体破碎消耗的能量为2.31×102J。由表1可知，顶板及帮部，支护系统的弹性能密度。

对于轻度冲击地压，将计算参数代入式(20)～(26)，可得到各种情况的抗冲击能力，结果详见表5。

表5 支护方案三抗轻度冲击能力计算

对于强烈冲击地压，计算情况1(强冲击发生的临界状态)、情况2(强冲击发生后1/2巷道被充填)、情况3(强冲击发生后3/4巷道被充填)所需的冲击能量。将计算参数代入式(19),(27),(28)，可得到各种情况的抗冲击能力，结果详见表6。

表6 支护方案三抗强烈冲击能力计算

3 大倾角软煤巷道支护的抗冲击能力分析

依据上述理论计算结果，对各支护方案下巷道的抗冲击能力进行如下分析：

对于轻度和强烈冲击地压，全锚杆支护和锚杆锚索联合支护的巷道顶板和两帮的临界冲击能量、最大冲击速度均相差较小，表明了这两种支护形式下顶板和帮部的抗冲击能力相差较小，并且帮部和顶板的冲击速度也较为相似；但是全锚索支护巷道的顶板的临界冲击能量是帮部冲击能量的近2倍，表明了这种支护形式对于顶板冲击的抵抗能力要远大于帮部冲击。由图2可知，古山煤矿巷道围岩内静载弹性能主要位于顶底板内，也就是说顶底板所需要承受的冲击载荷会远大于巷道两帮，说明了全锚索支护更符合古山煤矿的原岩应力及地质条件。

对于轻度冲击地压，随着发生范围的逐渐增大，引发冲击地压的临界能量在不断增大，而最大冲击速度逐渐降低，表明范围越大的轻度冲击地压，支护结构对其的抵抗能力越强，且其发生强度越低。

对3种支护方案进行纵向比较可知，随着支护强度的增大，发生冲击时煤体最大的冲出速度也相应地增大，表明了支护强度的增大能够更好地阻止冲击地压地发生，但是一旦冲击发生，冲击的强度也会相应增大。巷道同一位置对轻度冲击地压的抵抗能力大小的排序是“全锚杆支护=锚杆锚索联合支护<全锚索支护”；而对强烈冲击地压的抵抗能力大小的排序是“全锚杆支护<锚杆锚索联合支护<全锚索支护”，表明了3种支护方案中全锚索支护抗冲击能力最强。