基于GIS的路网应急疏散脆弱性研究
2019-03-29姜文秦其明
姜文, 秦其明
(1.北京大学地球与空间科学学院遥感与地理信息系统研究所,北京 100871; 2.空间信息集成与3S工程应用北京市重点实验室,北京 100871; 3.地理信息基础软件与应用国家测绘地理信息局工程技术研究中心,北京 100871)
0 引言
城市道路交通系统是分布区域广泛的网状系统,该网状系统的运行状态对灾害的抵抗能力不强,灾害发生的种类和频率会随着城市规模的增大和现代化程度的增高而增加。因此,对路网应急疏散问题的研究受到国内外的广泛关注。应急疏散主要为了解决当发生灾害时,危险地区的人们如何尽快转移到安全区域的问题。作为一个整体的交通运输网,牵一发而动全身,往往一个“瓶颈”路段的交通堵塞就能导致整个交通运输网的瘫痪从而影响应急疏散。因此,开展城市交通路网脆弱性研究对城市应急疏散具有重要意义,同时可以通过确定和分析城市交通路网的脆弱点来衡量其通行能力。
考察路网疏散方面的研究开始于20世纪70年代,Houston提出了最早用于疏散分析的疏散率模型[1](dissipation rate model)和用于估算疏散时间的简单统计公式; 随后,Voorhess和Sheffi等也相继提出了应急疏散的各种模型[2-4],并在不同的条件下进行了应用。对于应急疏散脆弱性分析,国内开展的相关研究更晚些,大多从路网应急疏散路径选择、人员应急疏散行动的决策行为和公路交通应急物资运输保障等方面开展研究[5-7]。刘小明等[8]指出国内外应急疏散理论与技术研究关键之一是如何在有效的时间内,将事故发生地点集结的待疏散车辆尽快疏散到安全区域; 宋永朝等[9]运用最小费用最大流理论建立了局域路网疏散分配模型,通过查找最小截量组成弧的分布位置,并对路网中最小截量组成弧的容量进行改造,进而有效提高局域路网的应急疏散能力; 尹洪英等[10]对路网脆弱性的评估方法进行了分类。可以看出,目前应急疏散脆弱性分析方向的研究,多偏向于在数学和运筹学领域开展。地理信息系统(GIS)具有强大的空间信息分析功能,能够直观地展示空间分布模式和发展趋势,比传统学科更有利于开展交通路网脆弱性研究。
本文为了弥补传统的数学和运筹学方法的不足,充分发挥GIS在空间分析领域的技术优势,提出了结合最小费用最大流(minimal cost maximal flow,MCMF)算法搭建GIS平台来寻找具体交通路网网络模型脆弱点、分析路网脆弱性的新方法。首先,构建了应急疏散路网模型,并在各路段容量有限的条件下,以疏散交通个体数量最多和总疏散时间成本最小为目标,利用最短路径快速算法(shortest path faster algorithm,SPFA)计算路网系统容量; 其次,在此模型基础上,获取限制路网系统疏散能力的“瓶颈路段”,指导路网容量的提升,降低路网应急疏散的脆弱性。基于上述理论分析,搭建了寻找具体交通路网网络模型脆弱点的GIS平台,运用修正模型方法模拟建立了某实地及其周围地区的路网疏散分配模型; 最后,将该模型在GIS平台上进行了试验,准确找到路网的脆弱之处,同时还得到了在路网最大流时,疏散时间最短的流量分布。将道路网扩容前后的路网容量进行对比,证实应急疏散脆弱性分析的必要性和有效性。
1 应急疏散路网模型构建
1.1 路网容量定义
路网容量分为狭义与广义路网容量。前者指单位时间内城市道路网可通行的最大车流量或人流量,后者为一定的时间段内,在各种条件的约束下,城市道路网上可容纳的行人或交通个体数; 对于外部约束条件来说,路网容量可分为环境容量Cev、物理容量Cph和经济容量Cec,这3类容量彼此独立存在,同时影响着城市道路网容量,不计其他因素影响,则在外部条件的制约下,城市交通广义容量为C=min(Cph,Cev,Cec)。本文从狭义路网容量角度,分析局部(区域)道路网在一定服务水平下所能承担的最大交通容量,即允许通行的最大人流量。
1.2 应急疏散路网模型
灾害事件发生时,如何在最短时间内通过疏散路径从危险区到达安全区是人们关心的,所以应急疏散路径选择的优先考虑条件是总路径疏散时间最小。这里从网络及网络流和路网应急疏散的交通分配2方面来建立应急疏散路网模型。
定义一个网络:N=(V,E,c,X,Y),其中V为该网络图的顶点集;E为有向边(即弧)集;c为弧上的容量;X与Y分别为发点集与收点集。如果满足以下条件: ①G=(V,E)是一个有向图; ②c(e)是边e的容量,为E上的非负函数,定义为容量函数; ③X与Y分别为G的发点集与收点集,二者是V的2个非空且不相交子集,I=V(X∪Y)称为G的中间点集。X的顶点称为发点(源),Y的顶点称为收点(汇),I的顶点称为中间点。若|X|=1,|Y|=1,称N为单源单汇网络,如图1所示。

图1 单源单汇网络图Fig.1 Single source-single terminal network
若|X|>1,|Y|>1,称N为多源多汇网络,如图2所示。

图2 多源多汇网络图Fig.2 Multisource-multiterminal network
设N为一个网络,f是E上的非负函数,如果:
1)容量限制条件
0≤f(e)≤c(e),∀e∈E
;
(1)
2)流量守恒条件
(2)
式(1)表示通过该边的流量不能超过该边的容量。式(2)中,N+(v)为过v的所有出弧的集;N-(v)为v的所有入弧的集;f为网络N的一个流;f(e)为边e的流量。每个中间点流进的流量等于流出的流量,中间点流量保持平衡。值得注意的是,任一网络至少存在一个流,如零流(f(e)=0,e∈V)。图2表示一个网络及网络流,它的发点集为X={x1,x2}; 收点集为Y={y1,y2}; 中间点集为I={v1,v2,v3,v4}。
1.2.1 路网模型构建
城市道路交通网都可看作一个赋权有向图。图中的结点代表实际问题中的道路交叉口(包括高架桥的出入口),图中的边代表相邻结点之间的道路。一般情况下,可将边的权重归结为路的宽度、长度和拥塞程度等其他因素; 而灾时疏散过程中,与空间距离和运输费用相比较,人们更关注疏散所需的时间,因此本文将道路的通行时间作为路网模型中边的权重。
依据灾害事件的类型及其影响范围,路网疏散问题可分为点事件和面事件[11]。无论是建筑物内疏散还是露天大范围疏散,都可以转化为疏散网络的问题,本文的应急疏散脆弱性分析主要以网络流优化为基础,疏散的优化目标是发挥整个路网交通系统的最大效率[12]。点事件的路网疏散分配问题可视为单源单汇或单源多汇问题; 面事件的路网疏散分配问题可视为多源多汇问题。
1.2.2 路网模型简化
实际研究中,可将单(多)源多汇网络转换成一个单源单汇网络。在解决实际问题时,常采用这种方法,假设每条边的容量无限,于多个发点前添加一个发点s,多个收点后添加一个收点t,如图3所示。

图3 多源多汇网络的转化Fig.3 Transformation of multisource- multiterminal network
1)V′=V∪{s,t} ,
(3)
式中s和t分别为N′的发点与收点;
2)E′=E∪{(s,t)|x∈X}∪{(y,t)|y∈Y} ;
(4)
3)c′=c(e),e∈E;c′(s,x)=,x∈X,
c′(y,t)=,y∈Y。
(5)
2 应急疏散脆弱性分析算法
2.1 最大流最小割定理及增广链
最大流最小割定理:
1)设f是流,K是割,若Valf=C(K),则f是最大流,K是最小割。
2)网络N的最大流的流量等于最小割的容量。
该定理是图论的重要核心,在适当的选择网络后,应用这个定理往往能够获得解决。从该定理的证明中,可以引出求网络最大流的一个算法。但这种方法实际做起来有困难,因为没解决如何寻找增广链的问题。
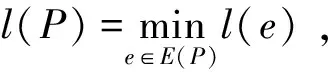
(6)
若l(P)=0,则称P链为饱和链; 若l(P)>0,则称P链为非饱和链。
设f是一个流,P是从源s到汇t的一条链,若P满足: ①在弧e∈P+上,0 ≤f(e) 一般的网络最大流算法没有考虑到网络上产生最大流的费用问题,费用因素在许多实际问题中也占有很重要的地位。对于应急疏散问题将疏散时间作为路径费用,必须在保证路网流量一定的情况下,尽可能缩短疏散时间。因此需要求解网络的最小费用最大流问题。 求最小费用最大流常采用求最短路径的SPFA算法,该算法能够处理负边,能在O(kE)的时间复杂度内求出源点到其他所有点的最短路径。 设Fee代表s到i点的当前最小费用,Pred代表s到i的当前最短路径中i点之前的一个点的编号。开始时Dist全部为+∞,只有Dist[s]=0,Pred全部为0。 建立一个队列,将所有需要迭代的点存入队列,初始时队列中只有一个点s。用一个布尔数组记录并判断每个点是否处在队列中。每次迭代,取出队头的点v,依次枚举从v出发的边v→u,设边的费用为fee,判断Fee[v]+fee是否小于Fee[u],若小于则改进Fee[u],将Pred[u]记为v,并且由于s到u的最小费用变小了,有可能u可以改进其他的点,所以若u不在队列中,就将它放入队尾。就这样一直进行迭代,直到队列变空,也就是s到所有的最短距离都确定下来,结束算法,流程如图4所示。 图4 SPFA算法流程Fig.4 Flow chart of SPFA algorithm 本文选用北京市某区域的路网信息作为实验数据。该区域如图5所示,周边配套设施完整,幼儿园、中小学、大学、综合商场、医院、邮局、银行、宾馆公园等均有,是个典型的社区。从路网结构上分析,2条主干道相邻,支路分布均匀,但存在断头路。这些断头路势必会影响某个路段或交叉口的通行能力,影响整个路网容量的增加,从而影响应急疏散的效率。 图5 北京市某区域及其周围路网分布Fig.5 Distribution of road network in a region of Beijing 对照该卫星地图的二维地图,运用ArcGIS软件对其路网进行矢量化操作,得到初始路网,导入要素集,再进行拓扑检查,从而得到路网模型如图6所示。 图6 应急疏散路网模型Fig.6 Road network model of emergency evacuation 假设突发灾害事件发生在结点1和结点2,此次分析的路网是多源多汇型,利用修正模型法将其转化为单源单汇型。由于该小区及其周围路网属于局域路网,且本文选择了狭义的路网容量,即城市道路网单位时间内可以通行的最大的人流量或者车流量,而路网为社区路网,选取人为要疏散的交通个体,因此路网容量为每条路每分钟所能疏散的人的数量。根据路段长度大致估算路段的容量,由于社区街道相对较窄,假设一条路并排可以容纳4人,前后相距为1 m,算出每条道路上可以容纳的人数,并假设每条道路上所容纳的人数在1 min中内疏散完全; 路段上的时间消耗为路段长与速度之比,取人群疏散的平均速度为1 m/s; 然后把每条弧段的起点,终点补充好,至此,路网建立完毕。图中每条弧段的标注为(路网容量和时间费用),路网容量单位为个/min,时间费用单位为min。 本文采用ArcEngine二次开发,实现的功能是将符合条件的路网数据加载,进行道路网的脆弱性分析: MCMF及其脆弱性分析。首先,路网数据必须包含4个字段,分别是: content(短整型)——容量、fee(双精度)——时间费用、start_vex(短整型)——开始结点、end_vex(短整型)——结束结点; 其次,该路网是要经过拓扑检查,确定各个交叉口道路选择的灵活性。 3.2.1 系统设计及结果计算 系统界面包括菜单栏、工具栏、窗口显示栏和状态栏4大部分,如图7所示。 图7 系统界面设计图Fig.7 Design diagram of system interface 系统主要实现的功能是MCMF计算,最小费用时的流量分布和找出路网的脆弱之处; 辅助功能有查看图层属性和修改图层符号等。 将图6建立的路网数据加载进入GIS平台,分别点击“最小费用最大流”和“脆弱性分析”,运行结果如图8所示。图8中的最小费用计算结果指的是2 637个人平均的疏散时间为16.361 min; 高亮部分是路网中的饱和弧,即路网系统疏散能力的“瓶颈路段”,对该组成弧进行扩容处理,就能达到改造少量路段,有效增大路网容量,提高该社区路网应急疏散能力的效果。图9为MCMF下的流量分布。 (a) 流量分布(b) 脆弱性分析 图8流量分布与脆弱性分析 Fig.8Flowdistributionandanalysisofvulnerability 图9 MCMF下的流量分布Fig.9 Flow distribution under minimal cost maximal flow 由图9的流量标注中可以看出,图8中高亮部分的流量都已达到饱和值,为该小区应急疏散的脆弱之处。每条弧段的标注为(路网容量和实际流量)。 3.2.2 模拟计算结果 为了证实系统的可靠性,本文用运筹学的观点求解了该区域及其周围路网的最大流及最小时间费用下流量的分布情况,并进行验证。管理运筹学软件2.5版,是《管理运筹学》[13]的随书软件。该软件的模块有线性规划、最短路径、最小费用最大流等共15个子模块。本文采用最小费用最大流模块进行模拟,由运行的结果可知,最大流为2 637,和3.2.1节计算的结果完全契合,不仅如此,在最小时间费用最大流情况下的流量分布也完全契合。由此可以证明,上文搭建的GIS平台非常可靠,且图文一体,直观快捷。 3.2.3 道路网络优化效果分析 对3.2.2节中计算所得的路网瓶颈扩容一倍,扩容之前与扩容之后的最大流量与平均时间费用如表1所示。 表1 道路网扩容前后情况对比Tab.1 Minimal time cost and maximal flow before and after road network expansion 由表1可以看出,尽管平均疏散时间减少得不明显,但是扩容之后路网的最大流扩大了将近一倍。由此可以看出,图9中找到的道路瓶颈确实阻碍了整个路网容量的增加,该路段也就是路网改造的关键之处。 本文充分发挥了GIS在空间分析领域的技术优势,提出了结合最小费用最大流(MCMF)算法搭建GIS平台来寻找具体交通路网网络模型脆弱点,分析路网脆弱性的新方法。通过实际算例分析,以最大流-最小割,最小费用最大流和GIS相结合的方法,对北京市某区域进行了应急疏散脆弱性分析,找到了路网的脆弱地方,通过处理路网的这些“瓶颈之处”,就能在改造少量路段的条件下,实现有效增大路网容量的目的,从而提高路网的应急疏散能力。主要结论如下: 1)路网容量和费用方面。本文中疏散的对象是人,费用为疏散时间,但搭建的GIS平台的功能并不局限于此。从大的范畴来讲,疏散的对象是交通个体,费用可以为金钱时间等其他疏散成本。 2)路网建模方面。选取的实例为多源多汇网络,而多源多汇网络可转化成单源单汇网络,且点事件的路网疏散分配问题为单源单汇或单源多汇问题,面事件的路网疏散分配问题为多源多汇问题,因此,此路网模型可以涵盖路网疏散问题的两大事件: 点事件和面事件,应用性比较强。 3)脆弱性分析方面。本文方法不仅能够找到整个疏散路网的瓶颈之处,还能计算出基于最小时间的最大流在各个路段上的分布,可给实际疏散工作提供数据支持和决策辅助。 4)扩容前后对比方面。对于“瓶颈路段”的扩容,能够显著增加路网容量,减少路网的脆弱性。2.2 MCMF算法

3 实验与结果

3.1 路网建立

3.2 基于GIS的应急疏散脆弱性分析



4 结论
