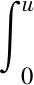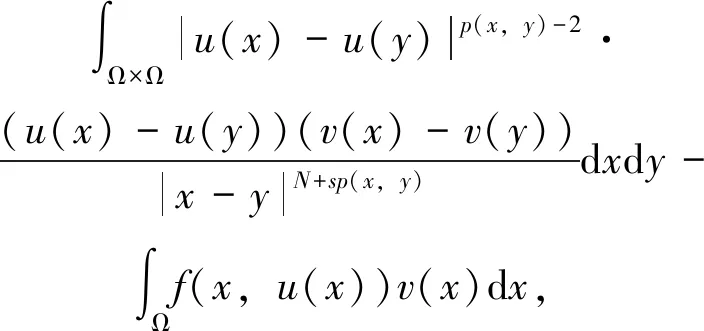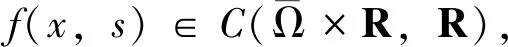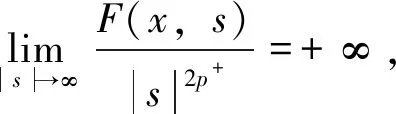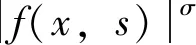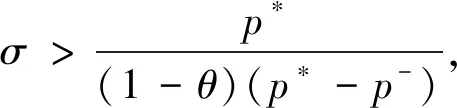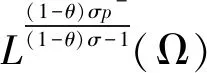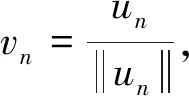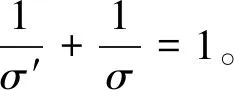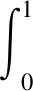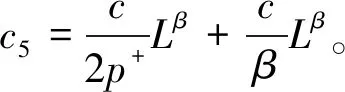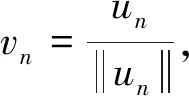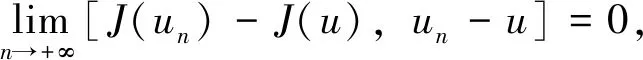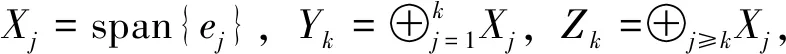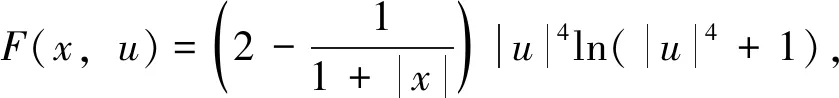一类分数阶基尔霍夫方程的无穷多解*
2019-03-29张申贵
张申贵
(西北民族大学数学与计算机科学学院, 甘肃 兰州 730030)
在研究弹性弦自由振动问题时,德国物理学家Kirchhoff 推广了经典的达朗贝尔波方程,并建立了如下形式的方程
(1)
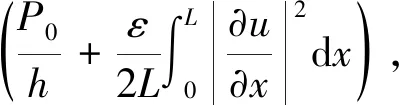
(2)
其中a,b为正常数。该方程可以更加精确的描述细菌在特定区域内的传播过程,u表示种群密度, 参见文献[1],其对应的稳态方程为
(3)
近年来, 学者们开始利用变分方法和临界点理论研究问题(3)的可解性[2-8]。另外, 在文献[9]中, Fiscella 和 Valdinoci 研究了一类分数阶基尔霍夫模型, 并且详细地讨论了分数阶基尔霍夫型方程的物理意义。本文中, 利用临界点理论研究分数阶基尔霍夫方程 Dirichlet 边值问题
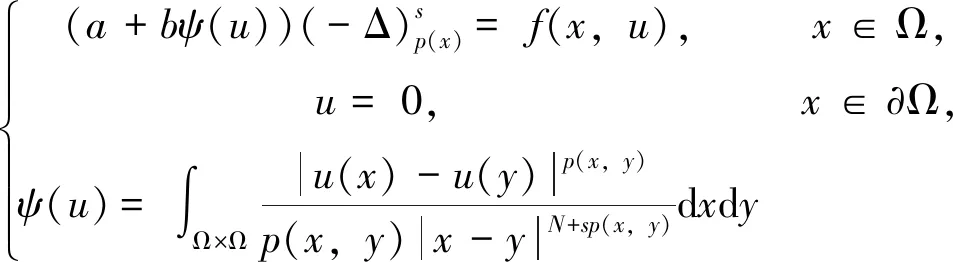
(4)
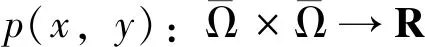
设0 本文中,在不同于(AR)的超线性条件下, 我们将利用临界点理论中的喷泉定理[19]得到问题(4)无穷多高能量解的存在性定理。 变指数分数阶Sobolev 空间的性质, 见文献[20-21]。 其中S(Ω)为可测的实值函数集合,其范数为 |u|Lq(x)(Ω)=|u|q(x)= 记变指数分数阶Sobolev 空间为 [u]s,p(x,y)= 引理2[20]线性有界算子J定义为: ∀u,v∈W0 引理4[19](喷泉定理)设X为Banach空间,X=Zk⊕Yk,dimYk<+∞。若泛函I∈C1(X,R),满足:I(0)=0,I(u)=I(-u),且 (i)泛函I满足(C)条件,即 对任何点列{un}⊂X,由{I(un)}有界,(1+||un||)||I′(un)||→0(n→+∞),蕴含{un}有收敛子列; 则泛函I有一列趋向于+∞的临界值。 称u∈W0是问题(4)的弱解指:对∀v∈W0,有 在W0上定义能量泛函I如下: 其中 则I∈C1(W0,R),且 [I′(u),v]=(a+bψ(u))· 则u∈W0是问题(4)的(弱)解等价于u是泛函I的临界点。 假设以下条件成立: (F3) 设F(x,0)=0,F(x,s)=F(x,-s),对所有x∈Ω和s∈R成立。 本文的主要结果如下: 定理1 设条件(F0) (F1) (F2)和(F3)成立,则问题(4)有一列解{uk}k∈N满足:当k→+∞时,有I(uk)→+∞。 证明下面利用喷泉定理(引理 4)证明定理 1。 第1步证明泛函I满足(C)条件。设{un}⊂W0为能量泛函I的(C)序列,那么 |I(un)|≤c3,(1+||un||)||I′(un)||≤c3 (5) 首先,证明{un}在空间W0中有界,反设{un}在W0中无界,则当n→+∞时,有 (6) (7) 利用Hölder不等式和式(7),有 (8) (9) 所有x∈Ω和u∈R成立。由条件(F0),(F2),式(9),有 (10) (11) 结合式(10),式(11),有 (12) 由式(6),式(12),当n→+∞时,有 (13) 结合式(8),式(13),当n→+∞时,有 (14) 当n充分大时,利用条件(F2),式(11),有 (15) (16) [I′(un),un]= (17) 由式(5),式(6),式(16),式(17),当n→+∞时,a≤0,这与a>0矛盾,故{un}在W0中有界。 注意到W0是自反的 Banach 空间,则存在u∈W0,使得{un}在W0中弱收敛于u,且{un}在Lβ(Ω)中强收敛于u,其中p-≤β (18) ∀u,v∈W0 由引理 2,{un}在W0中强收敛于u,故泛函I满足条件(C)。 记γk= sup{|u|β:u∈Zk,|u|=1},其中|u|β为Lβ(Ω)的范数,则当k→+∞时,有γk→0[20]。 对于 由式(9)和引理1,有 第3步证明泛函I满足引理4中条件(iii)。 由条件(F1)和式(9),对于∀ϑ>0,存在c7>0,使得 (19)
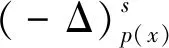
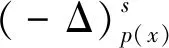
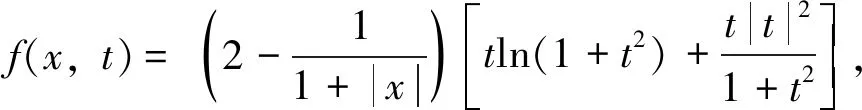
1 准备知识
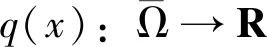
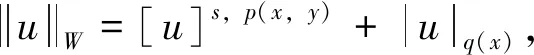
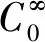
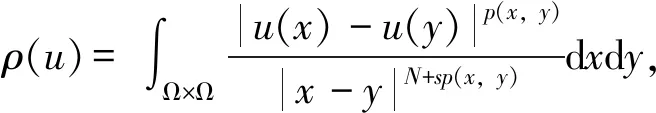
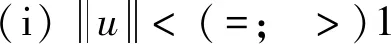
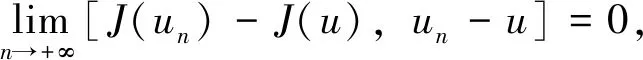
2 主要结果